Heat Transfer by Convection

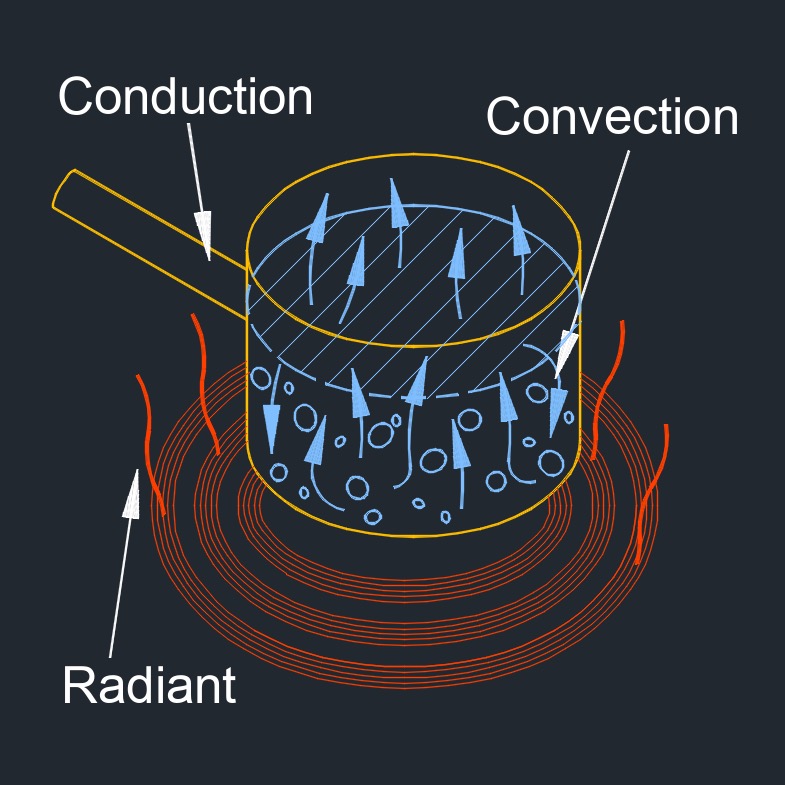Heat transfer by convection, abbreviated as Q_c, also called heat convection or convective heat transfer, is the process of heat transfer that occurs when a fluid (such as a gas or a liquid) is in motion and heat is transferred from one point to another due to the movement of the fluid.  This type of heat transfer occurs primarily in fluids and is caused by the flow of the fluid.  When a fluid is heated, it expands and becomes less dense, causing it to rise.  This movement of the fluid creates a flow that carries heat from one location to another.

Convection can occur naturally, such as in the case of hot air rising from a heater, or it can be forced, such as in the case of a fan blowing air over a hot surface.  The transfer of thermal energy can occur through three modes of heat transfer: conduction, convection, and radiation.

There are two types of convecion: natural convection and forced convection.  Natural convection is fluid flow caused by changes to the fluid, such as change of density or temperature variations of the fluid.  Forced convection is convection that is caused by a a piece of equipment, such as a pump or a fan.

Heat Transfer by Convection Formula
\(  Q_c \;=\;  h \cdot A_c \cdot (T_h - T_c) \)     (Heat Transfer by Convection) \( h  \;=\; \dfrac{ Q_c }{ A_c \cdot ( T_h - T_c) }\) \( A_c  \;=\; \dfrac{ Q_c }{ h \cdot ( T_h - T_c ) }\) \( T_h  \;=\; \dfrac{Q_c }{ h \cdot A_c }  + T_c \) \( T_c  \;=\; T_h -  \dfrac{Q_c }{ h \cdot A_c } \)
Symbol	English	Metric
\(\large{ Q_c }\) = Heat Transfer by Convection	\(Btu\;/\;hr\)	\( W \)
\(\large{ h }\) = Heat Transfer Coefficient	\(Btu\;/\;hr-ft^2-F\)	\(W\;/\;m^2-K\)
\(\large{ A_c }\) = Area Cross-section	\( in^2 \)	\( mm^2 \)
\(\large{ T_h }\) = Higher Temperature	\( F \)	\( K \)
\(\large{ T_c }\) = Cooler Temperature	\( F \)	\( K \)

 

Heat Transfer by Convection Formula
\(  Q_c \;=\; h \cdot A \cdot \left( T_s - T_\infty \right) \)     (Heat Transfer by Convection) \( h  \;=\;  \dfrac{ Q_c }{ A \cdot ( T_s - T_\infty )  }\) \( A  \;=\;  \dfrac{ Q_c }{ h \cdot ( T_s - T_\infty ) }\) \( T_s  \;=\; \dfrac{ Q_c }{ h \cdot A}  + T_\infty \) \( T_\infty  \;=\; T_s -  \dfrac{ Q_c }{ h \cdot A} \)
Symbol	English	Metric
\(\large{ Q_c }\) = Heat Transfer by Convection	\(Btu\;/\;hr\)	\( W \)
\(\large{ h }\) = Heat Transfer Coefficient	\(Btu\;/\;hr-ft^2-F\)	\(W\;/\;m^2-K\)
\(\large{ A }\) = Surface Area	\( in^2 \)	\( mm^2 \)
\(\large{ T_s }\) = Surface Temperature	\( F \)	\( K \)
\(\large{ T_\infty }\) = Fluid Temperature	\( F \)	\( K \)

 

Heat Transfer by Convection Formula
\( Q_c \;=\; 4.5 \cdot cfm \cdot \Delta H \)     (Heat Transfer by Convection) \( cfm \;=\; \dfrac{ Q_c }{ 4.5 \cdot \Delta H }\) \( \Delta H \;=\; \dfrac{ Q_c }{ 4.5 \cdot cfm }\)
Symbol	English	Metric
\(\large{ Q_c }\) = Heat Transfer by Convection	\(Btu\;/\;hr\)	\( W \)
\(\large{ cfm }\)  = Cubic Feet per Minute	\(ft^3\;/\;min\)	\(m^3\;/\;min\)
\(\large{ \Delta H }\)  = Enthalpy Differential	\(Btu\;/\;lbm\)	\(kJ\;/\;kg\)