Heat Transfer by Conduction Formula |
||
|
\( Q_c \;=\; \dfrac{ k \cdot A_c \cdot (T_h - T_c) }{ d }\) (Heat Transfer by Conduction) \( k \;=\; \dfrac{ Q_c \cdot d }{ A_c \cdot (T_h - T_c) }\) \( A_c \;=\; \dfrac{ Q_c \cdot d }{ k \cdot (T_h - T_c) }\) \( T_h \;=\; \dfrac{ Q_c \cdot d }{ k \cdot A_c} + T_c \) \( T_c \;=\; T_h - \dfrac{Q_c \cdot d }{ k \cdot A_c} \) \( d \;=\; \dfrac{ k \cdot A_c \cdot (T_h - T_c) }{ Q_c } \) |
||
| Symbol | English | Metric |
| \(\large{ Q_c }\) = Heat Transfer by Conduction | \(Btu\;/\;hr\) | \( W \) |
| \(\large{ k }\) = Material Thermal Conductivity | \(Btu-ft\;/\;hr-ft^2-F\) | \(W\;/\;m-K\) |
| \(\large{ A_c }\) = Area Cross-section | \( in^2 \) | \( mm^2 \) |
| \(\large{ T_h }\) = Higher Temperature | \( F \) | \( K \) |
| \(\large{ T_c }\) = Cooler Temperature | \( F \) | \( K \) |
| \(\large{ d }\) = Thickness of the Material | \( in \) | \( mm \) |
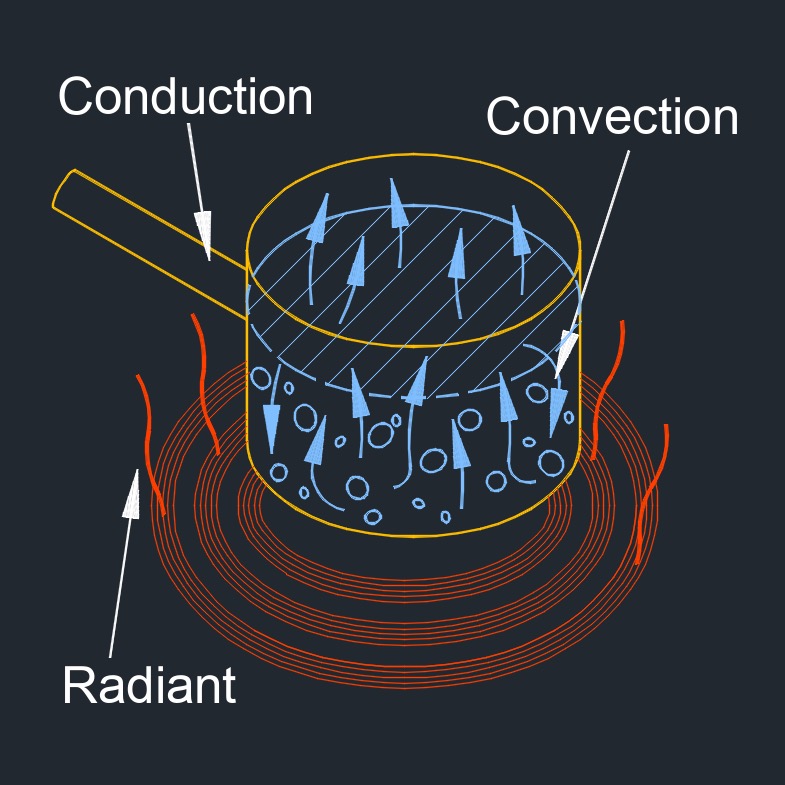
Heat transfer by conduction, abbreviated as Qc, also called heat conduction or conduction heat transfer, is a process of thermal energy transfer through a substance or between two objects in physical contact, where heat flows from a higher temperature region to a lower temperature region. This transfer occurs due to the temperature gradient or difference between the two regions, which causes the molecules in the higher temperature region to transfer some of their thermal energy to the neighboring molecules in the lower temperature region.
The rate of heat transfer by conduction depends on the thermal conductivity of the material, the thickness of the material, and the temperature difference between the two regions. The transfer of thermal energy can occur through three modes of heat transfer: conduction, convection, and radiation.
- See Article - Thermal Conductivity of Non-metallic Solids
Heat Transfer by Conduction Formula |
||
|
\( Q_c \;=\; \dfrac{ k \cdot A \cdot ( \frac{dT}{dx} ) }{ \Delta t }\) (Heat Transfer by Conduction) \( k \;=\; \dfrac{ Q_c \cdot \Delta t }{ A \cdot ( \frac{dT}{dx} ) }\) \( A \;=\; \dfrac{ Q_c \cdot \Delta t }{ k \cdot ( \frac{dT}{dx} ) }\) \( \frac{dT}{dx} \;=\; \dfrac{ Q_c \cdot \Delta t }{ k \cdot A }\) \( \Delta t \;=\; \dfrac{ k \cdot A \cdot ( \frac{dT}{dx} ) }{ Q_c }\) |
||
| Symbol | English | Metric |
| \(\large{ Q_c }\) = Heat Transfer by Conduction | \(Btu\;/\;hr\) | \( W \) |
| \(\large{ k }\) = Material Thermal Conductivity | \(Btu-ft\;/\;hr-ft^2-F\) |
\(W\;/\;m-K\) |
| \(\large{ A }\) = Surface Area | \( in^2 \) | \( mm^2 \) |
| \(\large{ \frac{dT}{dx} }\) = Temperature Gradient | \( F \) | \( K \) |
| \(\large{ \Delta t }\) = Time Interval | \( sec \) | \( s \) |