Heat Transfer Rate
Heat Transfer Rate Formula |
||
|
\( Q_t \;=\; k_t \cdot \dfrac{ \Delta T }{ l } \) (Heat Transfer Rate) \( k_t \;=\; \dfrac{ Q_t \cdot l }{ \Delta T }\) \( \Delta T \;=\; \dfrac{ Q_t \cdot l }{ k_t }\) \( l \;=\; \dfrac{ k_t \cdot \Delta T }{ Q_t }\) |
||
| Symbol | English | Metric |
| \( Q_t \) = Heat Transfer Rate | \(Btu\;/\;hr\) | \(W\) |
| \( k_t \) = Thermal Conductivity Constant | \(Btu-ft\;/\;hr-ft^2-F\) | \(W\;/\;m-K\) |
| \( \Delta T \) = Temperature Differential | \(F\) | \(K\) |
| \( l \) = Length or Distance | \(ft\) | \(m\) |
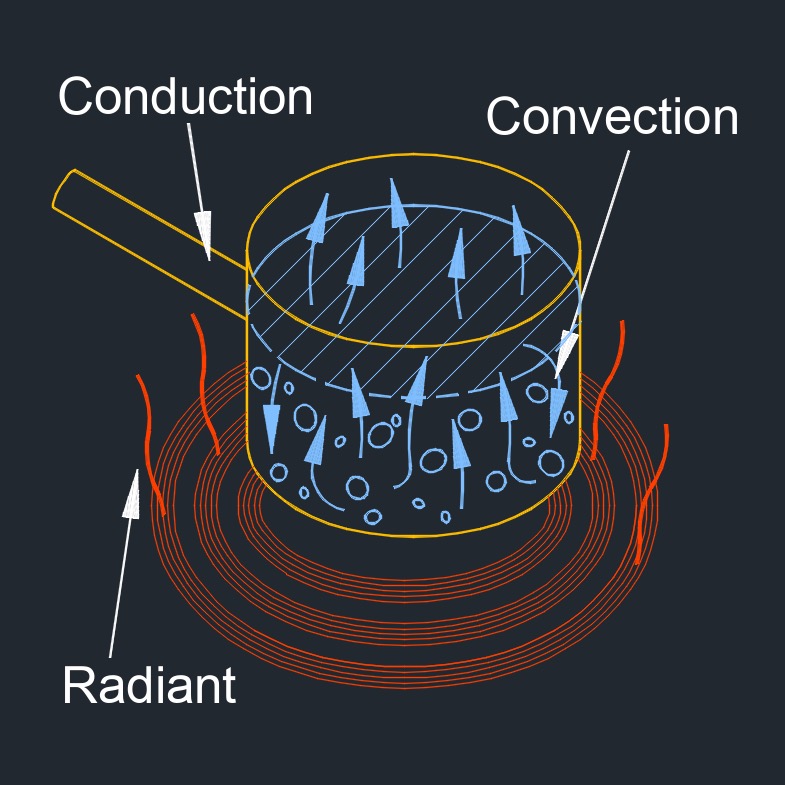
Heat transfer rate, abbreviated as \(Q_t\), refers to the amount of heat energy transferred per unit of time. It represents the rate at which heat is exchanged between two bodies or within a system.
In convection, the heat transfer rate is influenced by factors such as the convective heat transfer coefficient and the surface area over which heat transfer occurs. In radiation, the heat transfer rate is determined by the Stefan-Boltzmann law, which involves the emissivity and surface area of the objects involved. Understanding the heat transfer rate is crucial in various engineering applications, such as designing thermal systems, assessing heat exchanger performance, evaluating the efficiency of heating and cooling processes, and determining the heat dissipation capabilities of materials and devices.

