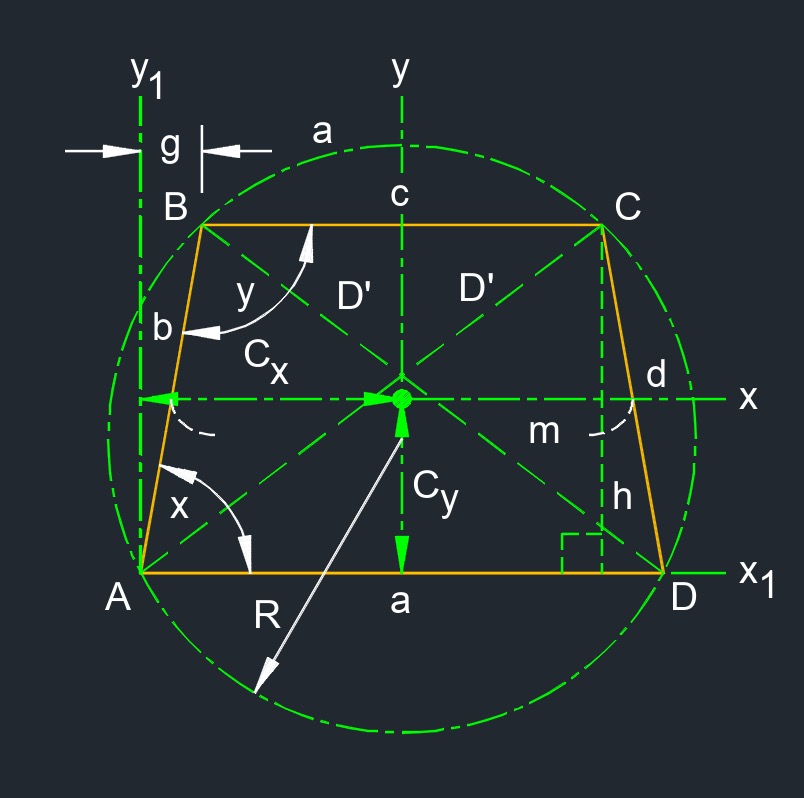
Plastic Section Modulus of an Isosceles Trapezoid formulas |
||
|
\( Z_x \;=\; \dfrac{ h \cdot \left( 2 \cdot c^2 - c\;a + 2 \cdot a^2 \right) }{ 12 } \) \( Z_y \;=\; \dfrac{ h^2 \cdot \left( 11 \cdot c^2 + 26 \cdot c \cdot a + 11 \cdot a^2 \right) }{ 48 \cdot \left( c + a \right) } \) |
||
| Symbol | English | Metric |
| \( Z \) = plastic section modulus | \( in^3 \) | \( mm^3 \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
