Law of Conservation of Mass Formula |
||
| \( \left( \dfrac{ \partial \rho }{ \partial t } \right) + (\; \nabla \cdot ( \rho \cdot v) \;) \;=\; 0 \) | ||
| Symbol | English | Metric |
| \( \partial \) = Infinitesimal Change | - | - |
| \( \rho \) (Greek symbol rho) = Density | \(lbm\;/\;ft^3\) | \(kg\;/\;m^3\) |
| \( t \) = Time | \( sec \) | \( s \) |
| \( \nabla \) = Divergence | - | - |
| \( v \) = Fow Velocity Field | \(ft\;/\;sec\) | \(m\;/\;s\) |
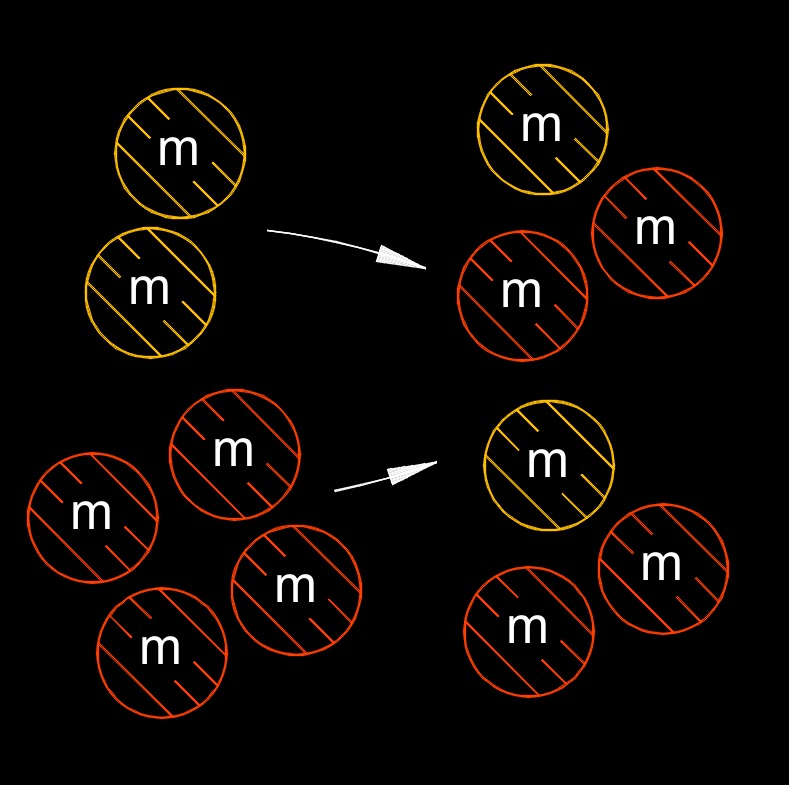Law of conservation of mass states in a closed system, the mass of the system cannot change over time. In other words, mass cannot be created or destroyed, it is conserved.
According to this law, in any physical or chemical process or interaction, the total mass of the reactants is equal to the total mass of the products. The atoms that make up the reactants rearrange themselves during the process, but the total number of atoms and their mass remains unchanged. This law is closely related to the principle of the conservation of atoms, which states that the number and types of atoms in a closed system also remain constant during a chemical reaction. This means that the total number of each type of atom in the reactants is equal to the total number of each type of atom in the products.
This law is a fundamental principle in stoichiometry, the branch of chemistry that deals with the quantitative relationships between reactants and products in chemical reactions. It forms the basis for balancing chemical equations and calculating the masses and quantities of substances involved in reactions. It's worth noting that in certain nuclear reactions or relativistic processes, where nuclear binding energies or energy mass equivalence is involved, there can be slight deviations from strict mass conservation. However, in everyday macroscopic chemical reactions, the law of conservation of mass is generally applicable and provides a fundamental understanding of mass transformations and interactions in closed systems.
