Lift Force Formula |
||
|
\( L \;=\; \dfrac{1}{2} \cdot C_l \cdot \rho \cdot v^2 \cdot A \) (Lift Force) \( C_l \;=\; \dfrac{ 2 \cdot L }{ \rho \cdot v^2 \cdot A } \) \( \rho \;=\; \dfrac{ 2 \cdot L }{ C_l \cdot v^2 \cdot A } \) \( v \;=\; \sqrt{ \dfrac{ 2 \cdot L }{ C_l \cdot \rho \cdot A } }\) \( A \;=\; \dfrac{ 2 \cdot L }{ C_l \cdot \rho \cdot v^2 } \) |
||
| Symbol | English | Metric |
| \( L \) = Lift Force | \( lbf \) | \(N\) |
| \( C_l \) = Lift Coefficient | \( dimensionless \) | \( dimensionless \) |
| \( \rho \) (Greek symbol rho) = Air Density | \(lbm \;/\; ft^3\) | \(kg \;/\; m^3\) |
| \( v \) = Air Velocity Related to Wing | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( A \) = Lift Surface Area | \( ft^2 \) | \( m^2 \) |
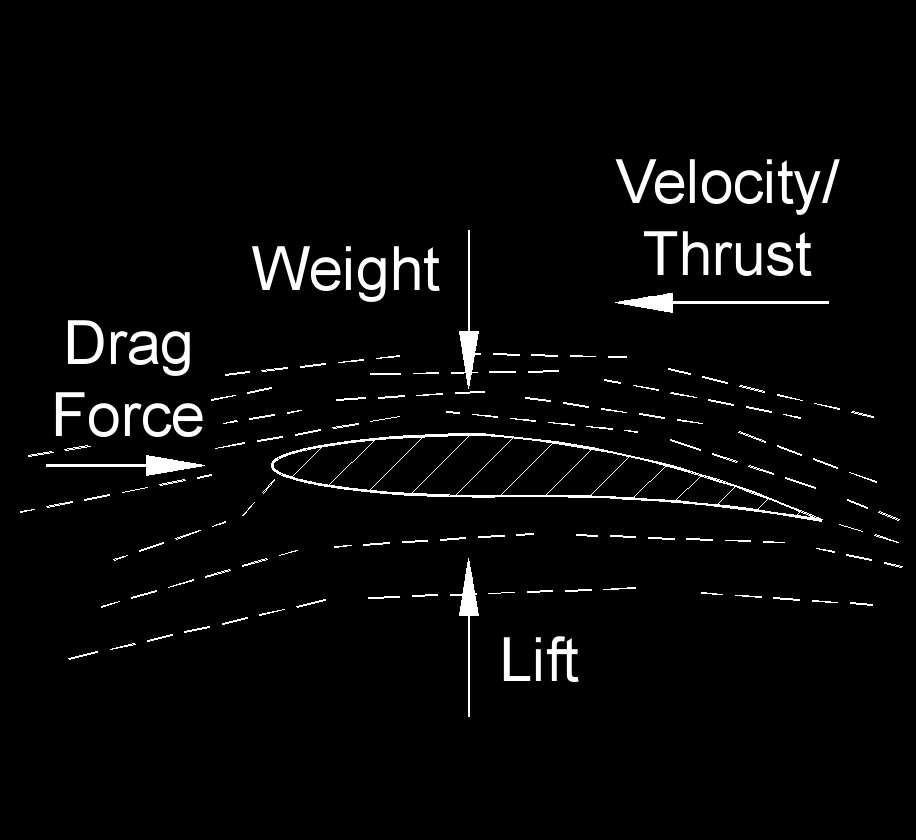Lift force, abbreviated as L, also called lift, for an body moving through a fluid (gas or liquid) or air, is the force exerted perpendicular to the direction of travel. It's a fundamental aerodynamic phenomenon that describes the force exerted on an object (such as an aircraft wing or a rotor blade) perpendicular to the direction of an oncoming fluid flow, typically air. Lift is what allows aircraft to generate upward motion and counteract the force of gravity.
Lift is primarily generated due to differences in air pressure on the upper and lower surfaces of a wing or airfoil. When an airfoil moves through the air at a non-zero angle of attack (the angle between the chord line of the airfoil and the oncoming airflow), it causes the air to flow over and under the airfoil, creating different pressure distributions.
The Bernoulli's principle, which relates the speed of a fluid flow to its pressure, helps explain the lift generation. As the air moves faster over the curved upper surface of the airfoil, its pressure decreases. Meanwhile, the slower-moving air beneath the airfoil has higher pressure. This pressure difference results in an upward force, perpendicular to the direction of the airflow, known as lift.
Key Points about Lift Force
- Lift is primarily generated due to the pressure difference above and below the wing. Faster airflow over the curved upper surface of a wing creates lower pressure compared to the slower airflow beneath, as explained by Bernoulli’s principle.
- The angle between the wing and the oncoming airflow significantly affects lift. An optimal angle maximizes lift, but too high an angle can cause a stall, where airflow separates from the wing, reducing lift.
- The design of the wing (airfoil) is critical. Its curved upper surface and flatter lower surface enhance the pressure differential, contributing to lift.
