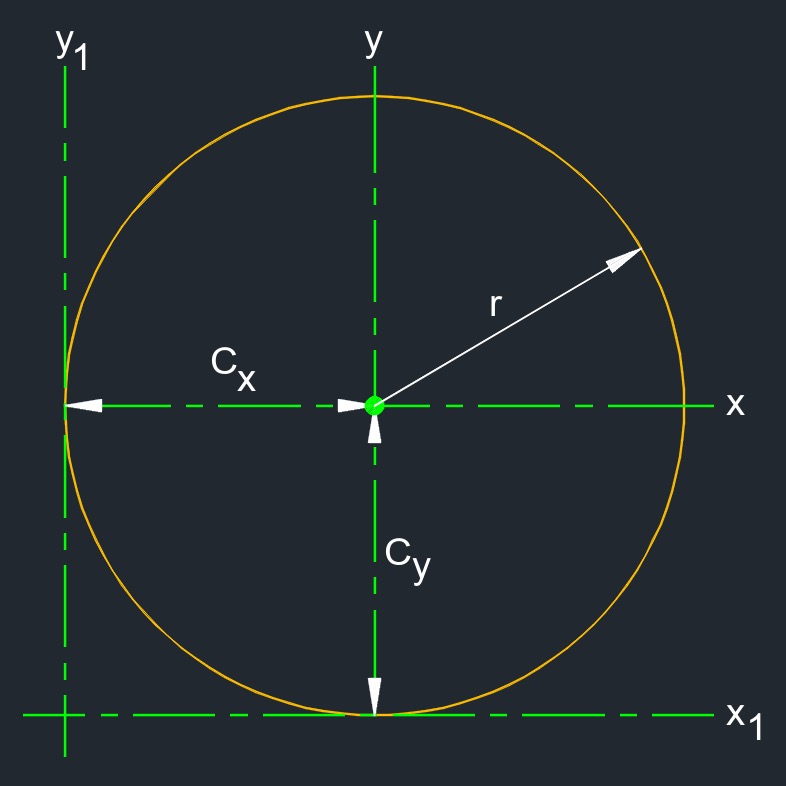
Second Moment of Area of a Circle
Second Moment of Area of a Circle formulas |
||
|
\( I_{x} \;=\; \dfrac{ \pi \cdot r^4}{ 4 }\) \( I_{y} \;=\; \dfrac{ \pi \cdot r^4}{ 4 }\) \( I_{x1} \;=\; \dfrac{ 5 \cdot \pi \cdot r^4}{ 4 }\) \( I_{y1} \;=\; \dfrac{ 5 \cdot \pi \cdot r^4}{ 4 }\) |
||
| Symbol | English | Metric |
| \( I \) = Moment of Inertia | \( in^4 \) | \( mm^4 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = Radius | \( in \) | \(mm \) |