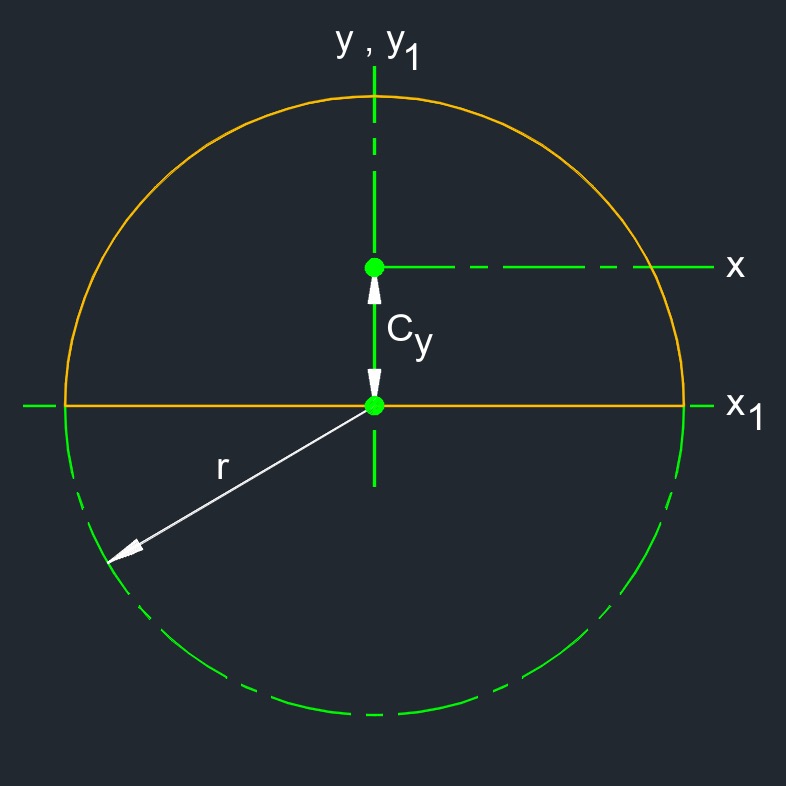
Radius of Gyration of a Half Circle formulas |
||
|
\( k_{x} \;=\; r \cdot \sqrt{ \dfrac{1 }{ 4 } - \dfrac{ 16 }{ 9 \cdot \pi^2 } } \) \( k_{y} \;=\; \dfrac{ r }{ 2 }\) \( k_{z} \;=\; r \cdot \sqrt{ \dfrac{ 1 }{ 2 } - \dfrac{ 16 }{ 9 \cdot \pi^2 } } \) \( k_{x1} \;=\; \dfrac{ r }{ 2 }\) \( k_{y1} \;=\; \dfrac{ r }{ 2 }\) \( k_{z1} \;=\; \dfrac{ \sqrt {2} }{ 2 } \cdot r \) |
||
| Symbol | English | Metric |
| \(\large{ k }\) = radius of gyration | \( in \) | \( mm \) |
| \(\large{ \pi }\) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \(\large{ r }\) = radius | \( in \) | \( mm \) |
