Wetting Perimeter of a Circular Pipe Formula |
||
|
\( P_w \;=\; \left(\; cos^{-1} \left( 1 - \dfrac{ h }{ r } \right) \; \right) \cdot d \) (Wetted Perimeter of a Circular Pipe) \( h \;=\; r \cdot \left( 1 - cos \left( \dfrac{ P_w }{ d } \right) \;\right) \) \( r \;=\; \dfrac{ 1 - cos \left(\dfrac{ P_w }{ d } \right) }{ h } \) \( d \;=\; \dfrac{ P_w }{ cos \left( 1 - \dfrac{ h }{ r } \; \right) }\) |
||
| Symbol | English | Metric |
| \( P_w \) = Wetting Perimeter | \( in \) | \( mm \) |
| \( h \) = Fluid Depth | \( in \) | \( mm \) |
| \( r \) = Inside Radius | \( in \) | \( mm \) |
| \( d \) = Outside Diameter | \( in \) | \( mm \) |
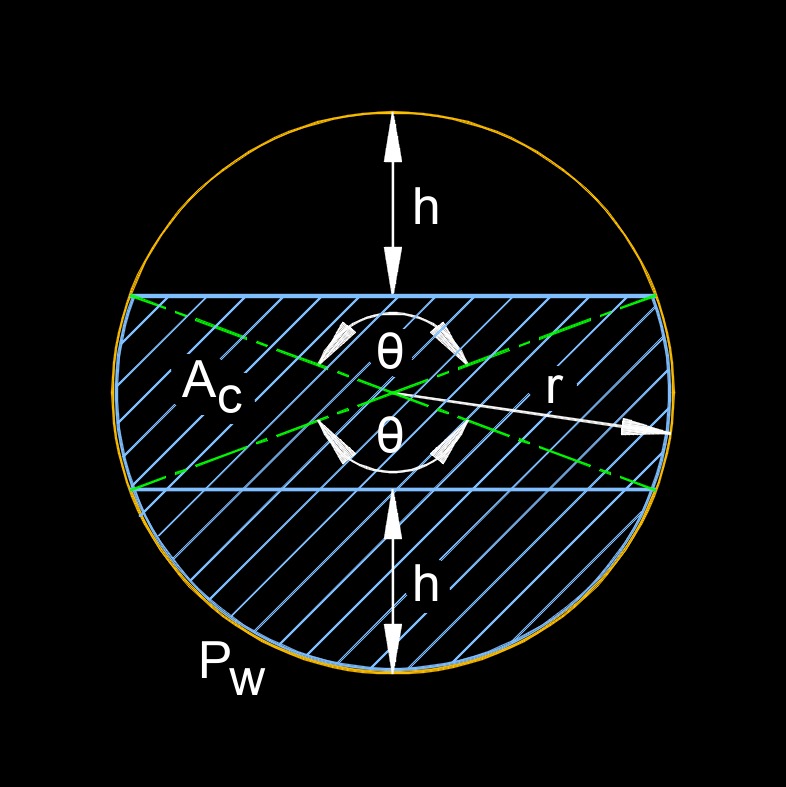Wetted perimeter is the portion of the pipe's interior circumference that is in direct contact with the flowing liquid. It's used in calculating hydraulic properties like hydraulic radius, which in turn influences flow velocity and resistance. For a circular pipe, the wetted perimeter depends on whether the pipe is flowing full or partially full. If the pipe is flowing completely full, the wetted perimeter is simply the entire circumference of the circle. However, if the pipe is only partially filled, the wetted perimeter is the length of the arc along the bottom and sides of the pipe that are submerged in the fluid. The wetted perimeter directly impacts the frictional losses experienced by the fluid as it moves through the pipe, a larger wetted perimeter generally means more contact area for friction, which can reduce flow velocity and overall flow rate for a given cross-sectional area.
