Temperature Change Formula |
||
|
\( \Delta T \;=\; T_f - T_i \) (Temperature Change) \( T_f \;=\; \Delta T + T_i \) \( T_i \;=\; T_f - \Delta T \) |
||
| Symbol | English | Metric |
| \( \Delta T \) = Temperature Change | \(^\circ F\) | \(^\circ C\) |
| \( T_f \) = Final Temperature | \(^\circ F\) | \(^\circ C\) |
| \( T_i \) = Initial Temperature | \(^\circ F\) | \(^\circ C\) |
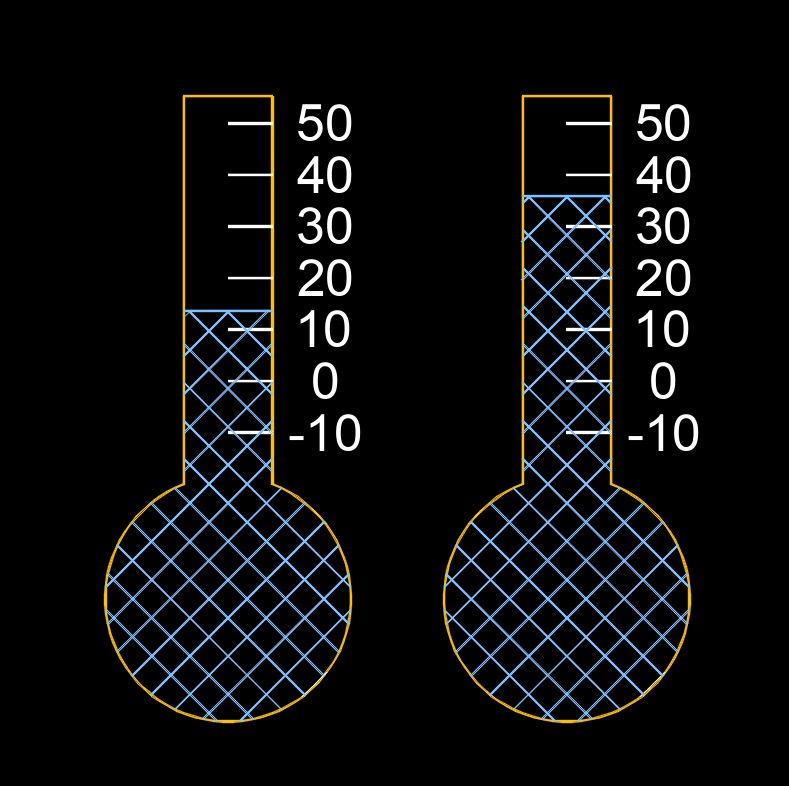
Temperature change, abbreviated as \(\Delta T\), is how much the temperature increases or decreases between two points in time or between two different locations. It represents the difference between a final temperature and an initial temperature, showing whether the system has warmed up, cooled down, or stayed nearly constant. Understanding the change in temperature is important in areas such as thermodynamics, heating and cooling processes, material expansion, and energy calculations, because temperature differences drive heat flow and affect how systems behave.
