Braking Distance on Grade
Braking Distance on Downgrade or Upgrade Formulas |
||
|
\( B_d \;=\; \dfrac{ V^2 }{ 30 \cdot \left( \dfrac{ a }{ 32.2 } \pm G \right) } \) \( B_d \;=\; \dfrac{ V^2 }{ 30 \cdot \left( \dfrac{ a }{ 32.2 } \pm \dfrac{ G }{ 100 } \right) } \) |
||
| Symbol | English | Metric |
| \( B_d \) = Braking Distance on Grade | \(ft\) | \(m\) |
| \( V \) = Design Speed | \(ft\;/\;sec\) | \(m\;/\;sec\) |
| \( a \) = Deceleration Rate | \(ft\;/\;sec\) | \(m\;/\;sec\) |
| \( G \) = Grade Percent Divided by 100 | \(dimensionless\) | \(dimensionless\) |
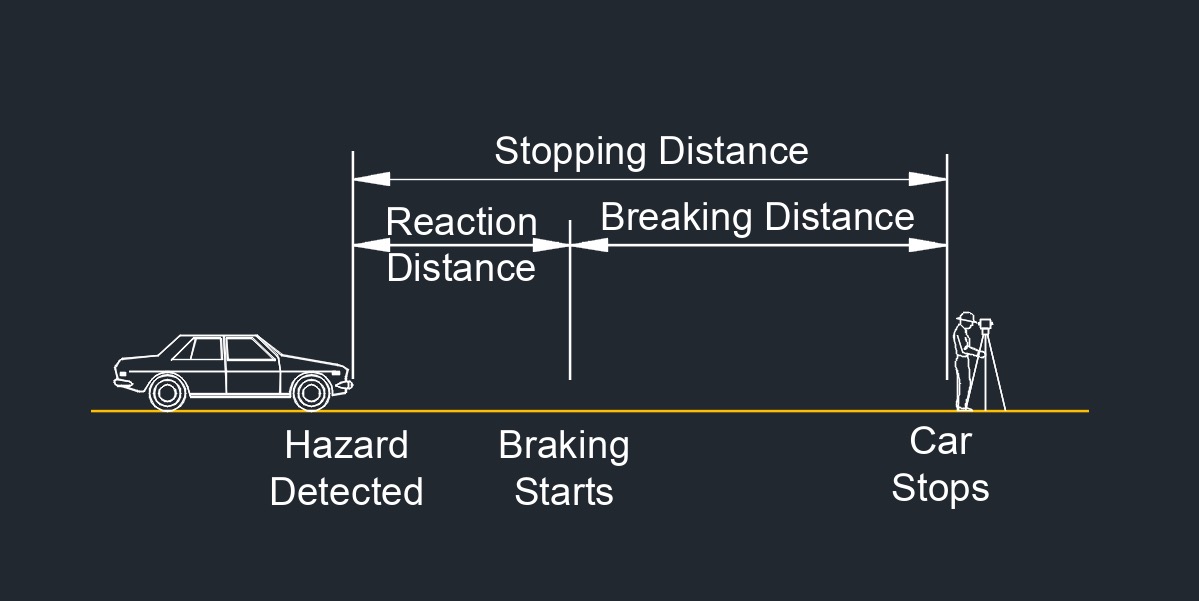
Braking distance on grade, abbreviated as \(B_d\), also called downhill or uphill slope, is the distance a vehicle travels from the moment the brakes are fully applied until the vehicle comes to a complete stop while driving on an incline. The presence of a grade adds complexity to the braking process, as the gravitational force due to the slope can influence the vehicle's acceleration or deceleration. When a vehicle is traveling on a downhill grade, the force of gravity aids in accelerating the vehicle, making it more challenging to slow down or stop. On the other hand, when a vehicle is driving uphill, the force of gravity acts against the vehicle's motion, potentially aiding in deceleration.
AASHTO Exhibit 3-2 Stopping Sight Distance on Grade |
||||||
| Design Speed | Stopping Sight Distance | |||||
| Downgrade | Upgrade | |||||
| 3% | 6% | 9% | 3% | 6% | 9% | |
| 15 | 80 | 82 | 85 | 75 | 74 | 73 |
| 20 | 116 | 120 | 126 | 109 | 107 | 104 |
| 25 | 158 | 165 | 173 | 147 | 143 | 140 |
| 30 | 205 | 215 | 227 | 200 | 184 | 179 |
| 35 | 257 | 271 | 287 | 237 | 229 | 222 |
| 40 | 315 | 333 | 354 | 289 | 278 | 269 |
| 45 | 378 | 400 | 427 | 344 | 331 | 320 |
| 50 | 446 | 474 | 507 | 405 | 388 | 375 |
| 55 | 520 | 553 | 593 | 469 | 450 | 433 |
| 60 | 598 | 638 | 686 | 538 | 515 | 495 |
| 65 | 682 | 728 | 785 | 612 | 584 | 561 |
| 70 | 771 | 825 | 891 | 690 | 658 | 631 |
| 75 | 866 | 927 | 1003 | 772 | 736 | 704 |
| 80 | 965 | 1035 | 1121 | 859 | 817 | 782 |
Calculating braking distance on a grade involves taking into account the effects of gravity, vehicle speed, braking efficiency, and other factors that contribute to stopping. The formula to calculate braking distance on a grade is more complex than the formula for flat terrain and includes additional components related to the grade angle and the influence of gravity. For example, when calculating braking distance on a downhill grade, the gravitational component that contributes to acceleration needs to be subtracted from the overall deceleration due to braking. Conversely, when calculating braking distance on an uphill grade, the gravitational component that opposes the vehicle's motion can potentially aid in deceleration.
Due to the complexities introduced by the grade, engineers and researchers use advanced mathematical models and simulation tools to accurately calculate braking distance on different types of grades. The actual calculation can depend on variables such as the grade angle, vehicle weight, tire grip, road conditions, and braking system efficiency.
In real-world scenarios, drivers should exercise caution when driving on grades, especially when going downhill. It's important to maintain a safe speed and use the brakes judiciously to prevent overheating and loss of braking effectiveness. On uphill grades, vehicles may naturally slow down due to the opposing gravitational force, but drivers should still be aware of their surroundings and maintain control of the vehicle.

