- See Article - Geometric Properties of Structural Shapes
area of a Tapered I Beam formula |
||
| \( A \;=\; l \cdot t + 2\cdot a \cdot \left( s + n \right) \) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( n \) = thickness | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( a \) = width | \( in \) | \( mm \) |
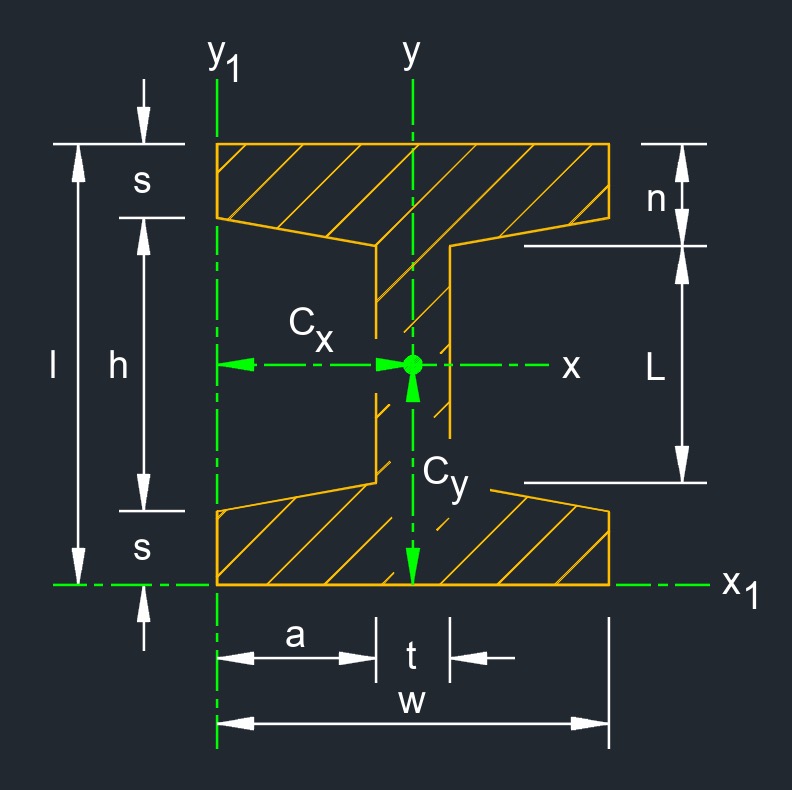A tapered I-beam, also called tapered beam or a tapered I-section, is a type of structural steel member that has a non-uniform cross-sectional shape along its length. Unlike a regular I-beam, which has a constant cross-sectional shape throughout its entire length, a tapered I-beam gradually changes its dimensions, usually becoming narrower or shallower as it extends along its length. This tapering can be gradual or more pronounced, depending on the specific engineering requirements of the structure. Tapered I-beams are often used in situations where the load distribution and structural requirements vary along the length of the beam.
Distance from Centroid of a Tapered I Beam formulas |
||
|
\( C_x \;=\; \dfrac{ w }{ 2 } \) \( C_y \;=\; \dfrac{ l }{ 2 } \) |
||
| Symbol | English | Metric |
| \( C \) = distance from centroid | \( in^2 \) | \( mm^2 \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Elastic Section Modulus of a Tapered I Beam formulas |
||
|
\( C_x \;=\; \dfrac{ w }{ 2 } \) \( C_y \;=\; \dfrac{ l }{ 2 } \) |
||
| Symbol | English | Metric |
| \( S \) = elastic section modulus | \( in^3 \) | \( mm^3 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Perimeter of a Tapered I Beam formula |
||
| \( P \;=\; 2\cdot w + 4\cdot s + 2\cdot L + 4 \cdot \sqrt{ \left( \dfrac{w - a}{2} \right)^2 + \left( s + n \right)^2 } \) | ||
| Symbol | English | Metric |
| \( P \) = perimeter | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( n \) = thickness | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( a \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Polar Moment of Inertia of a Tapered I Beam formulas |
||
|
\( J_z \;=\; I_x + I_y \) \( J_{z1} \;=\; I_{x1} + I_{y1} \) |
||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Radius of Gyration of a Tapered I Beam formulas |
||
|
\( k_x \;=\; \sqrt{ \dfrac{ \dfrac{1}{12} \cdot \left[ w\cdot l^3 - \dfrac{1}{4\cdot g} \cdot \left( h^4 - L^4 \right) \right] }{ l \cdot t + 2\cdot a \cdot \left( s + n \right) } } \) \( k_y \;=\; \sqrt{ \dfrac{ \dfrac{1}{3} \cdot \left[ w^3 \cdot \left( l - h \right) + L\cdot t^3 + \dfrac{g}{4} \cdot \left( w^4 - t^4 \right) \right] }{ l \cdot t + 2\cdot a \cdot \left( s + n \right) } } \) \( k_z \;=\; \sqrt{ k_{x}{^2} + k_{y}{^2} } \) \( k_{x1} \;=\; \sqrt{ \dfrac{ I_{x1} }{ A } } \) \( k_{y1} \;=\; \sqrt{ \dfrac{ I_{y1} }{ A } } \) \( k_{z1} \;=\; \sqrt{ k_{x1}{^2} + k_{y1}{^2} } \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
| \( n \) = thickness | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( a \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Second Moment of Area of a Tapered I Beam formulas |
||
|
\( I_x \;=\; \dfrac{1}{12} \cdot \left[ w\cdot l^3 - \dfrac{1}{4\cdot g} \cdot \left( h^4 - L^4 \right) \right] \) \( I_y \;=\; \dfrac{1}{3} \cdot \left[ w^3 \cdot \left( l - h \right) + L\cdot t^3 + \dfrac{g}{4} \cdot \left( w^4 - t^4 \right) \right] \) \( I_{x1} \;=\; l_{x} + A\cdot C_{y}{^2} \) \( I_{y1} \;=\; l_{y} + A\cdot C_{x}{^2} \) |
||
| Symbol | English | Metric |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( g \) = slope of taper | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Slope of Flange of a Tapered I Beam formula |
||
| \( g \;=\; \dfrac{ h - L }{ w - t } \) | ||
| Symbol | English | Metric |
| \( g \) = slope of taper | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |