Orifice center of head formula |
||
|
\( h_c \;=\; \dfrac{ \left( \dfrac{ Q }{ C_d \cdot A_o} \right)^2 }{ 2 \cdot G }\) (Orifice Center of Head) \( Q \;=\; A_o \cdot C_d \cdot \sqrt{ 2 \cdot G \cdot h_c } \) \( A_0 \;=\; \dfrac{ Q }{ C_d \cdot \sqrt{ 2 \cdot G \cdot h_c } }\) \( C_d \;=\; \dfrac{ Q }{ A_o \cdot \sqrt{ 2 \cdot G \cdot h_c } }\) \( h_c \;=\; \dfrac{ \left( \dfrac{ Q }{ C_d \cdot A_o} \right)^2 }{ 2 \cdot h_c }\) |
||
| Symbol | English | Metric |
| \( h_c \) = Orifice Center of Head | \( in \) | \( mm \) |
| \( Q \) = Orifice Flow Rate | \(ft^3 \;/\; sec\) | \(m^3 \;/\; s\) |
| \( A_o \) = Orifice Area | \(in^2 \) | \( mm^2 \) |
| \( C_d \) = Orifice Discharge Coefficient | \( dimensionless \) | \( dimensionless \) |
| \( G \) = Orifice Gravitational Constant | \(lbf-ft^2 \;/\; lbm^2\) | \(N - m^2 \;/\; kg^2\) |
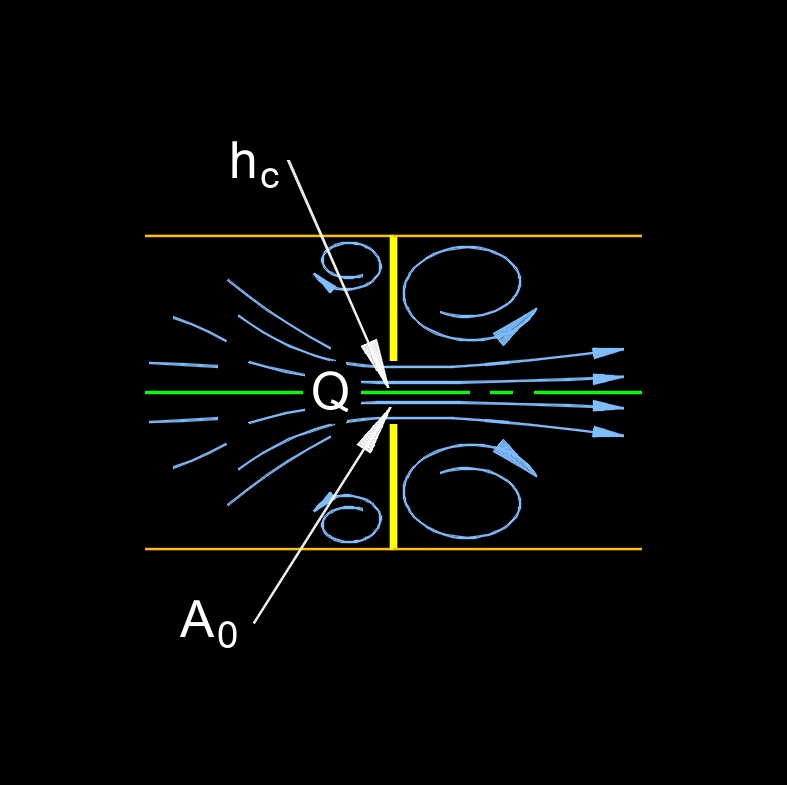Orifice center of head is when a fluid flows through an orifice plate, the constriction caused by the orifice leads to a pressure drop across the plate. The magnitude of this pressure drop is related to the flow rate. For accurate flow measurement, the location and geometry of the pressure taps used to measure this differential pressure relative to the orifice are crucial. Standards and best practices in flow measurement often refer to the "center" of the orifice as a reference point for specifying the placement of these pressure taps.
When analyzing flow through an orifice under a certain head, the height of the liquid level above the center of the orifice is a key parameter in determining the theoretical velocity and discharge rate according to Torricelli's law and its derivations. Therefore, the orifice center of head can be thought of as the reference elevation for measuring the effective pressure head driving the flow through the opening.
