Orifice Discharge Coefficient

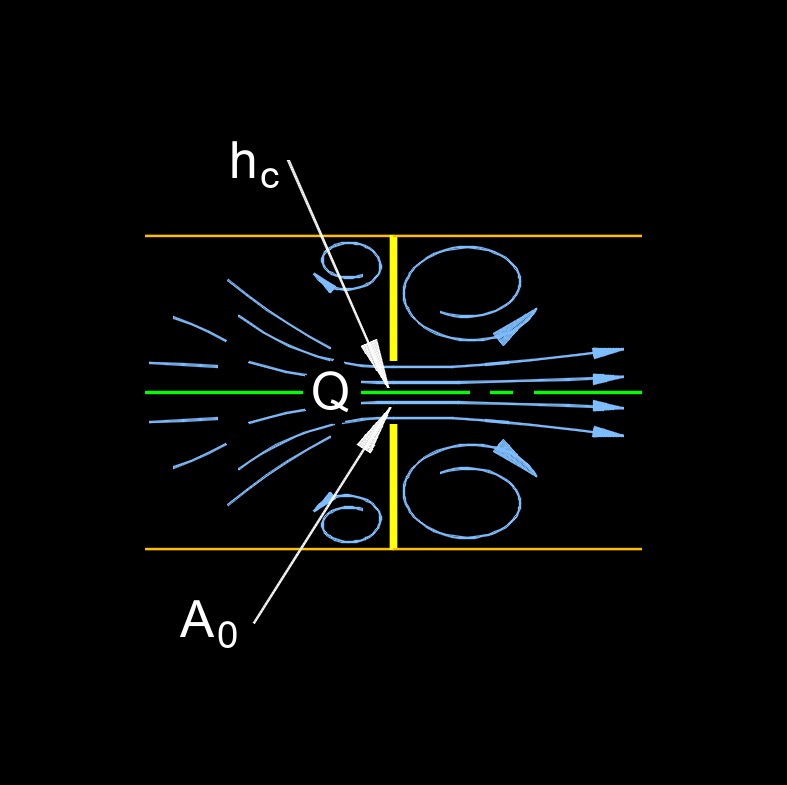Orifice discharge coefficient, abbreviated as \(C_d\), a dimensionless number, is used in fluid dynamics to describe the flow of a fluid (liquid or gas) through an orifice, which is a small opening or hole in a pipe or plate.  This coefficient represents the efficiency of the orifice in allowing the fluid to pass through it.

The orifice discharge coefficient takes into account various factors that affect the flow rate through the orifice, including the size and shape of the orifice, the fluid properties (density and viscosity), and the velocity of the fluid approaching the orifice.  It is typically determined experimentally through calibration tests and is specific to a particular orifice design and fluid flow conditions.

The orifice discharge coefficient is an essential parameter in industries such as fluid mechanics, engineering, and process control, where precise control of fluid flow is necessary.  Engineers and scientists use it to accurately predict and control flow rates through orifices in various applications, including pipelines, nozzles, and control valves.  Different orifice designs and flow conditions may have different discharge coefficients, so it's crucial to use the appropriate coefficient for a given situation to make accurate flow rate calculations or control adjustments.

 

Orifice Discharge Coefficient formula
\( C_d \;=\;   Q \;/\; A_o \; \sqrt { 2 \; G \; h_c }   \)     (Orifice Discharge Coefficient) \( Q \;=\; C_d  \; A_o  \; \sqrt{ 2 \; G \; h_c }    \)  \( A_0 \;=\; Q  \;/\; C_d \; \sqrt{ 2 \; G \; h_c }  \)  \( G \;=\; ( Q \;/\; C_d \; A_o  )^2  \;/\; 2  \; h_c  \)  \( h_c \;=\; ( Q \;/\; A_o \; C_d )^2  \;/\; 2  \; G  \)
Symbol	English	Metric
\( C_d  \) = Orifice Discharge Coefficient	\( dimensionless \)	\( dimensionless \)
\( Q \) = Orifice Flow Rate	\(ft^3 \;/\; sec\)	\(m^3 \;/\; s\)
\( A_o \) = Orifice Area	\( in^2 \)	\( mm^2 \)
\( G \) = Orifice Gravitational Constant	\(lbf-ft^2 \;/\; lbm^2\)	\(N - m^2 \;/\; kg^2\)
\( h_c \) = Orifice Center of Head	\( in \)	\( mm \)