Flow Rate Formula |
||
|
\( Q \;=\; A_c \cdot v \) (Flow Rate) \( A_c \;=\; \dfrac{ Q }{ v }\) \( v \;=\; \dfrac{ Q }{ A_c }\) |
||
| Symbol | English | Metric |
| \( Q \) = Flow Rate | \(ft^3 \;/\; sec\) | \(m^3 \;/\; s\) |
| \( A_c \) = Fluid Area Cross-section | \(in^2\) | \(mm^2\) |
| \( v \) = Fluid Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
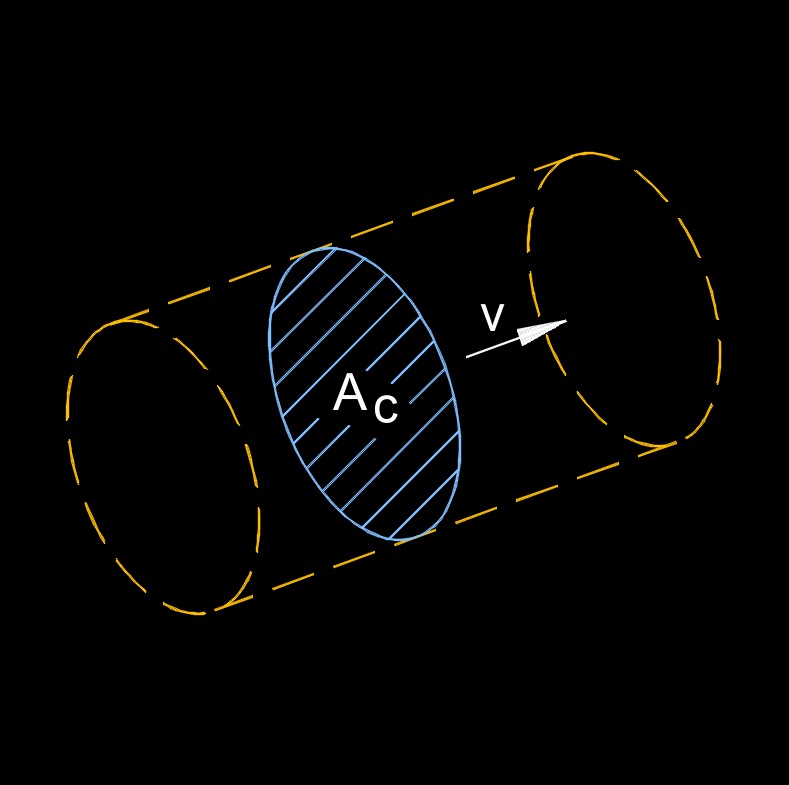Flow rate, abbreviated as Q, is the amount of fluid or gas that flows through a given point in a system per unit of time. The flow rate of a fluid or gas can be affected by a variety of factors, including the pressure differential, the viscosity and density of the fluid, and the size and shape of the pipe or duct through which it is flowing. Flow rate is an important consideration in many industrial and engineering applications, including fluid and gas systems, chemical processing, and HVAC systems.
In order to accurately measure flow rate, various types of flow meters are used, including volumetric flow meters, velocity flow meters, and mass flow meters. These devices typically use principles such as pressure, flow resistance, or thermal properties to determine the flow rate of the fluid or gas.
Flow rate can also be controlled using various devices, such as valves and regulators, which can be used to adjust the pressure differential or restrict the flow of the fluid or gas. This can be important in applications where precise control over the flow rate is required, such as in chemical processing or HVAC systems.
