Spring Rate Formula |
||
| \( n_s \;=\; \dfrac{ P }{ d_s }\) | ||
| Symbol | English | Metric |
| \( n_s \) = Spring Rate | \(lbf\;/\;in\) | \(kg\;/\;mm\) |
| \( P \) = Load | \( lbf \) | \( kg \) |
| \( d_s \) = Spring Displacement | \( in \) | \(mm \) |
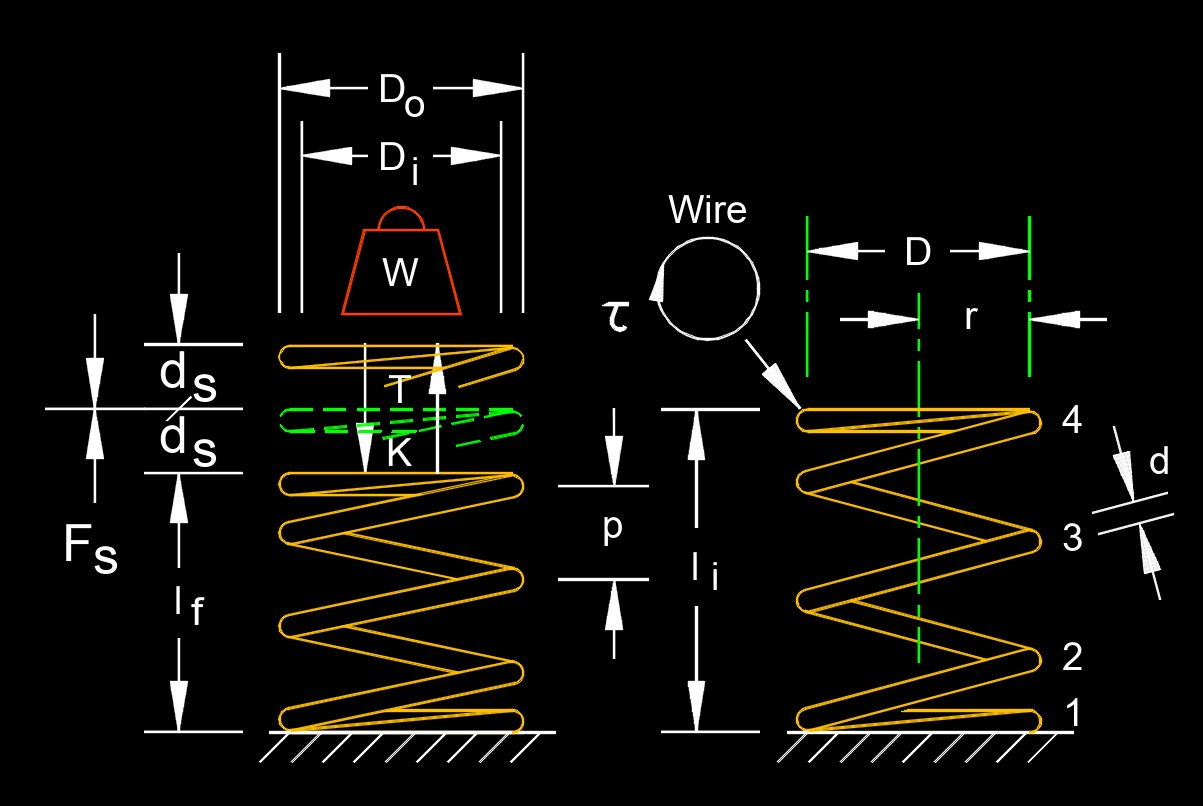Spring rate, abbreviated as \(n_s\), is not the same as spring load. The spring rate is based on the spring's working load. Spring rate is the rate of force or weight required to travel one unit of measurement. The lower the spring rate, the softer the spring. The softer the spring, the smother the ride. Spring load is the amount of weight a spring is designed to carry when compressed to a certain height.
Spring Rate Formula |
||
| \( n_s \;=\; \dfrac{ P - T_i }{ d_s }\) | ||
| Symbol | English | Metric |
| \( n_s \) = Spring Rate | \(lbf\;/\;in\) | \(kg\;/\;mm\) |
| \( P \) = Load | \( lbf \) | \( kg \) |
| \( T_i \) = Initial Tension | \( lbf \) | \( N \) |
| \( d_s \) = Spring Displacement | \( in \) | \(mm \) |
Spring Rate Formula |
||
| \( n_s \;=\; \dfrac{ G \cdot d^4 }{ 10.8 \cdot D \;cdotn_a }\) (rate per 360 degrees) | ||
| Symbol | English | Metric |
| \( n_s \) = Spring Rate | \(lbf\;/\;in\) | \(kg\;/\;mm\) |
| \( G \) = Shear Modulus of Material | \(lbf\;/\;in^2\) | \( Pa \) |
| \( d \) = Wire Diameter | \( in \) | \( mm \) |
| \( D \) = Mean Coil Diameter | \( in \) | \( mm \) |
| \( n_a \) = Number of Active Coils | \(dimensionless\) | \(dimensionless\) |
Spring Rate Formula |
||
| \( n_s \;=\; \dfrac{ G \cdot d^4 }{ 8 \cdot D^3 \cdot n_a }\) (pitch angle is less than 15 degrees or displacement per turn is less than D/4) | ||
| Symbol | English | Metric |
| \( n_s \) = Spring Rate | \(lbf\;/\;in\) | \(kg\;/\;mm\) |
| \( G \) = Shear Modulus of Material | \(lbf\;/\;in^2\) | \( Pa \) |
| \( d \) = Wire Diameter | \( in \) | \( mm \) |
| \( D \) = Mean Coil Diameter | \( in \) | \( mm \) |
| \( n_a \) = Number of Active Coils | \(dimensionless\) | \(dimensionless\) |