Spring Displacement
Spring Displacement formula |
||
|
\( d_s \;=\; \sqrt{ \dfrac{ 2 \cdot E_s }{ k_s } } \) (Spring Displacement) \( E_s \;=\; \dfrac{ d_s^2 \cdot k_s }{ 2 }\) \( k_s \;=\; \dfrac{ 2 \cdot E_s }{ d_s^2 }\) |
||
| Symbol | English | Metric |
| \( d_s \) = Spring Displacement | \( in \) | \( mm \) |
| \( k_s \) = Spring Constant | \( lbf \) | \( N \) |
| \( E_s \) = Spring Energy | \( lbf-ft \) | \( J \) |
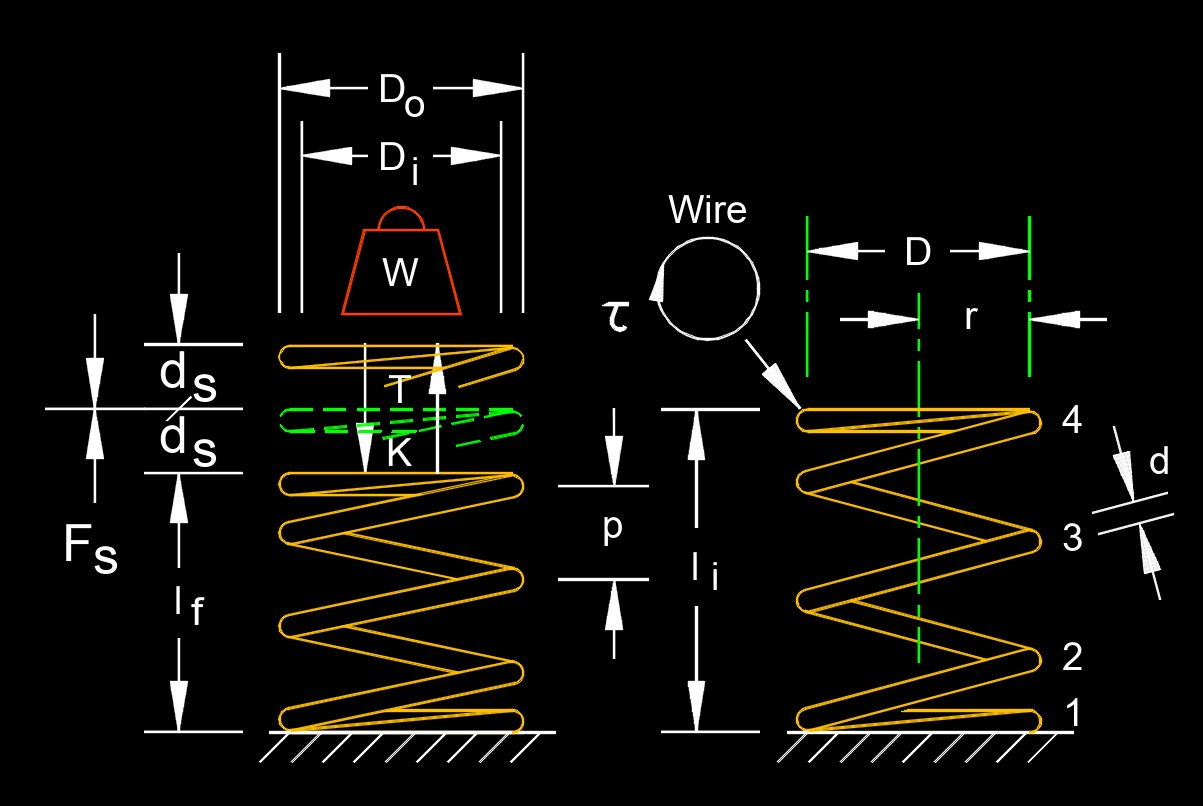
Spring displacement, abbreviated as \(d_s\), also called spring deformed, spring deflection or travel distance, is the distance or extent to which a spring has been compressed or stretched from its equilibrium or rest position. Springs are mechanical components that can store potential energy when deformed from their natural or resting state. This deformation can occur when an external force is applied to the spring, causing it to compress or extend depending on the type of spring. This concept is central to understanding how springs work in the context of Hooke's Law, which states that the force exerted by a spring is directly proportional to its displacement, as long as the limit of elasticity is not exceeded.
Spring Displacement formula |
||
|
\( d_s \;=\; \dfrac{ F_s }{ k_s }\) (Spring Displacement) \( F_s \;=\; d_s \cdot k_s \) \( k_s \;=\; \dfrac{ F_s }{ d_s }\) |
||
| Symbol | English | Metric |
| \( d_s \) = Spring Displacement | \( in \) | \( mm \) |
| \( k_s \) = Spring Constant | \( lbf \) | \( N \) |
| \( F_s \) = Spring Force (Hooke's Law) | \( lbf \) | \( N \) |
The amount of displacement a spring undergoes is often a critical parameter in various mechanical systems and engineering applications. It can affect how a system functions, such as in suspension systems for vehicles, where the spring displacement determines the vehicle's ride height and comfort.

