Equilibrium

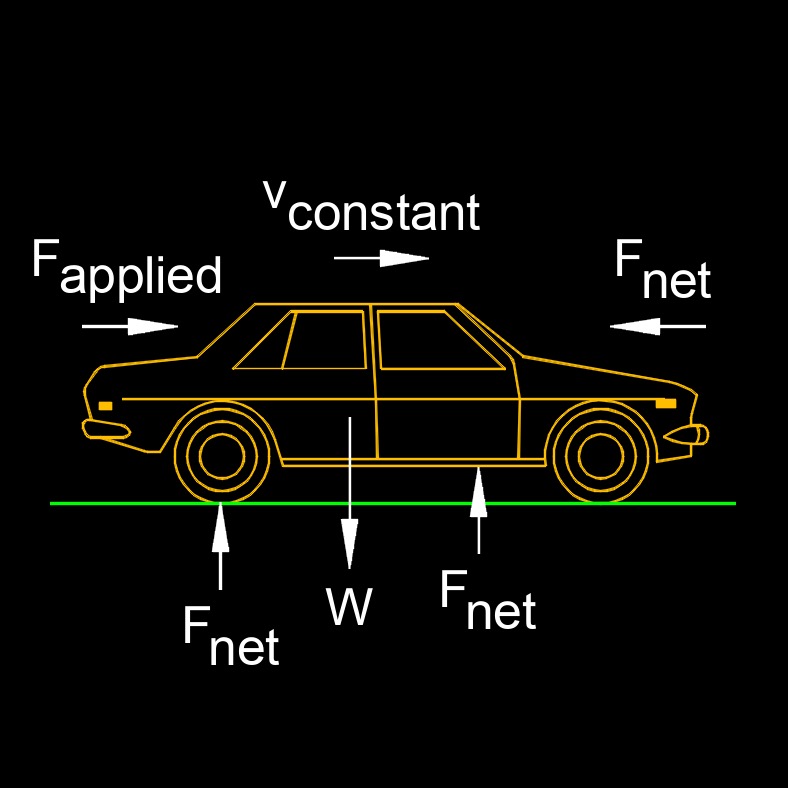Equilibrium is when all the net external forces that act upon an object are balanced.  This does not mean all the forces are equal to each other.  If the net force is zero, then the net external forces in any direction is zero.  Any object that is at rest is in equilibrium.  \(\large{  F_{net} = 0  }\)

Equilibrium Types

Static Equilibrium  -  Static equilibrium occurs when an object is at rest and remains at rest.  In static equilibrium, the net force acting on the object is zero, and the net torque is also zero if the object can rotate.  This means that all the forces and torques acting on the object balance each other out, resulting in no acceleration.  The object remains stationary.
Translational Equilibrium  -  In translational equilibrium, the sum of all the forces acting on the object in various directions is zero.  Mathematically, it can be represented as ΣF = 0, where ΣF is the vector sum of all the forces.
Rotational Equilibrium  -  In rotational equilibrium, the sum of all the torque acting on the object is zero.  Mathematically, it can be represented as Στ = 0, where Στ is the vector sum of all the torques.
Dynamic Equilibrium  -  Dynamic equilibrium occurs when an object is in motion at a constant velocity, and there is no net acceleration.  In this case, the sum of all the forces acting on the object is still zero, but the object is not at rest, it moves with a constant speed in a straight line.  Dynamic equilibrium can also apply to rotational motion, where the object rotates at a constant angular velocity.
Translational Dynamic Equilibrium  -  In this case, ΣF = 0, and the object moves with a constant velocity.
Rotational Dynamic Equilibrium  -  In this case, Στ = 0, and the object undergoes constant angular velocity without any change in its rotational motion.

Understanding and applying the principles of equilibrium are fundamental in various branches of physics, such as mechanics, statics, and dynamics.  Engineers and physicists use these concepts to analyze and design structures, machines, and systems that are stable and operate as intended, whether at rest or in motion.

 

Distance from Equilibrium formula
\( x \;=\; x_0  - ( F \;/\; k_s ) \)     (Distance ftom Equilibrium) \( x_0 \;=\; x  + ( F \;/\; k_s )\) \( F \;=\; x_0 \; k_s - x \; k_s   \) \( k_s \;=\;   F \;/\; x_0 - x \)
Synbol	English	Metric
\( x \) = Distance from Equilibrium	\(in\)	\(mm\)
\( x_0 \) = Spring Equilibrium Position	\(in\)	\(mm\)
\( F \) = Force	\(lbf\)	\(N\)
\( k_s \) = Spring Force Constant	\(lbf-ft\)	\(N\;/\;m\)

 

Spring Equilibrium Position formula
\( x_0 \;=\; ( F \;/\; k_s )  + x \)     (Spring Equilibrium Position) \( F \;=\; k_s \; ( x_0 - x ) \) \( k_s \;=\;   F \;/\; x_0 - x \) \( x \;=\; x_0 - ( F \;/\; k_s ) \)
Symbol	English	Metric
\( x_0 \) = Spring Equilibrium Position	\(in\)	\(mm\)
\( F \) = Force	\(lbf\)	\(N\)
\( k_s \) = Spring Force Constant	\(lbf-ft\)	\(N\;/\;m\)
\( x \) = Distance from Equilibrium	\(in\)	\(mm\)