Vector

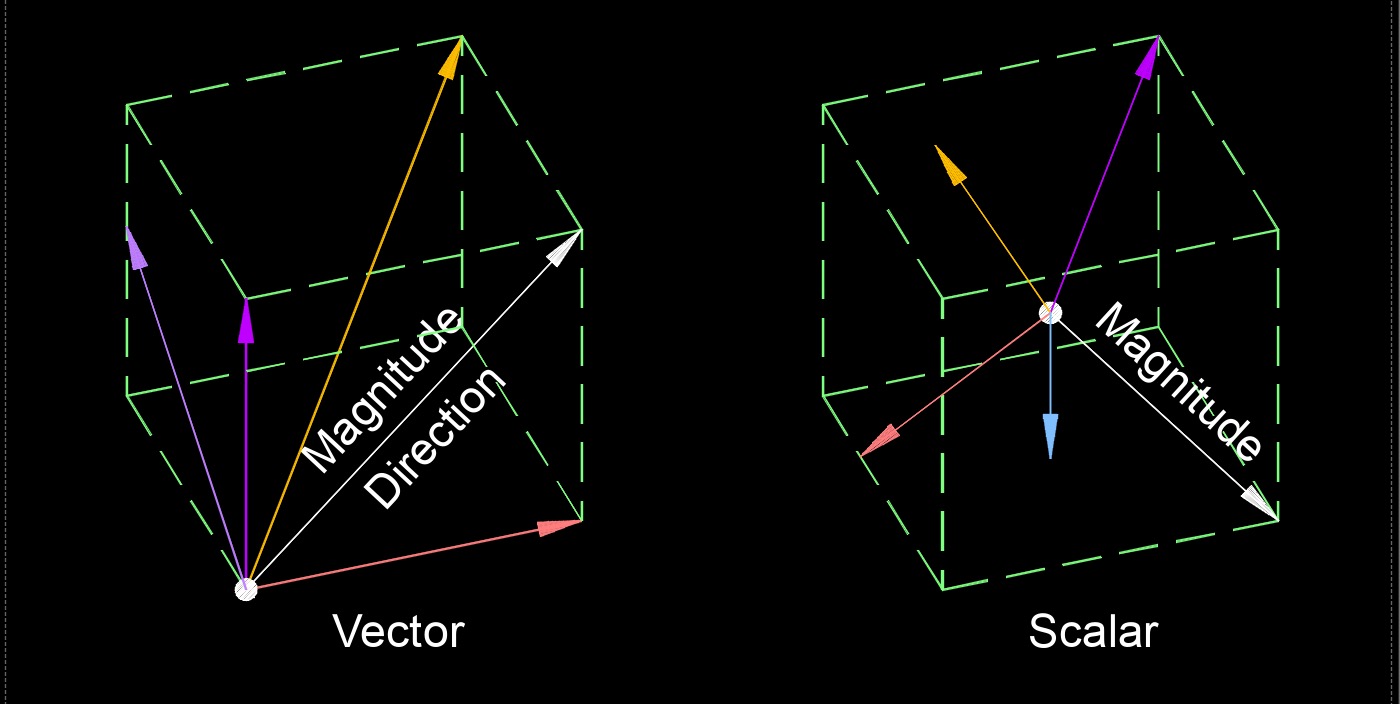In physics and mathematics, a vector is a mathematical entity that has both magnitude and direction.  It is used to represent quantities that have both a size or magnitude and a specific direction in space.

• See Articles  -  Scalar

A vector can be described using coordinates or components in a coordinate system, such as Cartesian coordinates (x, y, z) in three-dimensional space.  Each component of a vector represents the magnitude of the vector along a specific axis.  Vectors can undergo various operations, including addition, subtraction, and scalar multiplication.  When two vectors are added or subtracted, their magnitudes and directions are combined accordingly.  Scalar multiplication involves multiplying a vector by a scalar, which results in scaling the magnitude of the vector without changing its direction.

Here is a list of common vector quantities: acceleration, alternating current, angular acceleration, angular momentum, angular velocity, bouyancy force, centrifugal force, current density, displacement, distance, drag, electric field, force, friction, gravity, gravitational field, gravitational force, impulse, lift, magnetic field, magnetic flux, momentum, polarization, shear stress, temperature gradient, tension, thrust, torque, velocity, and weight.

Vectors are concepts in physics and mathematics.  Understanding vector quantities is essential for various fields of science, engineering, and mathematics, as they provide a concise and powerful way to describe physical phenomena and mathematical relationships involving direction and magnitude.

Definition  -  A vector quantity is a physical quantity that has both magnitude and direction.  Unlike scalar quantities, vectors are characterized by not only their size but also the specific direction in which they act.
Representation  -  Vectors are typically represented by arrows, where the length of the arrow corresponds to the magnitude of the vector, and the direction of the arrow represents the direction of the vector.  Alternatively, vectors can be represented algebraically using ordered lists of components or in terms of unit vectors along coordinate axes.
Components  -  Vectors can be broken down into components along different axes in a coordinate system.
Mathematical Operations  -  Vectors can undergo various mathematical operations, including addition, subtraction, scalar multiplication, dot product, cross product, and vector projection.  These operations are performed taking into account both the magnitudes and directions of the vectors involved.
Units  -  Vectors are associated with units of measurement that match the properties being measured.
Addition and Subtraction  -  When adding or subtracting vectors, both their magnitudes and directions must be considered.  Vectors are added or subtracted by combining or separating their components along each axis.
Scalar Multiplication  -  Vectors can be multiplied by scalar quantities, resulting in a vector with a magnitude that is scaled by the scalar and a direction that remains unchanged.
Physical Laws  -  Many fundamental physical laws involve vector quantities.
Geometric Interpretation  -  Vectors can be interpreted geometrically as directed line segments connecting two points in space.  This interpretation is particularly useful in visualizing vector addition, subtraction, and geometric transformations.

Similarities Between Scalar and Vector Quantities

Scalar and vector quantities both represent physical properties or measurements, but they differ in how they are described and what information they convey.  While scalar and vector quantities share these similarities, their differences are also significant, particularly in terms of the information they convey (direction for vectors) and how they are manipulated in mathematical and physical contexts.

Magnitude  -  Both scalar and vector quantities have a magnitude associated with them.  The magnitude represents the size or quantity of the property being measured.
Mathematical Operations  -  Both scalar and vector quantities can undergo mathematical operations such as addition, subtraction, multiplication, and division.  Scalars are added or subtracted directly, while vectors are added or subtracted based on both their magnitudes and directions.
Representation  -  Both scalar and vector quantities can be represented graphically.  Scalars are represented by a single number or point on a scale, while vectors are represented by arrows indicating both magnitude and direction.
Units  -  Both scalar and vector quantities are associated with units of measurement.  Scalars have units that match the property being measured, while vectors have units that match the combination of properties being measured.
Physical Meaning  -  Both scalar and vector quantities describe physical properties or measurements of objects or phenomena in the physical world.  Scalars describe quantities like distance, speed, temperature, energy, etc., while vectors describe quantities like displacement, velocity, force, acceleration, etc.
Mathematical Framework  -  Both scalar and vector quantities are integral parts of mathematical frameworks used to describe physical phenomena.  Scalars are represented as single values, while vectors are represented as arrays of values or as mathematical objects with magnitude and direction.