Torque
Torque Formula |
||
|
\( \tau \;=\; r \cdot F \cdot sin( \theta ) \) (Torque) \( r \;=\; \dfrac{ \tau }{ F \cdot sin ( \theta ) } \) \( F \;=\; \dfrac{ \tau }{ r \cdot sin ( \theta ) } \) \( \theta \;=\; \dfrac{ \tau }{ r \cdot F } \) |
||
| Symbol | English | Metric |
| \( \tau \) (Greek symbol tau) = Torque | \(lbf-ft\) | \(N-m\) |
| \( r \) = Radius is the Distance from the Pivot Point | \(in\) | \(mm\) |
| \( F \) = Magnitude of the Force Applied | \(lbf\) | \(N\) |
| \( \theta \) (Greek symbol theta) = Angle Between the Force Vector and the Leverage Arm Vector | \(deg\) | \(rad\) |
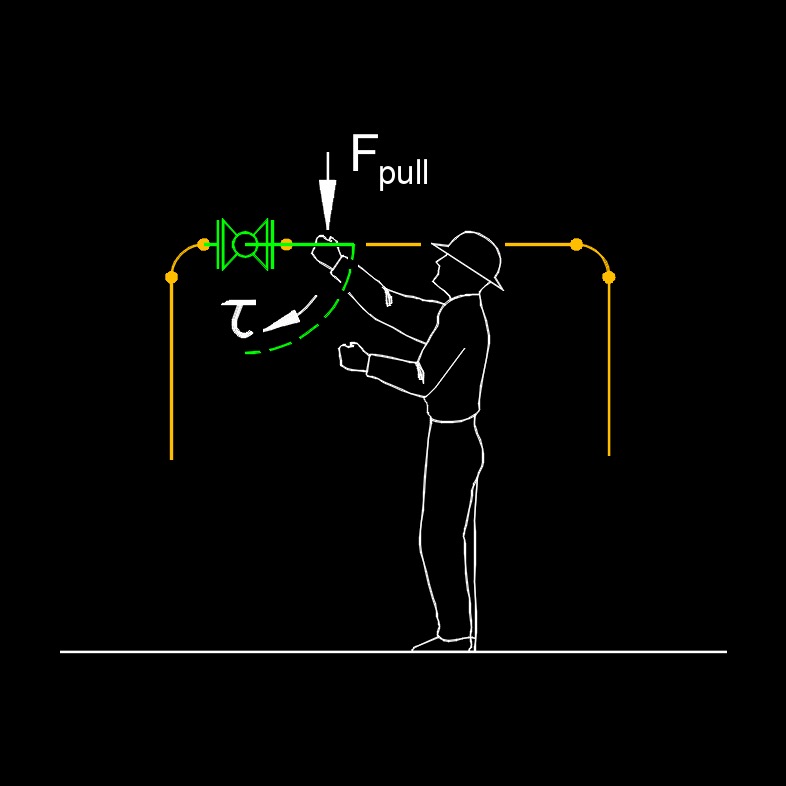 Torque, \( \tau \) (Greek symbol tau), also called moment of force, is a physical quantity that measures the rotational effect of a force applied to an object around a pivot point or axis. It is the rotational equivalent of linear force, causing an object to rotate or twist rather than move in a straight line. Torque depends on two key factors: the magnitude of the force applied and the distance from the axis of rotation to the point where the force is applied, known as the lever arm or moment arm. Torque plays a critical role in many applications, such as in engines, where it quantifies the turning power that drives machinery, or in everyday tasks like tightening a bolt with a wrench, where a longer wrench increases the lever arm, making it easier to apply torque. Essentially, torque determines how effectively a force can cause or change rotational motion, making it a fundamental concept in mechanics and engineering.
Torque, \( \tau \) (Greek symbol tau), also called moment of force, is a physical quantity that measures the rotational effect of a force applied to an object around a pivot point or axis. It is the rotational equivalent of linear force, causing an object to rotate or twist rather than move in a straight line. Torque depends on two key factors: the magnitude of the force applied and the distance from the axis of rotation to the point where the force is applied, known as the lever arm or moment arm. Torque plays a critical role in many applications, such as in engines, where it quantifies the turning power that drives machinery, or in everyday tasks like tightening a bolt with a wrench, where a longer wrench increases the lever arm, making it easier to apply torque. Essentially, torque determines how effectively a force can cause or change rotational motion, making it a fundamental concept in mechanics and engineering.

