Compression

Compression, abbreviated as K, is the force (pressure) acting on a material.  Compression is the process of reducing the volume or increasing the density of a substance, typically by applying external forces.  It involves the application of pressure to compress or squeeze a material, resulting in a decrease in its volume.

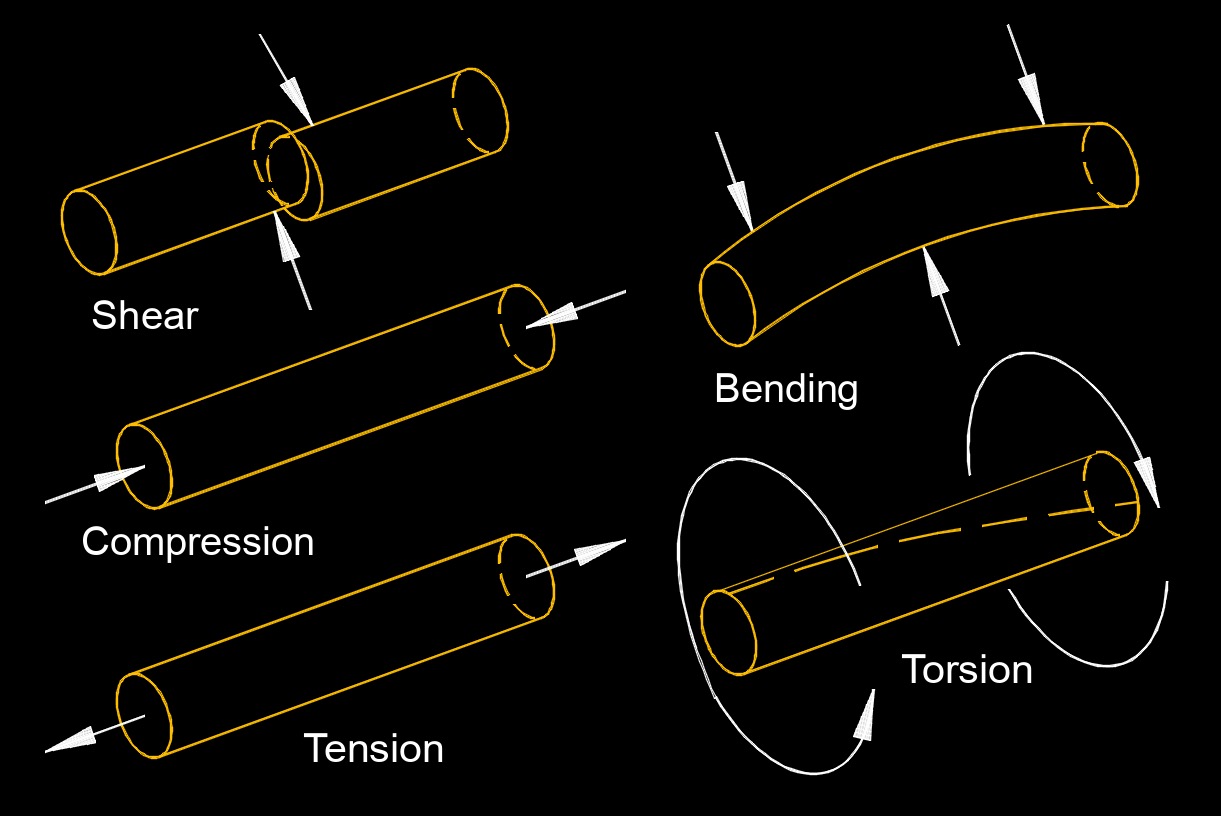Compression is used in physics and engineering.  It is used in various applications, including power generation, manufacturing, construction, transportation, and materials science.  Understanding the behavior of materials under compression is crucial for designing structures, machines, and systems that can withstand and utilize compressive forces effectively.

 

Compression formula
\( \Delta l \;=\;  l_f - l_i  \)
Symbol	English	Metric
\( \Delta l \) = Length Change	\( in \)	\( mm \)
\( l_f \) = Final Length	\( in \)	\( mm \)
\( l_i \) = Initial Length	\( in \)	\( mm \)

    

Compression formulas
\( \Delta d \;=\; \epsilon_{di} \; d_i  \)  \( \Delta d \;=\; ( \mu \; \sigma \;/\; \lambda ) \; d_i  \)  \( \Delta d \;=\; ( \mu \; p \;/\; \lambda \; A ) \; d_i  \)  \( \Delta l \;=\; l_f - l_i  \) \( \Delta l \;=\; \lambda \; l_i  \) \( \Delta l \;=\; ( \sigma \;/\; \lambda ) \; l_i  \) \( \Delta l \;=\; ( p \;/\; \lambda \; A ) \; l_i  \)
Symbol	English	Metric
\( \Delta d \) = Depth Change	\( in \)	\( mm \)
\( \Delta l \) = Length Change	\( in \)	\( mm \)
\( A \) = Area	\( in^2 \)	\( mm^2 \)
\( \lambda \)  (Greek symbol lambda) = Elastic Modulus	\(lbf\;/\;in^2\)	\(Pa\)
\( l_f \) = Final Length	\( in \)	\( mm \)
\( l_i \) = Initial Length	\( in \)	\( mm \)
\( \mu \)  (Greek symbol mu) = Poisson's Ratio	\( dimensionless \)	\( dimensionless \)
\( p \) = Pressure Under Consideration	\(lbf\;/\;in^2\)	\(Pa\)
\( \epsilon \)  (Greek symbol epsilon) = Strain	\(in\;/\;in\)	\(mm\;/\;mm\)