Elastic Modulus

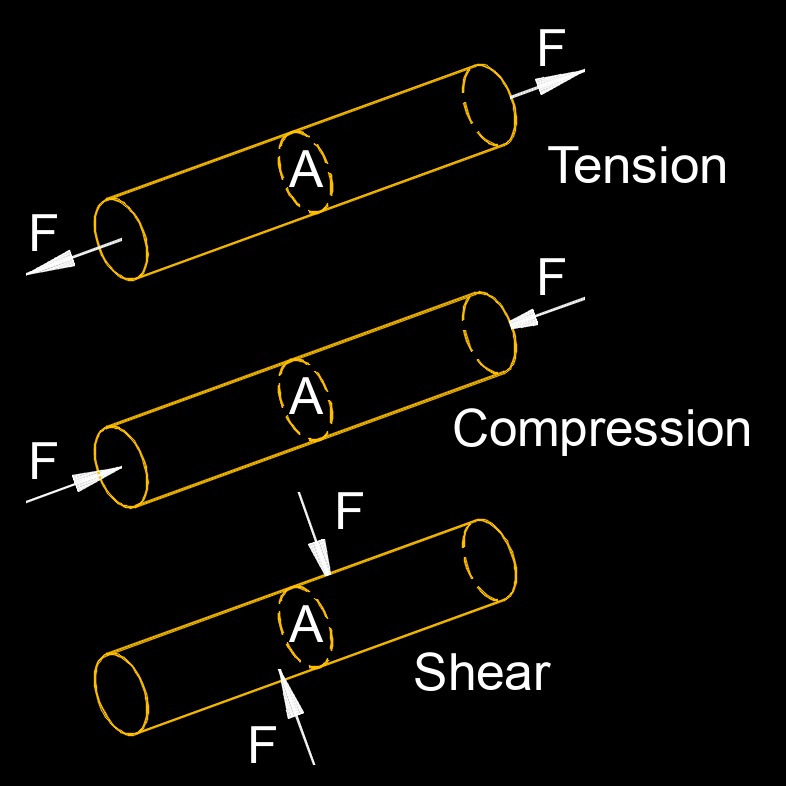
Elastic modulus (Young's modulus), abbreviated as \(\lambda\) (Greek symbol lambda), also called modulus of elasticity, is a measure of a material's stiffness or ability to resist deformation under an applied force.  The elastic modulus formula expresses the relationship between stress and strain in a material.  The higher the elastic modulus, the greater the material's ability to withstand deformation without breaking or yielding.

The elastic modulus is an important property of materials, and is used in the design and analysis of many structures, including buildings, bridges, and aircraft.  It is also used in the manufacture of various products, such as springs, cables, and metal beams, where a high level of stiffness is required.

 

Elastic Modulus formula
\( \lambda \;=\; \sigma \;/\; \epsilon \)     (Elastic Modulus) \( \sigma \;=\; \lambda  \;  \epsilon  \)  \( \epsilon \;=\; \sigma \;/\; \lambda \)
Symbol	English	Metric
\( \lambda \)  (Greek symbol lambda) = Elastic Modulus (psi)	\(lbf \;/\; in^2\)	\(Pa\)
\( \sigma \)  (Greek symbol sigma) = Stress Applied to the Material (psi)	\(lbf \;/\; in^2\)	\(Pa\)
\( \epsilon \)  (Greek symbol epsilon) = Strain of the Material	\(dimensionless\)	\(dimensionless\)