Stress

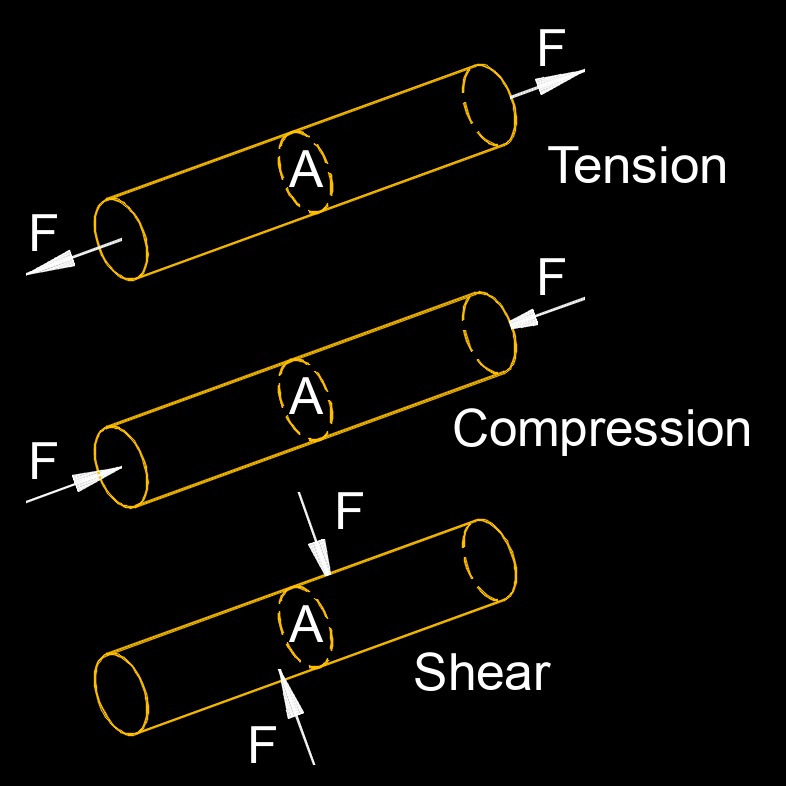
Stress, abbreviated as \(\sigma \) (Greek symbol sigma), also called normal stress, is the force per unit area cross-section.  The maximum stress of a material before it breaks is called breaking stress or ultimate tensial stress. 

In physics and engineering, stress refers to the internal force or pressure that acts on a material when it is subjected to external loads or forces.  It is a measure of the intensity of the internal forces within a material, which can cause deformation or changes in shape.

Stress is an essential concept in materials science, structural engineering, and mechanics.  Understanding the stress behavior of materials is crucial for designing structures, predicting failure points, ensuring safety, and selecting appropriate materials for specific applications.  Different materials have different stress limits, known as yield strength, ultimate strength, or breaking strength, beyond which they may experience permanent deformation or failure.

Stress Types

• Bulk Stress (Volume Stress)  -  The volume of the body changes due to the stress.
• Compressive Stress  -  The opposite of tensile stress.
• Cylinder Hoop Stress  -  The circumference stress in a cylinder of pipe having both ends closed due to internal pressure.
• Fatigue Stress  -  Failure or weakening of a material due to repetition and load cycling.
• Flow Stress  -  When a mass of flowing fluid indicates a dynamic pressure on a conduit wall.
• Hoop Stress  -  The circumferential and perpendicular stress to the axis imposed on a cylinder wall when exposed to an internal pressure load.
• Hydraulic Stress  -  The internal force per unit area when the force is applied by the fluid on the body.
• Longitudinal Stress  - When the length of the body changes its length by normal stress that is applied.
• Pressure Stress  -  Stresses induced in vessels containing pressurized materials.
• Radial Stress  -  The stress towards or away from the central axis of a curved member.
• Residual Stress  -  Stresses caused by manufacturing processes in a solid material after the origional cause has been removed.
• Shear Stress (Tangential Stress)  -  Tends to deform the material by breaking rather than stretching without changing the volume by restraining the object.
• Structural Stress  -  Stresses produced in structural members because of the weight they support.
• Tensile Stress  -  A stress in which the two sections of material on either side of a stress plane tend to pull apart or elongate.
• Thermal Stress  -  Whenever temperature gradients are present in a material.