Ultimate Tensile Strength Formula |
||
|
\( UTS \;=\; \dfrac{ F }{ A_c }\) (Ultimate Tensile Strength) \( F \;=\; UTS \cdot A_c \) \( A_c \;=\; \dfrac{ F }{ UTS }\) |
||
| Symbol | English | Metric |
| \( UTS \) = Ultimate Tensile Stress | \(lbf\;/\;in^2\) | \( Pa \) |
| \( F \) = Force or Maximum Load | \( lbf \) | \( N \) |
| \( A_c \) = Material Area Cross-section | \( in^2 \) | \( mm^2 \) |
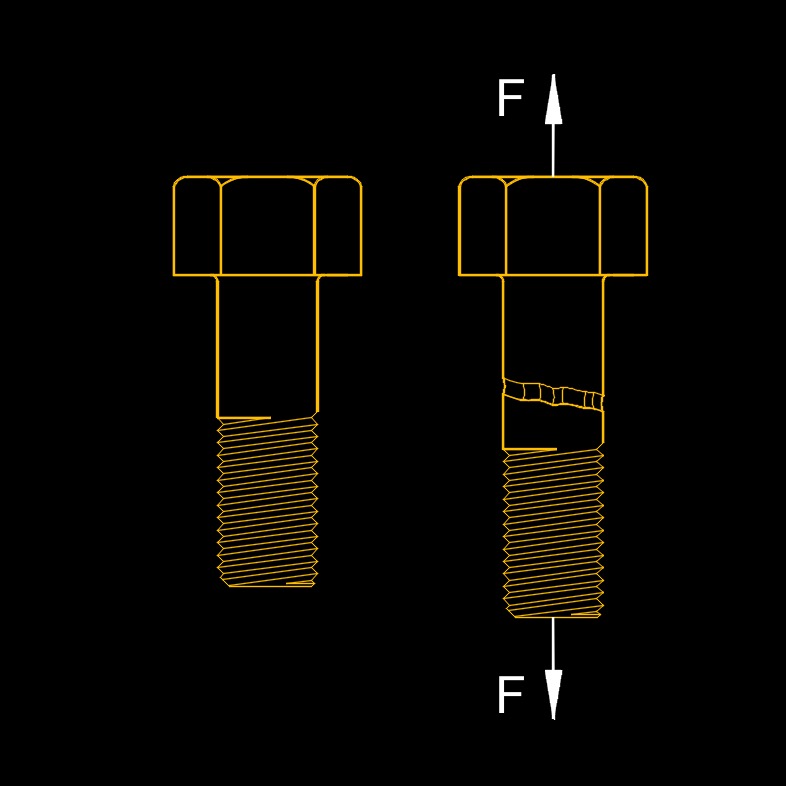Ultimate tensile strength, abbreviated as UTS, also called tensile strength or ultimate strength, is the maximum stress a material can resist before it starts to elongate. UTS is a mechanical property that represents the maximum stress a material can withstand before it fractures or breaks under tensile loading. It is a measure of the material's resistance to being pulled apart or stretched. When a material is subjected to a tensile force, it undergoes deformation until it reaches its ultimate tensile strength. At this point, the material experiences the maximum stress it can withstand before failure occurs. Failure may manifest as fracture, tearing, or separation of the material.
UTS is typically determined through a tensile test, where a sample of the material is subjected to axial tension until it ruptures. During the test, the load applied to the material and the corresponding elongation or deformation are measured. The ultimate tensile strength is then calculated by dividing the maximum load applied to the sample by its original area cross-section.
UTS is an important property in materials engineering and structural design as it provides insights into the strength and performance limits of a material. The UTS of a material is influenced by factors such as its composition, microstructure, processing conditions, and any defects or impurities present. Different materials exhibit varying ultimate tensile strengths, with some materials being inherently stronger than others.
