Thermal Stress

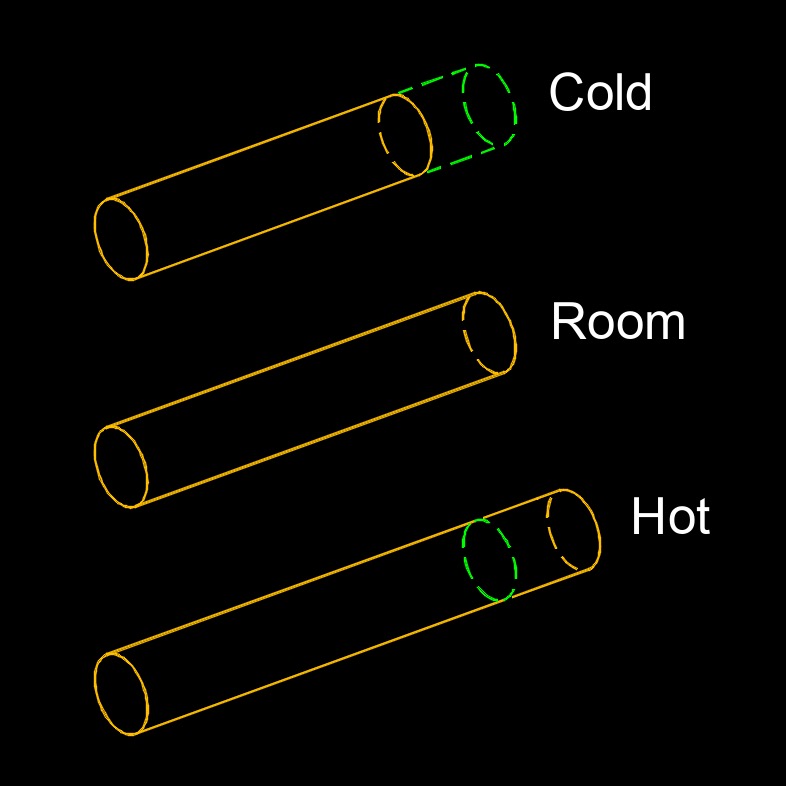Thermal stress, abbreviated as \( \sigma_t \) (Greek symbol sigma), is the change in the temperature of the material that causes expansion or contraction.  The change in length is porportional to the amount of heat applied.  When a material is subjected to non-uniform temperature distribution or rapid temperature changes, differential expansion or contraction can lead to internal forces and deformations, resulting in thermal stress.

Thermal stress comes from the mismatch in the thermal expansion coefficients between different materials or different regions within the same material.  Each material has a characteristic thermal expansion coefficients, which quantifies the change in dimension change in temperature.  When the temperature changes, materials expand or contract accordingly.  However, if materials with different thermal expansion coefficients are joined together, the differential expansion or contraction can cause stress and strain in the material.

For example, consider a metal pipe exposed to high temperature fluid.  The inner portion of the pipe heated by the fluid expands more than the outer portion that remains at a lower temperature.  This differential expansion creates internal stresses within the pipe, potentially leading to deformation or even structural failure.  Thermal stress can also occur within a homogeneous material if there is a non-uniform temperature distribution.  For instance, heating or cooling a metal bar on one side while the other side remains at a different temperature can create thermal stress due to the uneven expansion or contraction.

Managing and mitigating thermal stress is crucial in many engineering applications, such as in the design of structures, pipes, and electronic devices.  Techniques like thermal insulation, use of expansion joints, and appropriate material selection can help minimize the detrimental effects of thermal stress and ensure the structural integrity and performance of the system.

Thermal Stress Formula
\( \sigma_t \;=\; \alpha \; E \; \Delta T   \)     (Thermal Stress) \( \alpha \;=\;   \sigma_t \;/\; E \; \Delta T \)  \( E \;=\; \sigma_t \;/\; \alpha \; \Delta T \)  \( \Delta T \;=\;   \sigma_t \;/\; \alpha \; E \)
Symbol	English	Metric
\( \sigma_t \)  (Greek symbol sigma) = Thermal Stress	\(lbf \;/\; in^2\)	\(Pa\)
\( \alpha \)  (Greek symbol alpha) = Thermal Expansion Coefficient	\(in \;/\; in-F\)	\(mm \;/\; mm-C\)
\( E \) = Elastic Modulus	\(lbf \;/\; in^2\)	\(Pa\)
\( \Delta T \) = Change Temperature	\(F\)	\(C\)