Skip to main content

Right Hexagonal Prism

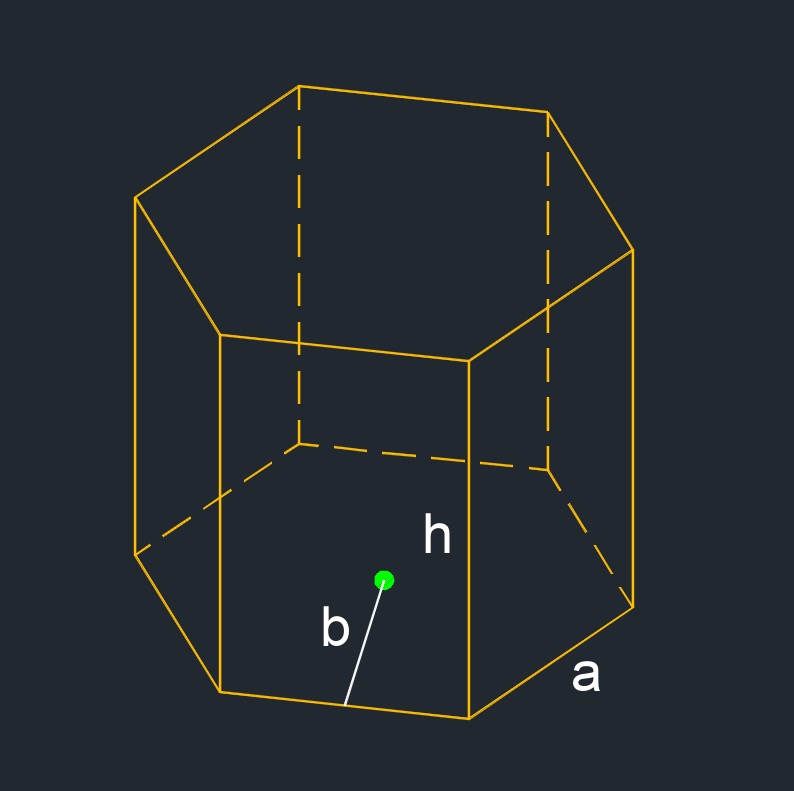
Right hexagon prism (a three-dimensional figure) is where each face is a regular polygon with equal sides and equal angles.
Long diagonal always crosses the center point of the hexagon.
Short diagonal does not cross the center point of the hexagon.
36 base diagonals
12 face diagonals
36 space diagonals
2 bases
18 edges
6 side faces
12 vertexs

Base Area of a Right Hexagonal Prism formula
$A_b \;=\; 3 \cdot \sqrt{3} \cdot \dfrac{ a^2 }{ 2 }$
Symbol	English	Metric
$A_b$ = base area	$in^2$	$mm^2$
$a$ = edge	$in$	$mm$

Base Long Diagonal of a Right Hexagon formula Long diagonal always crosses the center point of the hexagon.
$D_l \;=\; 2 \cdot a$
Symbol	English	Metric
$D_l$ = long diagonal	$in$	$mm$
$a$ = edge	$in$	$mm$

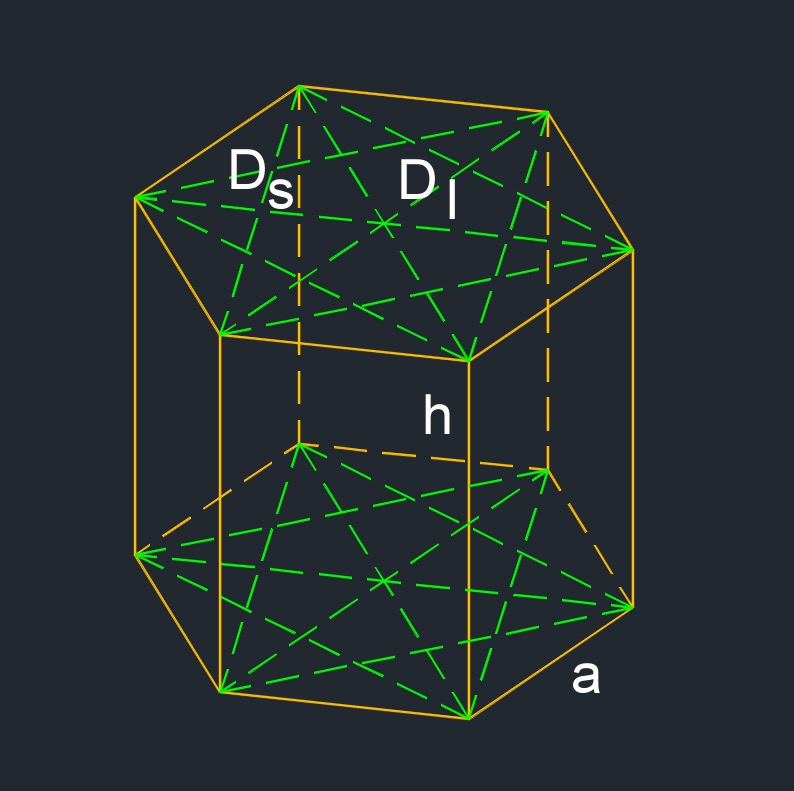
Base Short Diagonal of a Right Hexagon formula Short diagonal does not cross the center point of the hexagon.
$D_s \;=\; \sqrt{3} \cdot a$
Symbol	English	Metric
$D_s$ = short diagonal	$in$	$mm$
$a$ = edge	$in$	$mm$

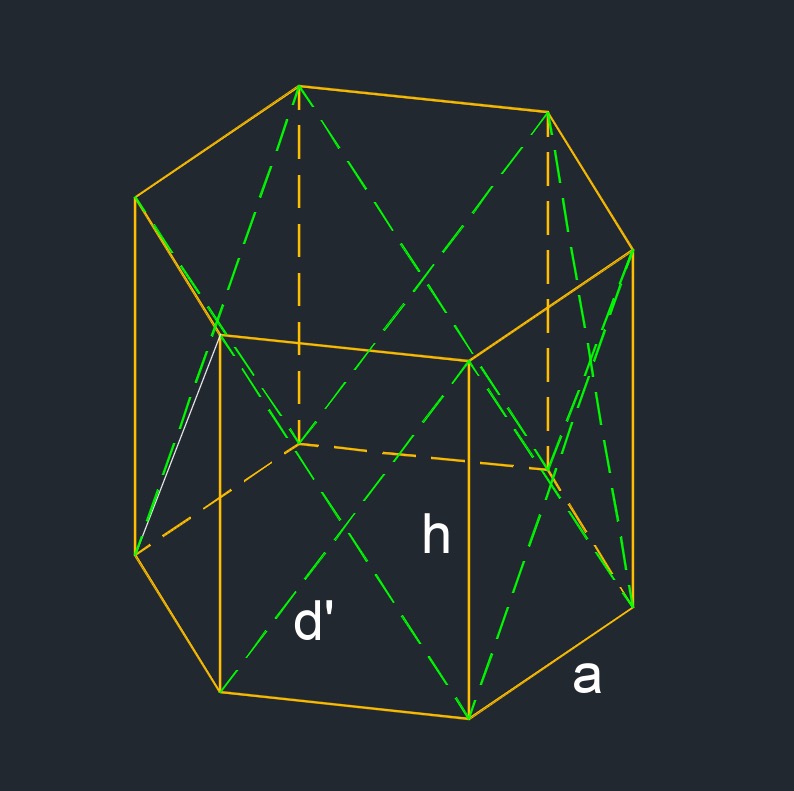
Side Diagonal of a Right Hexagonal Prism formula
$d' \;=\; \sqrt{ a^2 + h^2 }$
Symbol	English	Metric
$d'$ = diagonal	$in$	$mm$
$a$ = edge	$in$	$mm$
$h$ = height	$in$	$mm$

Edge of a Right Hexagonal Prism formulas
$a \;=\; \dfrac{ A_l }{ 6 \cdot h }$ $a \;=\; 3^{1/4} \cdot \sqrt{ 2 \cdot \dfrac{ V }{ 9 \cdot h } }$ $a \;=\; \dfrac{1}{3} \cdot \sqrt{ 3 \cdot h^2 + \sqrt{3} \cdot A_s } - \sqrt{3} \cdot \dfrac {h}{3}$ $a \;=\; 3^{1/4} \cdot \sqrt{2 \cdot \dfrac{ A_b }{ 9 } }$
Symbol	English	Metric
$a$ = edge	$in$	$mm$
$A_b$ = base area	$in^2$	$mm^2$
$h$ = height	$in$	$mm$
$A_l$ = lateral surface area	$in^2$	$mm^2$
$A_s$ = surface area	$in^2$	$mm^2$
$V$ = volume	$in^3$	$mm^3$

Height of a Right Hexagonal Prism formulas
$h \;=\; 2 \cdot \sqrt{ 3 } \cdot \dfrac{ V }{ 9 \cdot a^2 }$ $h \;=\; \dfrac{ A_s }{ 6 \cdot a } - \sqrt{ 3 } \cdot \dfrac{ a }{ 2 }$
Symbol	English	Metric
$h$ = height	$in$	$mm$
$a$ = edge	$in$	$mm$
$A_s$ = surface area	$in^2$	$mm^2$
$V$ = volume	$in^3$	$mm^3$

Lateral Surface Area of a Right Hexagonal Prism formula
$A_l \;=\; 6 \cdot a \cdot h$
Symbol	English	Metric
$A_l$ = lateral surface area	$in^2$	$mm^2$
$a$ = edge	$in$	$mm$
$h$ = height	$in$	$mm$

Surface Area of a Right Hexagonal Prism formula
$A_s \;=\; 6 \cdot a \cdot h + 3 \cdot \sqrt{ 3 } \cdot a^2$
Symbol	English	Metric
$A_s$ = surface area	$in^2$	$mm^2$
$a$ = edge	$in$	$mm$
$h$ = height	$in$	$mm$

Volume of a Right Hexagonal Prism formulas
$V \;=\; \dfrac{ 3 \cdot \sqrt{ 3 } }{ 2 } \cdot a^2 \cdot h$ $V \;=\; 3 \cdot a \cdot b \cdot h$
Symbol	English	Metric
$V$ = volume	$in^3$	$mm^3$
$b$ = center	$in$	$mm$
$a$ = edge	$in$	$mm$
$h$ = height	$in$	$mm$

Similar Articles

Latest Articles