Base Area of a Right Square Pyramid formula |
||
| \( A_b \;=\; a^2 \) | ||
| Symbol | English | Metric |
| \( A_b \) = base area | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |
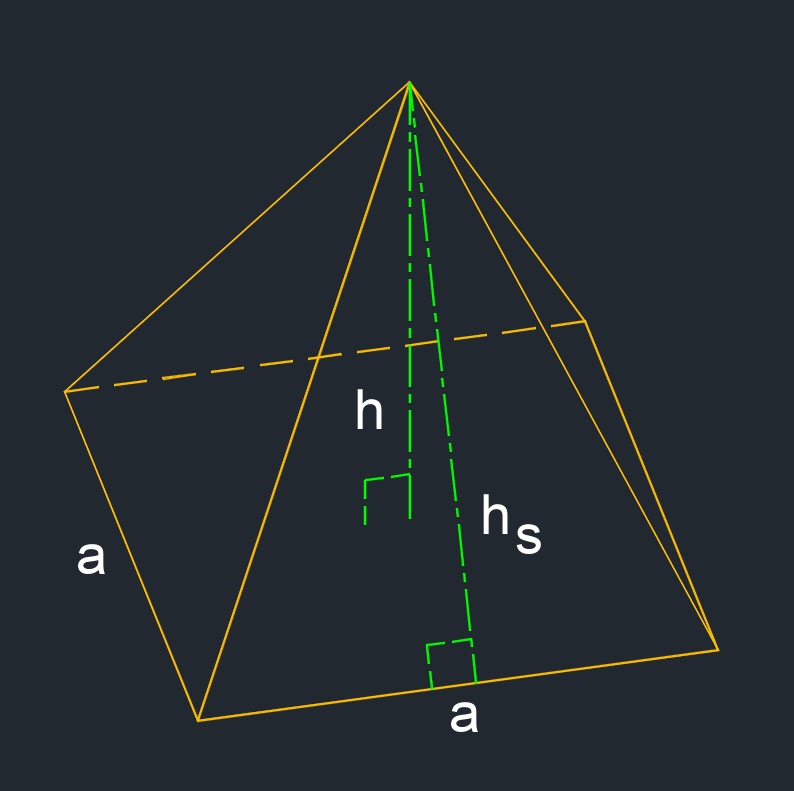
- Right square pyramid (a three-dimensional figure) has a square base and the apex alligned above the center of the base.
- 1 base / 8 edges / 4 faces / 5 vertexs
Height of a Right Square Pyramid formula |
||
| \( h \;=\; \dfrac{1}{2} \cdot \sqrt{ 16\cdot \left( \dfrac{ A_f }{ a } \right)^2 - a^2 } \) | ||
| Symbol | English | Metric |
| \( h \) = height | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
Face Area of a Right Square Pyramid formula |
||
| \( A_f \;=\; \dfrac{a}{2} \cdot \sqrt{ \dfrac{ a^2 }{ 4 } +h^2 } \) | ||
| Symbol | English | Metric |
| \( A_f \) = face area (side) | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
Lateral Surface Area of a Right Square Pyramid formula |
||
| \( A_l \;=\; a \cdot \sqrt{ a^2 + 4 \cdot h^2 } \) | ||
| Symbol | English | Metric |
| \( A_l \) = lateral surface area (sides) | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
Surface Area of a Right Square Pyramid formula |
||
| \( A_s \;=\; a^2 + 2 \cdot a \cdot \sqrt { \dfrac{ a^2 }{ 4 } + h^2 } \) | ||
| Symbol | English | Metric |
| \( A_s \) = surface area (bottom, sides) | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( h \) = edge | \( in \) | \( mm \) |
Volume of a Right Square Pyramid formula |
||
| \( V \;=\; a^2 \cdot \dfrac{h}{3} \) | ||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |