Cube
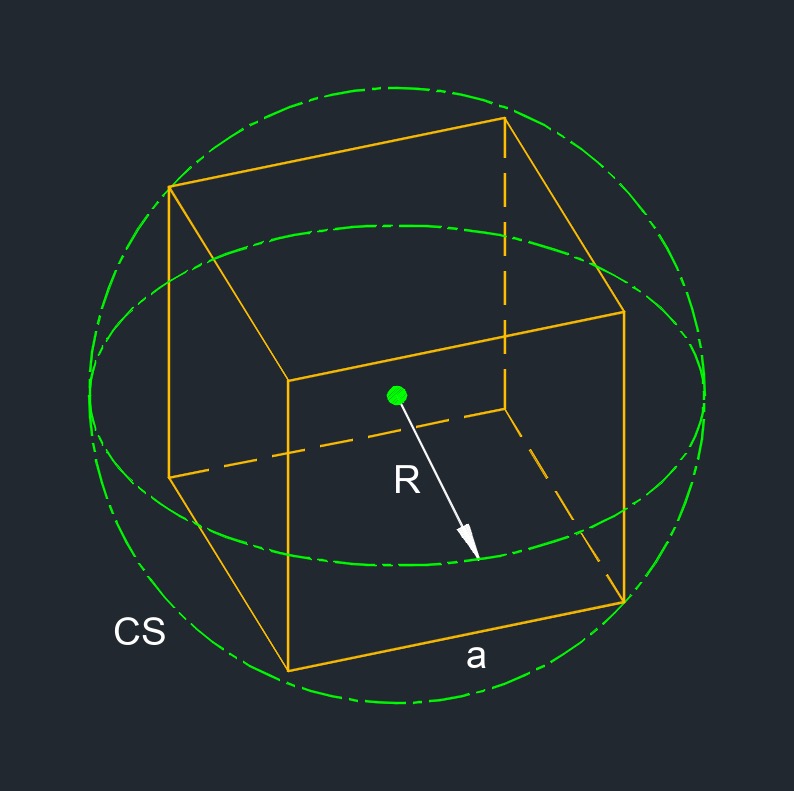
Cube Circumscribed Sphere Radius formula
|
||
| \( R \;=\; \dfrac{ a \cdot \sqrt{ 3 } }{ 2 } \) | ||
| Symbol | English | Metric |
| \( R \) = circumscribed sphere radius | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |
- Cube (a three-dimensional figure) is a regular polyhedron with square faces.
- All edges are the same length.
- All faces are squares
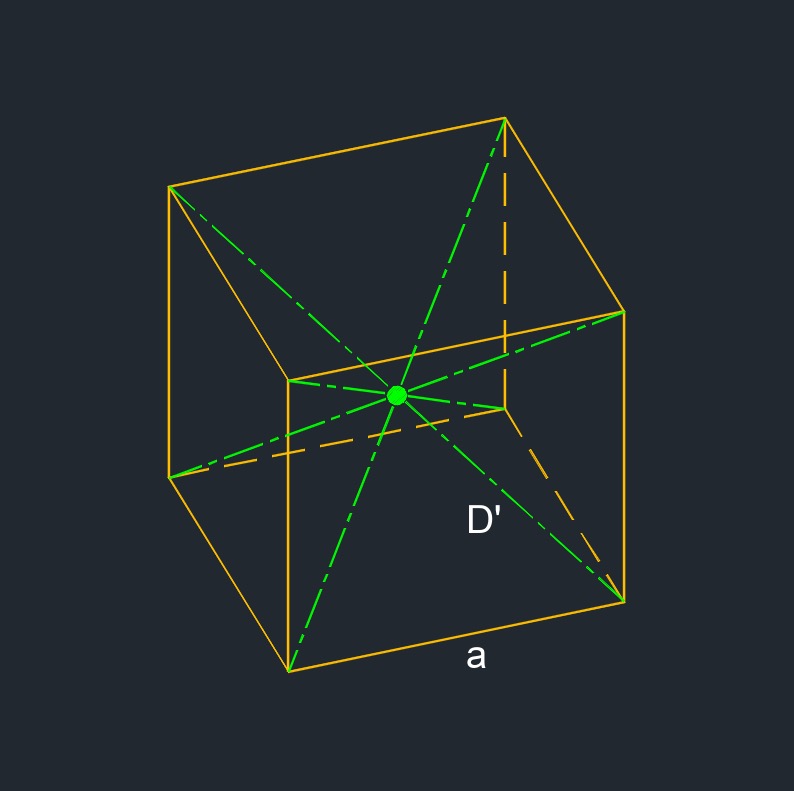
- Diagonal is a line from one vertices to another that is non adjacent.
- Circumscribed sphere is a polyhedron is a sphere that contains the polyhedron and touches each of the ployhedron's vertices.
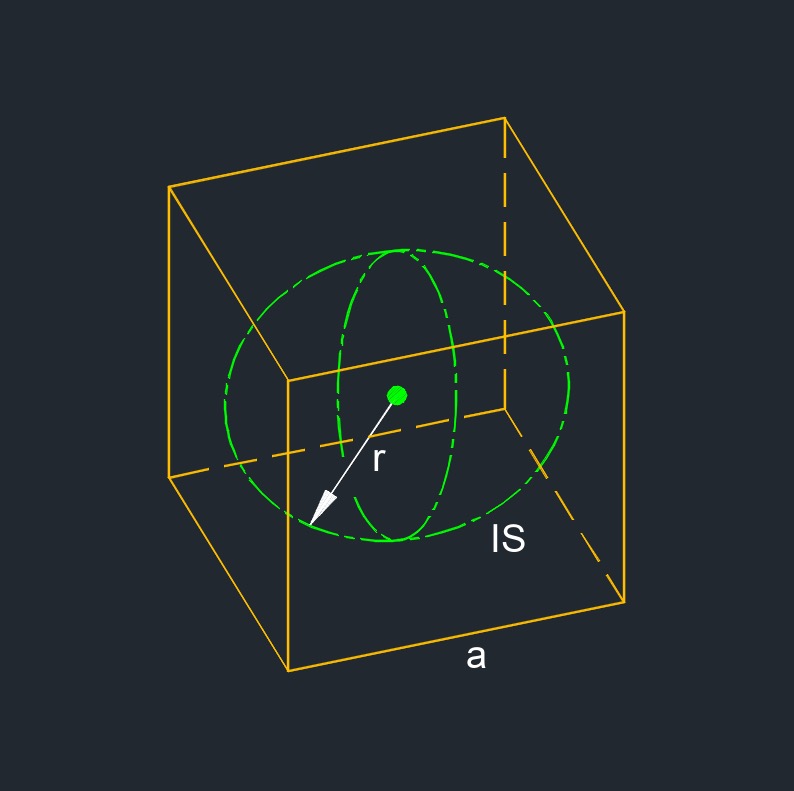
- Inscribed sphere is a convex polyhedron is a sphere that is contained within the polyhedron and tangent to each of the polyhedron's faces.
- Midsphere is a polyhedron is a sphere that is tangent to every edge of the polyhedron.
- 4 base diagonals / 24 face diagonals / 4 space diagonals / 12 edges / 6 faces / 8 vertex
Circumscribed Sphere Volume of a Cube formula
|
||
| \( C_v \;=\; \dfrac{3 }{ 4} \cdot \pi \cdot \left(\dfrac{ a \cdot \sqrt{3} }{ 2 } \right)^3 \) | ||
| Symbol | English | Metric |
| \( C_v \) = circumscribed sphere volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |


Edge of a Cube formulas |
||
|
\( a \;=\; \sqrt{ \dfrac{ A_s }{ 6 } }\) \( a \;=\; V^{1/3} \) \( a \;=\; \sqrt{ 3 } \cdot \dfrac{ D' }{ 3 } \) |
||
| Symbol | English | Metric |
| \( a \) = edge | \( in \) | \( mm \) |
| \( D' \) = space diagonal | \( in \) | \( mm \) |
| \( A_s \) = surface face area | \( in \) | \( mm \) |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
Face Area of a Cube formula |
||
| \( A_{area} \;=\; a^2 \) | ||
| Symbol | English | Metric |
| \( A_{area} \) = face area | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |

Inscribed Radius of a Cube formula
|
||
| \( r \;=\; \dfrac{ a }{ 2 } \) | ||
| Symbol | English | Metric |
| \( r \) = inside radius | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |
Inscribed Sphere Volume of a Cube formula
|
||
| \( I_v \;=\; \dfrac{ 3 }{ 4 } \cdot \pi \cdot \left(\dfrac{ a }{ 2 } \right)^3 \) | ||
| Symbol | English | Metric |
| \( I_v \) = inscribed sphere volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |

Midsphere Radius of a Cube formula
|
||
| \( r_m \;=\; \dfrac{ a }{ 2 } \cdot \sqrt {2} \) | ||
| Symbol | English | Metric |
| \( r_m \) = midsphere radius | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |

Space Diagonal of a Cube formula |
||
| \( D' \;=\; \sqrt {3} \cdot a \) | ||
| Symbol | English | Metric |
| \( D' \) = space diagonal | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |

Surface face Area of a Cube formula |
||
| \( A_s \;=\; 6 \cdot a^2 \) | ||
| Symbol | English | Metric |
| \( A_s \) = surface face area | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |

Surface to volume ratio of a Cube formula |
||
| \( S_v \;=\; \dfrac{ 6 }{ a }\) | ||
| Symbol | English | Metric |
| \( S_v \) = surface to volume ratio | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |

Volume of a Cube formula |
||
| \( V \;=\; a^3 \) | ||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |

Weight of a Cube formula |
||
| \( m \;=\; a^3 \cdot \rho \) | ||
| Symbol | English | Metric |
| \( m \) = mass | \( lbm \) | \( kg \) |
| \( \rho \) (Greek symbol rho) = density | \(lbm\;/\;ft^3\) | \(kg\;/\;m^3\) |
| \( a \) = edge | \( in \) | \( mm \) |

