Sphere
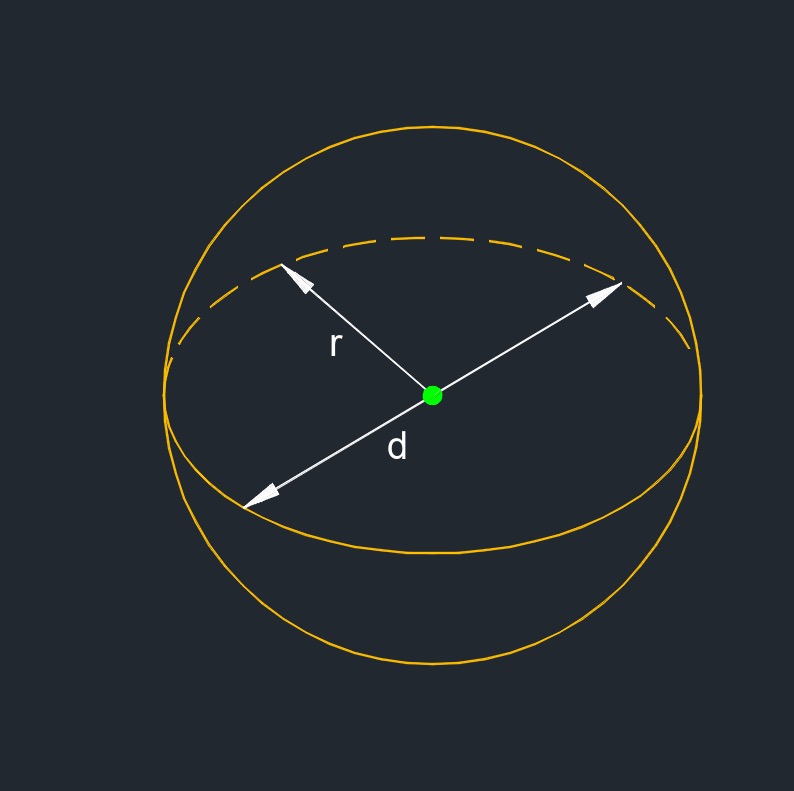
Circumference of a Sphere formula |
||
| \( C \;=\; 2 \cdot \pi \cdot r \) | ||
| Symbol | English | Metric |
| \( C \) = circumference | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
| \( d \) = diameter | \( in \) | \( mm \) |
- Sphere (a three-dimensional figure) has all points equally spaces from a given point of a three dimensional solid.
- Lune of a sphere is the space occupied by a wedge from the center of the sphere to the surface of the sphere.
- Sector of a sphere is the space occupied by a portion of the sphere with the vertex at the center and conical boundary
- Sperical cap is the space occupied by a portion of the sphere cut by a plane.
- See Artical Link - Moment of Inertia of a Sphere
Diameter of a Sphere formula |
||
| \( d \;=\; 2 \cdot r \) | ||
| Symbol | English | Metric |
| \( d \) = diameter | \( in \) | \( mm \) |
| \( r \) = radius | \( in \) | \( mm \) |

Radius of a sphere formula |
||
|
\( r \;=\; \sqrt{ \dfrac{ S }{ 4 \cdot \pi } }\) \( r \;=\; \sqrt{ \dfrac{ 3 }{ 4 } \cdot \dfrac{ V }{ \pi } } \) |
||
| Symbol | English | Metric |
| \( r \) = radius | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( S \) = surface area | \( in^2 \) | \( mm^2 \) |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
Surface Area of a sphere formula |
||
| \( S \;=\; 4 \cdot \pi \cdot r^2 \) | ||
| Symbol | English | Metric |
| \( S \) = surface area | \( in^2 \) | \( mm^2 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Volume of a sphere formula |
||
|
\( V \;=\; \dfrac{4}{3} \cdot \pi \cdot r^3 \) \( V \;=\; \dfrac{ \pi \cdot d^3 }{ 6 }\) |
||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
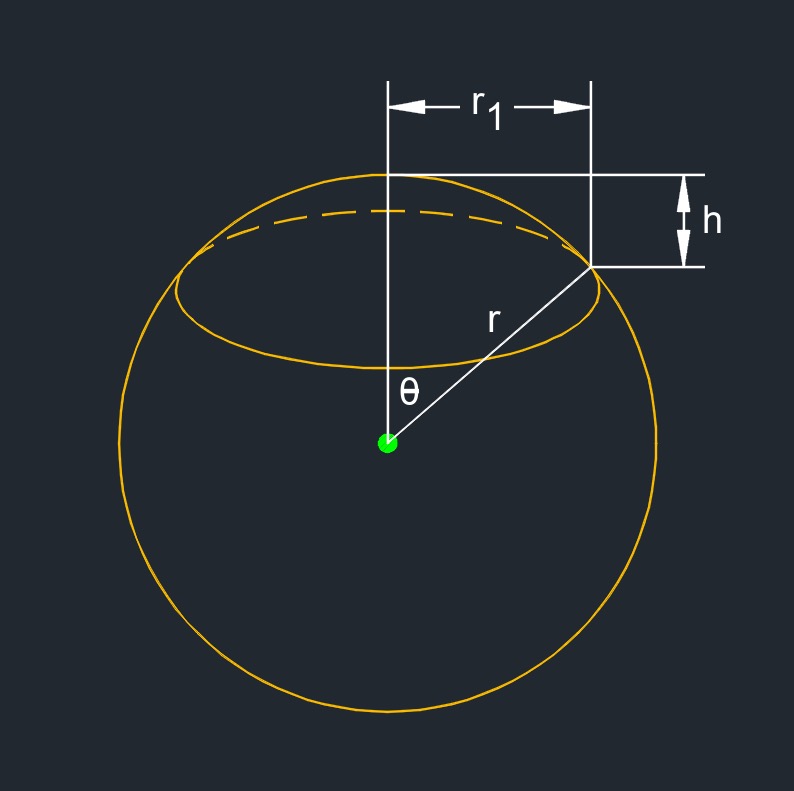
Surface Area of a sphere Cap formula |
||
| \( S \;=\; 2 \cdot \pi \cdot r \cdot h \) | ||
| Symbol | English | Metric |
| \( S \) = surface area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
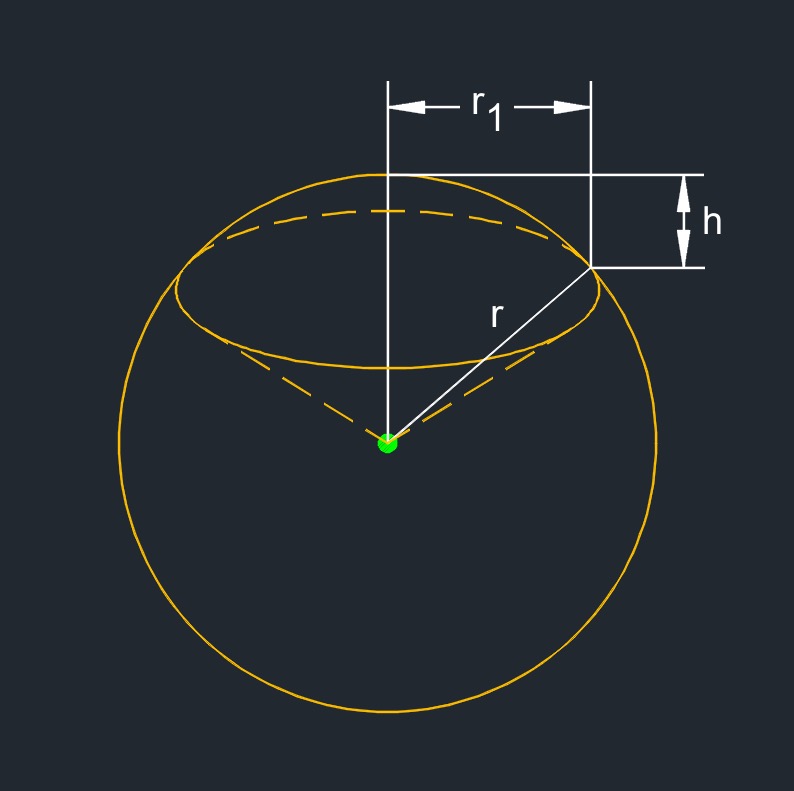
Volume of a sphere Cap formula |
||
|
\( V \;=\; \dfrac {1}{3} \cdot \pi \cdot h^2 \cdot \left( 3 \cdot r - h \right) \) \( V \;=\; \dfrac {1}{6} \cdot \pi \cdot h \cdot \left( 3 \cdot r_1{^2} + h^2 \right) \) |
||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
| \( r_1 \) = radius | \( in \) | \( mm \) |
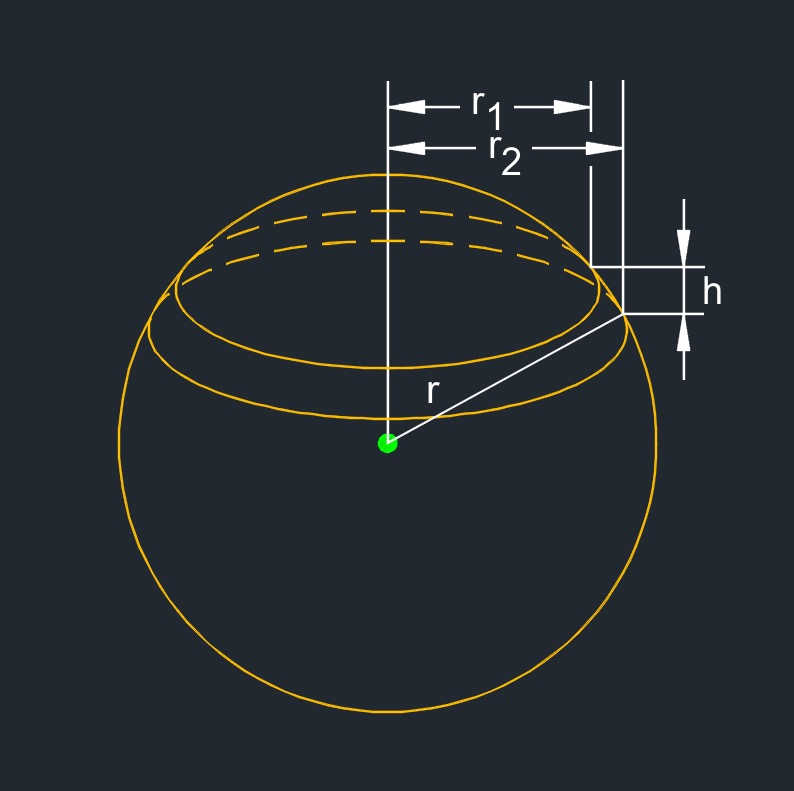
Surface Area of a sphere Segment formula |
||
| \( S \;=\; 2 \cdot \pi \cdot r \cdot h \) | ||
| Symbol | English | Metric |
| \( S \) = surface area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Volume of a sphere Segment formula |
||
| \( V \;=\; \dfrac {1}{6} \cdot \pi \cdot h \cdot \left( 3 r_1{^2} + 3 r_2{^2} + h^2 \right) \) | ||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
| \( r_1 \) = radius | \( in \) | \( mm \) |
| \( r_2 \) = radius | \( in \) | \( mm \) |
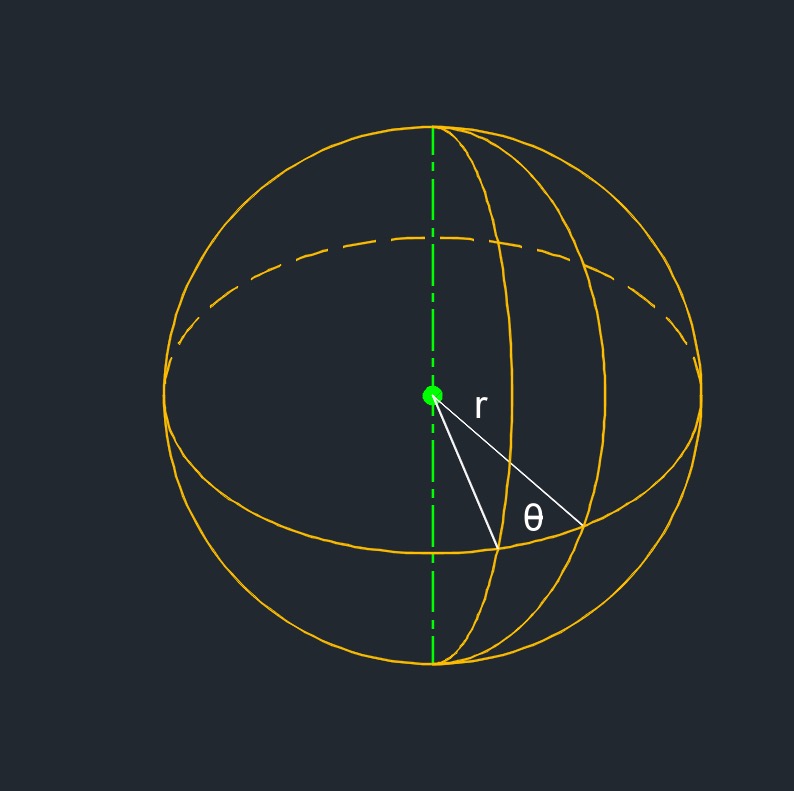
Surface Area of a sphere Wedge formula |
||
| \( S \;=\; \dfrac{ \theta }{ 360 } \cdot 4 \cdot \pi \cdot r^2 \) | ||
| Symbol | English | Metric |
| \( S \) = surface area | \( in^2 \) | \( mm^2 \) |
| \( \theta \) = angle | \( deg \) | \( rad \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Volume of a sphere Wedge formula |
||
| \( V \;=\; \dfrac{ \theta }{ 2 \cdot \pi } \cdot \dfrac{ 4 }{ 3 } \cdot \pi \cdot r^2 \) | ||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( \theta \) = angle | \( deg \) | \( rad \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Volume of a sphere Sector formula |
||
| \( V \;=\; \dfrac {2}{3} \cdot \pi \cdot r^2 \cdot h \) | ||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
| \( r_1 \) = radius | \( in \) | \( mm \) |