Surface Tension
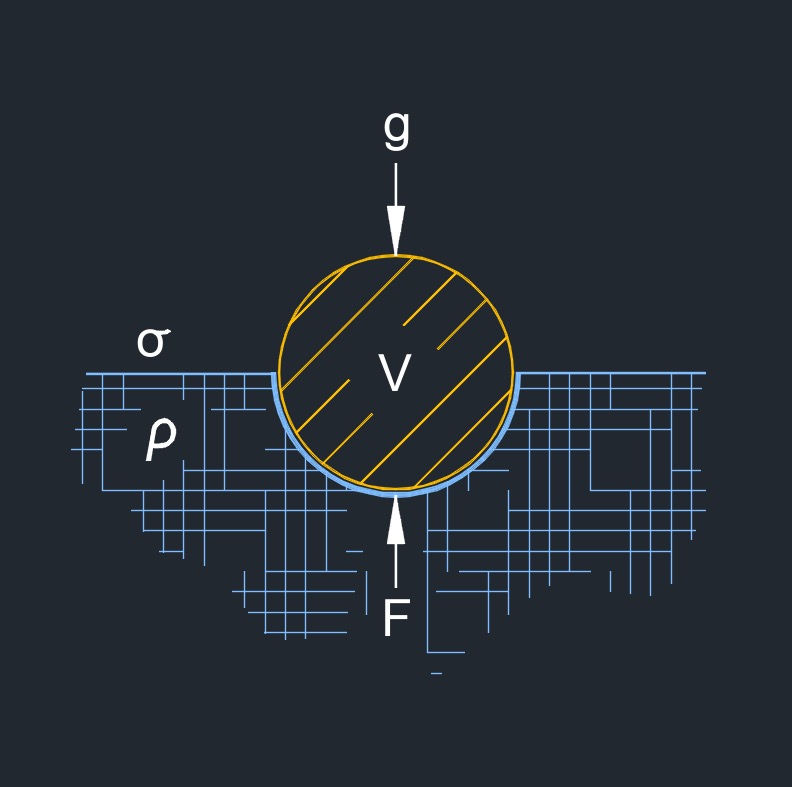Surface tension, abbreviated as \( \sigma \) (Greek symbol sigma), is the force that acts on the surface of a liquid, tending to minimize its surface area. It is caused by the cohesive forces between the liquid molecules, which are stronger at the surface than in the bulk of the liquid.
The surface tension of a liquid is a measure of its ability to resist deformation and is dependent on the type of liquid, temperature, and pressure. Surface tension is responsible for many interesting phenomena, such as the formation of droplets, the shape of soap bubbles, and the ability of insects to walk on water. The surface tension formula is widely used in physics, chemistry, and engineering to describe the behavior of liquids at interfaces, and to design and optimize various applications involving fluid interfaces, such as emulsions, foams, and coatings.
Surface Tension Formula |
||
|
\( \sigma \;=\; \dfrac{ F }{ l }\) (Surface Tension) \( F \;=\; \sigma \cdot l \) \( l \;=\; \dfrac{ F }{ \sigma }\) |
||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Surface Tension | \(lbf - ft\) | \(N - m\) |
| \( F \) = Force Acting Perpendicular to the Surface | \( lbf \) | \(N\) |
| \( l \) = Length of the Surface Over Which the Force Acts | \( ft \) | \( m \) |
