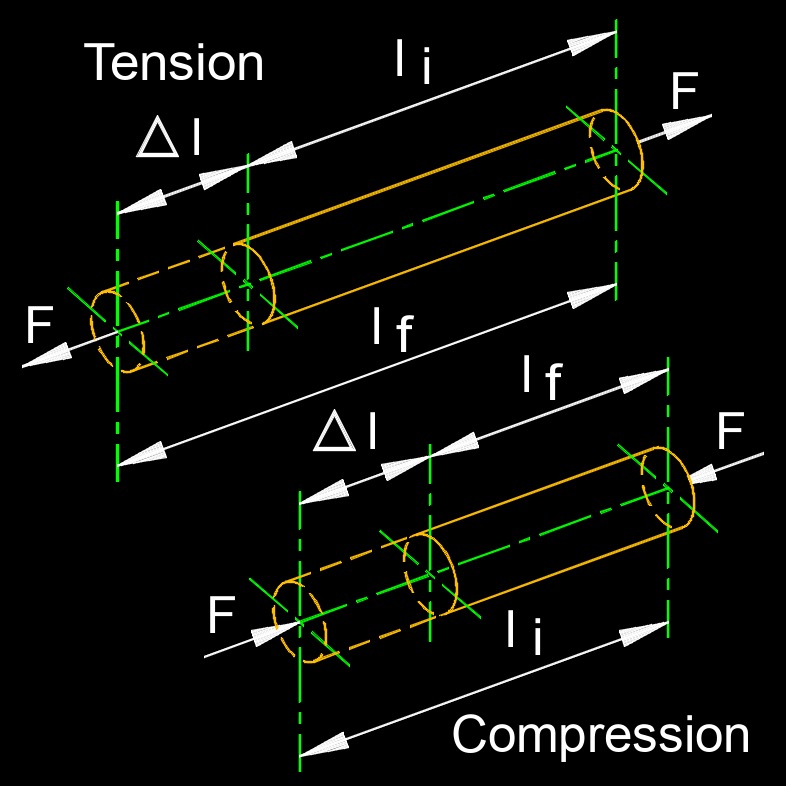
Tension Change in Length Formulas |
||
|
\( \Delta d \;=\; d_i - d_f \) \( \Delta d \;=\; \epsilon_{di} \cdot d_i \) \( \Delta d \;=\; \dfrac{ \mu \cdot \sigma }{ \lambda } \cdot d_i \) \( \Delta d \;=\; \dfrac{ \mu \cdot p }{ \lambda \cdot A } \cdot d_i \) \( \Delta L \;=\; L_f - L_i \) \( \Delta L \;=\; \lambda \cdot L_i \) \( \Delta L \;=\; \dfrac{ \sigma }{ \lambda } \cdot L_i \) \( \Delta L \;=\; \dfrac{ p }{ \lambda \cdot A } \cdot L_i \) |
||
| Symbol | English | Metric |
| \( A \) = Area | \( in^2 \) | \( mm^2 \) |
| \( d_f \) = Final Depth | \( in \) | \( mm \) |
| \( d_i \) = Initial Depth | \( in \) | \( mm \) |
| \( \Delta d \) = Change in Depth | \( in \) | \( mm \) |
| \( \lambda \) (Greek symbol lambda) = Elastic Modulus | \(lbf\;/\;in^2\) | \(Pa\) |
| \( L_f \) = Final Length | \( in \) | \( mm \) |
| \( \Delta L \) = Change in Length | \( in \) | \( mm \) |
| \( L \) = Length Under Consideration | \( in \) | \( mm \) |
| \( \mu \) (Greek symbol mu) = Poisson's Ratio | \( dimensionless \) | \( dimensionless \) |
| \( p \) = Pressure Under Consideration | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \epsilon \) (Greek symbol epsilon) = Strain | \(in\;/\;in\) | \(mm\;/\;mm\) |
| \( \sigma \) (Greek symbol sigma) = Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \sigma_t \) (Greek symbol sigma) = Tensile Stress | \(lbf\;/\;in^2\) | \(Pa\) |
