Skip to main content

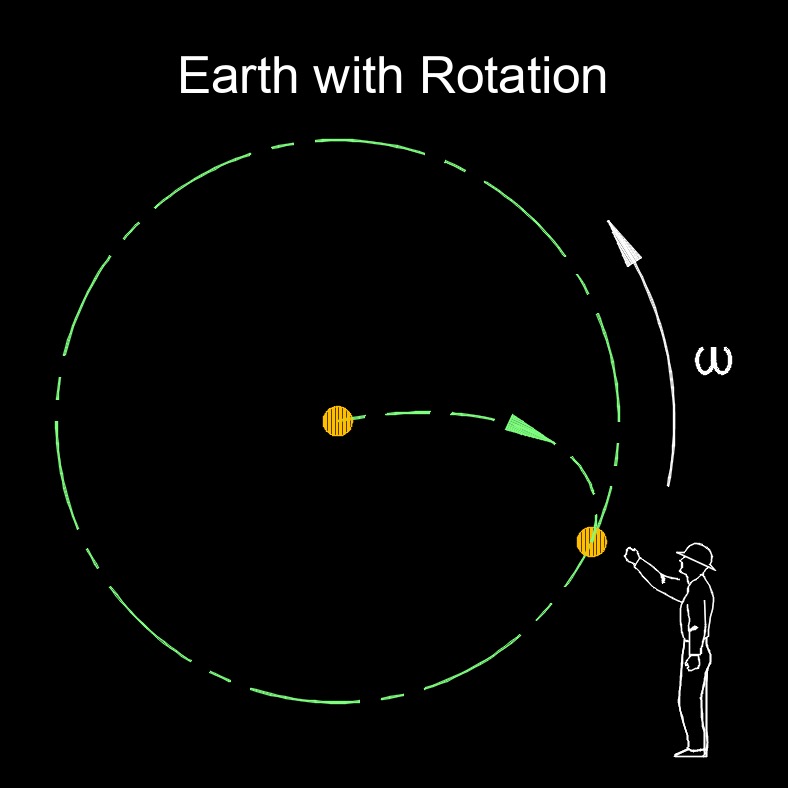
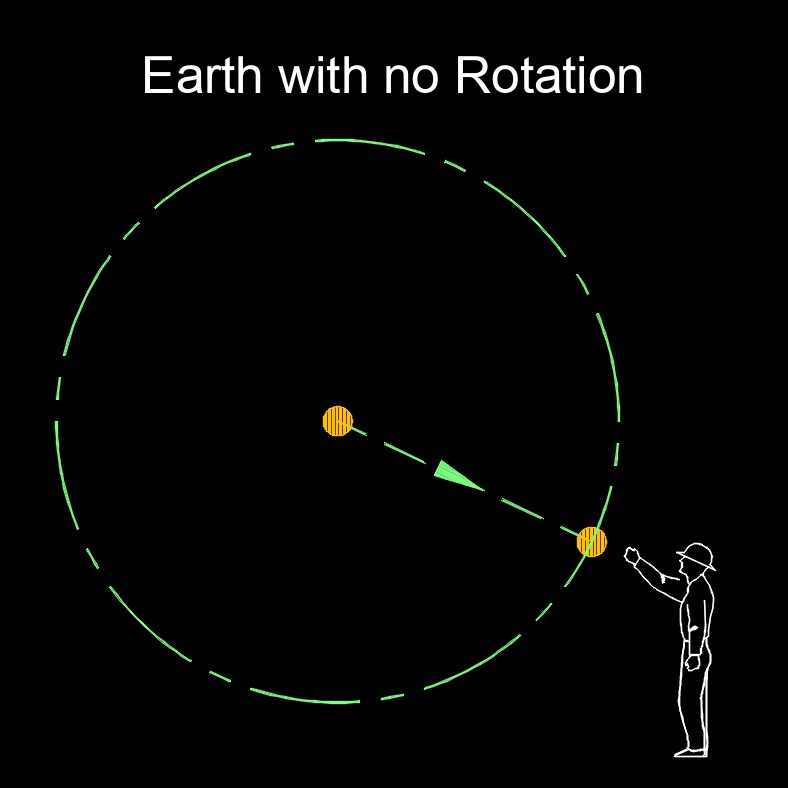
Coriolis Force

 

Coriolis Force Formula

\( F_c \;=\;  - \; ( 2 \cdot m \cdot ( \omega \cdot v_t ) \;) \)     (Coriolis Force)

\( m \;=\; -  \left( \dfrac{ F_c }{ 2 \cdot  ( \omega \cdot v_t ) } \right) \)

\( \omega \;=\; -  \left( \dfrac{ F_c }{ 2 \cdot  ( m \cdot v_t ) } \right) \)

\( v_t \;=\; -  \left( \dfrac{ F_c }{ 2 \cdot  ( m \cdot \omega ) } \right) \)
Symbol English Metric
\( F_c \) = Coriolis Force \(lbf\) \(N\)
\( m \) = Mass \(lbm\) \(kg\)
\( \omega \)   (Greek symbol omega) = Angular Velocity \(deg\;/\;sec\) \(rad\;/\;s\)
\( v_t \) = Tangential Velocity \(ft\;/\;sec\) \(m\;/\;s\)

Coriolis force, abbreviated as \(F_c\), also called Coriolis effect or Coriolis acceleration, is a fictitious force that appears to act on objects in a rotating frame of reference, such as the Earth.  The Coriolis force arises due to the rotation of the Earth.  As the Earth spins on its axis, different points on the Earth's surface are moving at different speeds depending on their distance from the axis of rotation.  This difference in rotational velocity causes objects that move horizontally across the Earth's surface to appear to be deflected from their straight line paths.  It is a fundamental concept in meteorology, oceanography, and the study of the Earth's dynamics.

coriolis force with rotation 1

coriolis force no rotation 1

 

 

 

 

 

Key Points about Coriolis Force
Deflection to the right in the Northern Hemisphere and to the left in the Southern Hemisphere  -  In the Northern Hemisphere, objects moving horizontally will be deflected to the right of their intended path, while in the Southern Hemisphere, they will be deflected to the left.  This deflection is a consequence of the Earth's rotation.
Strength varies with latitude  -  The Coriolis force is strongest at the poles and weakest at the equator.  Near the poles, the rotational speed of the Earth is much lower, so the Coriolis force has a greater effect on moving objects.  Near the equator, where the rotational speed is highest, the Coriolis force is weaker.
Does not affect objects moving vertically  -  The Coriolis force only affects objects that are in motion horizontally.  It has no influence on objects moving vertically (up or down).
Important in meteorology and oceanography  -  The Coriolis force plays a crucial role in the formation and movement of weather systems, ocean currents, and the circulation of the atmosphere.  It influences the direction of winds, the rotation of hurricanes, and the behavior of ocean currents. 

Piping Designer Logo 1