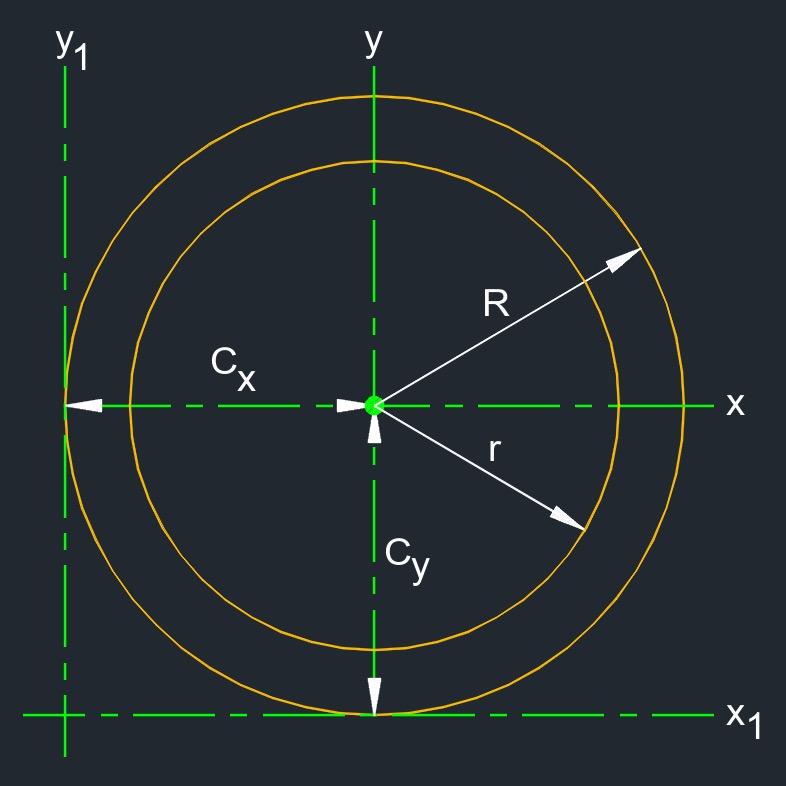
Radius of Gyration of a Hollow Circle formulas |
||
|
\( k_{x} \;=\; \frac{1}{2} \cdot \sqrt { R^2 + r^2 } \) \( k_{y} \;=\; \frac{1}{2} \cdot \sqrt { R^2 + r^2 } \) \( k_{z} \;=\; \dfrac{ \sqrt{ 2 } }{ 2 } \cdot \sqrt{ R^2 + r^2 } \) \( k_{x1} \;=\; \frac{1}{2} \cdot \sqrt{ 5 \cdot R^2 + r^2 } \) \( k_{y1} \;=\; \frac{1}{2} \cdot \sqrt{ 5 \cdot R^2 + r^2 } \) \( k_{z1} \;=\; \dfrac{ \sqrt{ 2 } }{ 2 } \cdot \sqrt{ 5 \cdot R^2 + r^2 } \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( r \) = inside radius | \( in \) | \( mm \) |
| \( R \) = outside radius | \( in \) | \( mm \) |
