Angular Displacement When Angular Velocity is Constant Formula |
||
|
\( \theta_d \;=\; \omega \cdot t \) (Angular Displacement when Angular Velocity is Constant) \( \omega \;=\; \dfrac{ \theta_d }{ t }\) \( t \;=\; \dfrac{ \theta_d }{ \omega }\) |
||
| Symbol | English | Metric |
| \(\theta_d \) (Greek symbol theta) = Angular Displacement | \(deg\) | \(rad\) |
| \( \omega \) (Greek symbol omega) = Constant Angular Velocity | \(\deg \;/\; sec\) | \(rad \;/\; s\) |
| \( t \) = Time | \(sec\) | \(s\) |
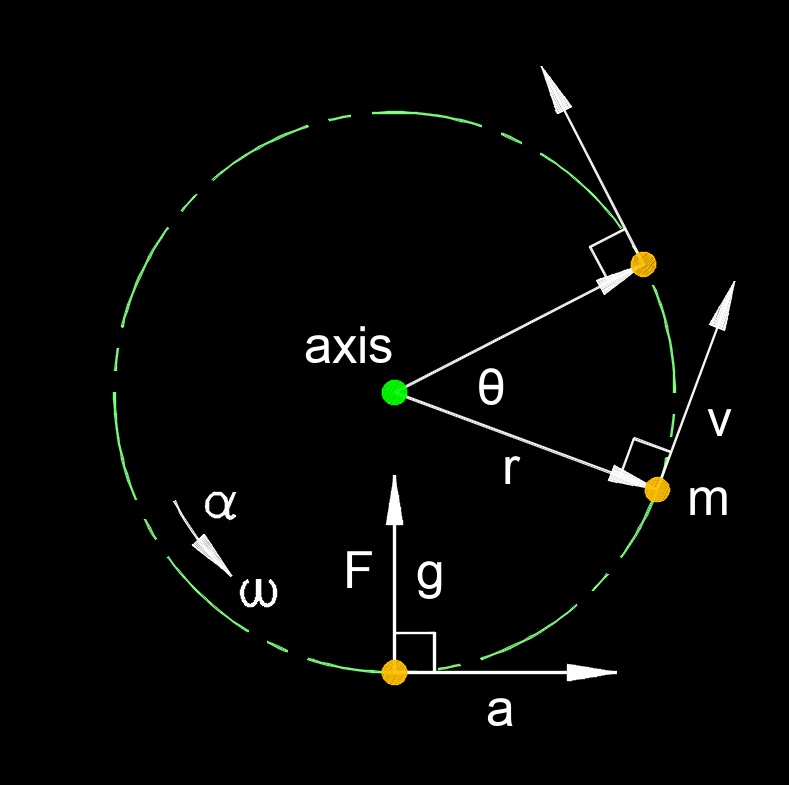Angular displacement when angular velocity is constant, abbreviated as \( \theta_d \), is the change in angular position of a rotating object when it spins at a steady rate without speeding up or slowing down. In this case, the angular acceleration is zero, meaning the rate of rotation remains uniform throughout the motion. This formula shows that when an object rotates at a constant speed, its angular displacement increases linearly with time. For example, if a wheel spins at a constant angular velocity, the longer it rotates, the greater the angular distance it covers.
