Bend Allowance Formula |
||
|
\( BA \;=\; \dfrac{ \theta \cdot \pi }{180 } \cdot ( r + K \cdot t ) \) (Bend Allowance) \( \theta \;=\; \dfrac{ BA \cdot 180 }{ \pi \cdot ( r + K \cdot t ) }\) \( r \;=\; \dfrac{ BA \cdot 180 }{ \theta \cdot \pi } - K \cdot t \) \( K \;=\; \dfrac{ \dfrac{ BA \cdot 180 }{ \theta \cdot \pi } - r }{ t }\) \( t \;=\; \dfrac{ \dfrac{ BA \cdot 180 }{ \theta \cdot \pi } - r }{ K } \) |
||
| Symbol | English | Metric |
| \( BA \) = Bend Allowance | \(in\) | \(mm\) |
| \( \theta \) (Greek symbol theta) = Bend Angle | \(deg\) | \(rad\) |
| \( r \) = Inside Radius | \(in\) | \(mm\) |
| \( K \) = K-factor | \(dimensionless\) | \(dimensionless\) |
| \( t \) = Material Thickness | \(in\) | \(mm\) |
Bend allowance, abbreviated as BA, is the length of the arc through the bend area at the neutral axis. It is the amount of material stretching or elongating as a result of bending operations in pipe or sheet metal fabrication. When a metal sheet is bent, it experiences deformation and elongation along the inner radius of the bend, while the outer surface compresses. This deformation results in changes to the sheet's dimensions, and the bend allowance quantifies these changes.
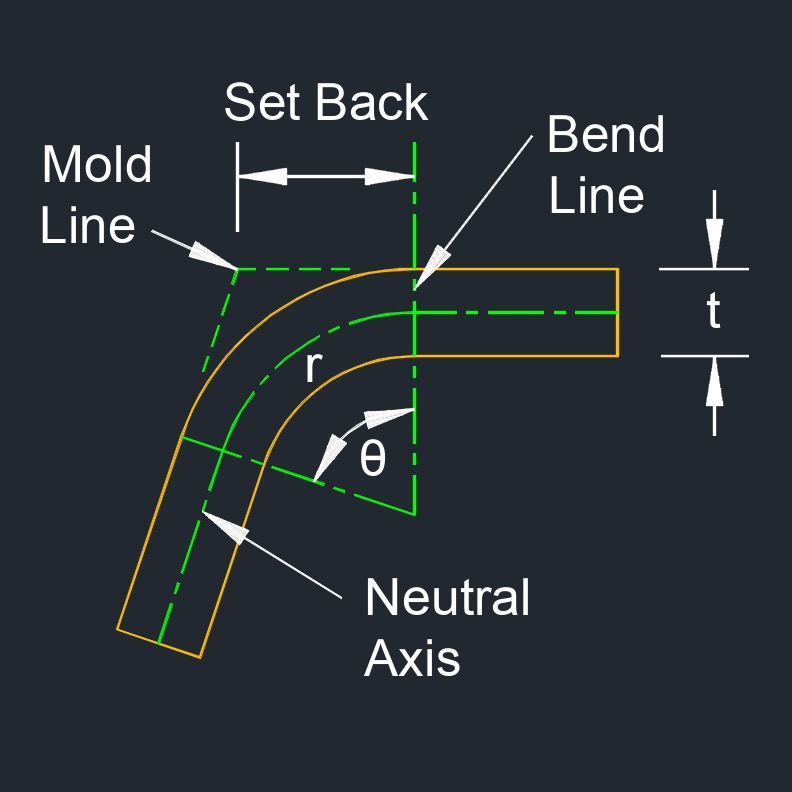
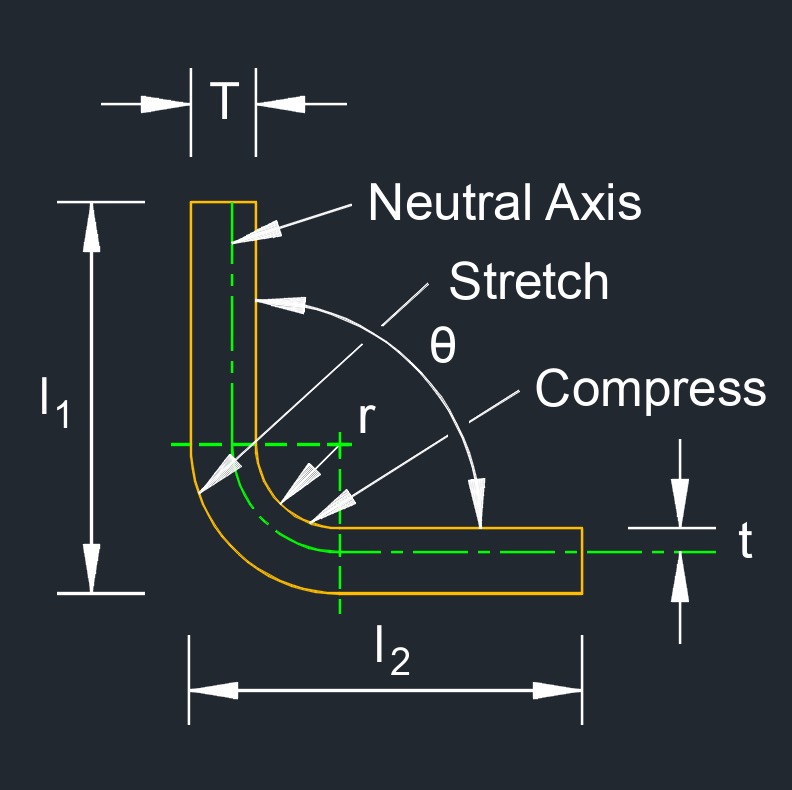
In other words, when a sheet metal piece is bent, the actual length of the material along the neutral axis (the centerline of the bend) increases due to the stretching that occurs on the inner surface of the bend. This elongation needs to be accounted for when designing and cutting the original flat sheet, especially when precise dimensions are crucial for the final product.
Bend Allowance Formula |
||
| \( BA \;=\; \theta \cdot \dfrac{ \pi }{180 } \cdot ( r + K \cdot t ) \) | ||
| Symbol | English | Metric |
| \( BA \) = Bend Allowance | \(in\) | \(mm\) |
| \( \theta \) (Greek symbol theta) = Bend Angle | \(deg\) | \(rad\) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = Inside Radius | \(in\) | \(mm\) |
| \( K \) = K-factor | \(dimensionless\) | \(dimensionless\) |
| \( t \) = Material Thickness | \(in\) | \(mm\) |
Bend allowance is an important factor to consider in sheet metal design and manufacturing, as it helps determine the initial size of the flat sheet that needs to be cut before bending, in order to achieve the desired dimensions in the finished bent piece. Different materials and bending processes might have varying degrees of bend allowance, so accurate calculation and consideration are essential to ensure the final product matches the intended specifications.
