Bend Deduction
Bend Deduction Formula |
||
| \( BD \;=\; 2 \cdot \left( r \;+\; t \right) \cdot tan \left( \dfrac{ \theta}{2} - BA \right) \) | ||
| Symbol | English | Metric |
| \( BD \) = bend deduction | \(in\) | \(mm\) |
| \( r \) = inside radius | \(in\) | \(mm\) |
| \( t \) = material thickness | \(in\) | \(mm\) |
| \( \theta \) (Greek symbol theta) = bend angle | \(deg\) | \(rad\) |
| \( BA \) = bend allowance | \(in\) | \(mm\) |
Bend deduction, abbreviated as \(BA\), describe the amount by which the sum of the lengths of the two legs of a bent metal part is reduced due to the bending process. When a metal sheet or pipe is bent to create an angle or a bend, the material on the inside of the bend compresses, while the material on the outside stretches. This results in a change in the overall length of the material.
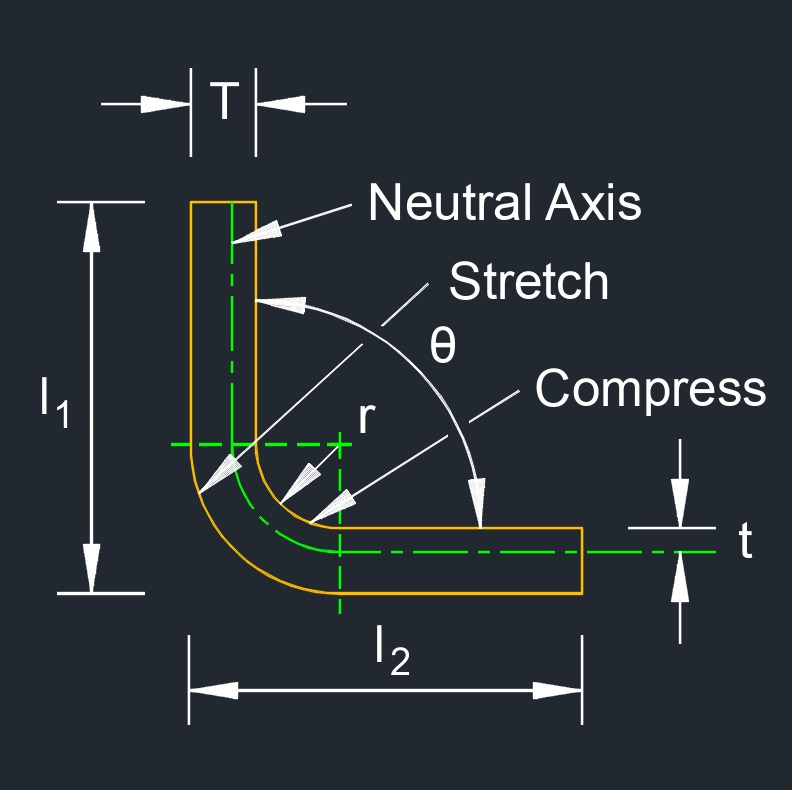
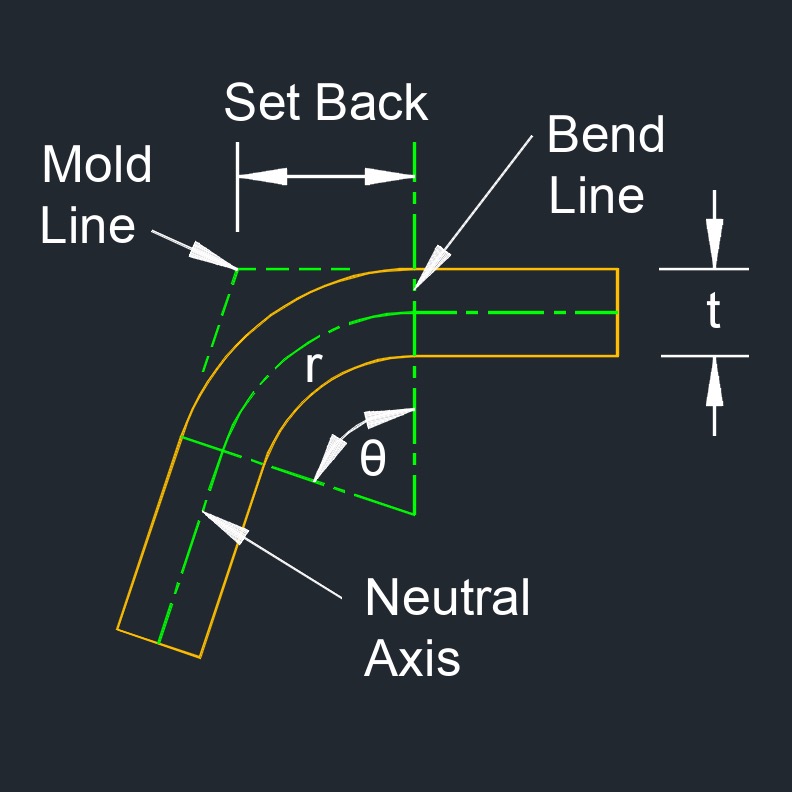
Bend deduction is important to consider when designing and fabricating parts that require accurate dimensions after bending, especially in applications where precision and tight tolerances are critical. The concept of bend deduction is used to calculate the flat pattern length before bending, which helps ensure that the final bent part meets the desired specifications.
The formula to calculate bend deduction depends on various factors, including the material's properties, bend angle, bend radius, and thickness of the material. The formula can be more complex for certain types of bends, such as air bends, where the material's behavior during bending is different.

