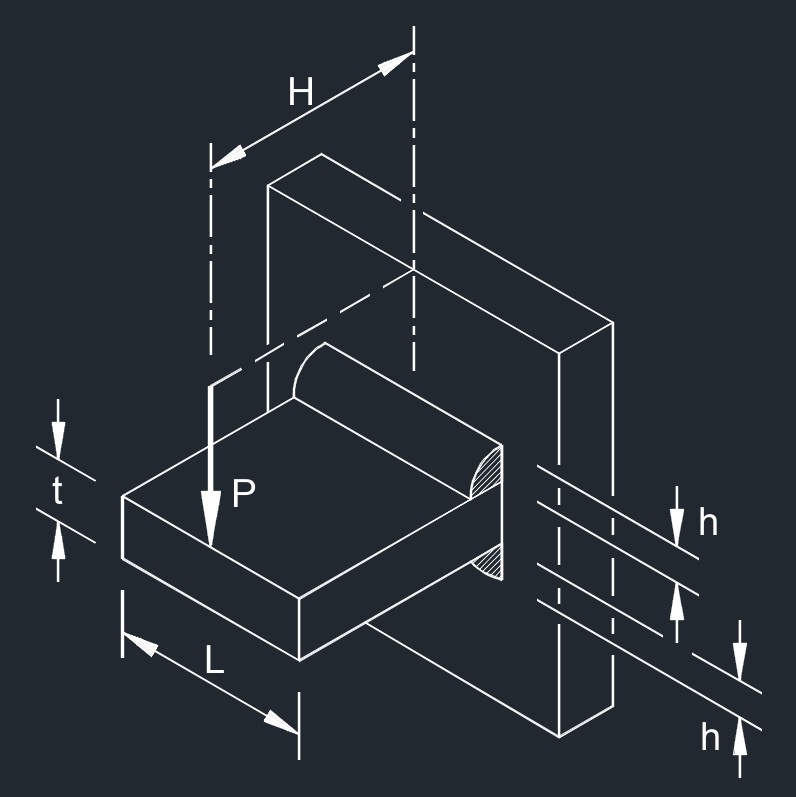
Tee Plate Welds
- See Article - Welded Stress and Strain Connections
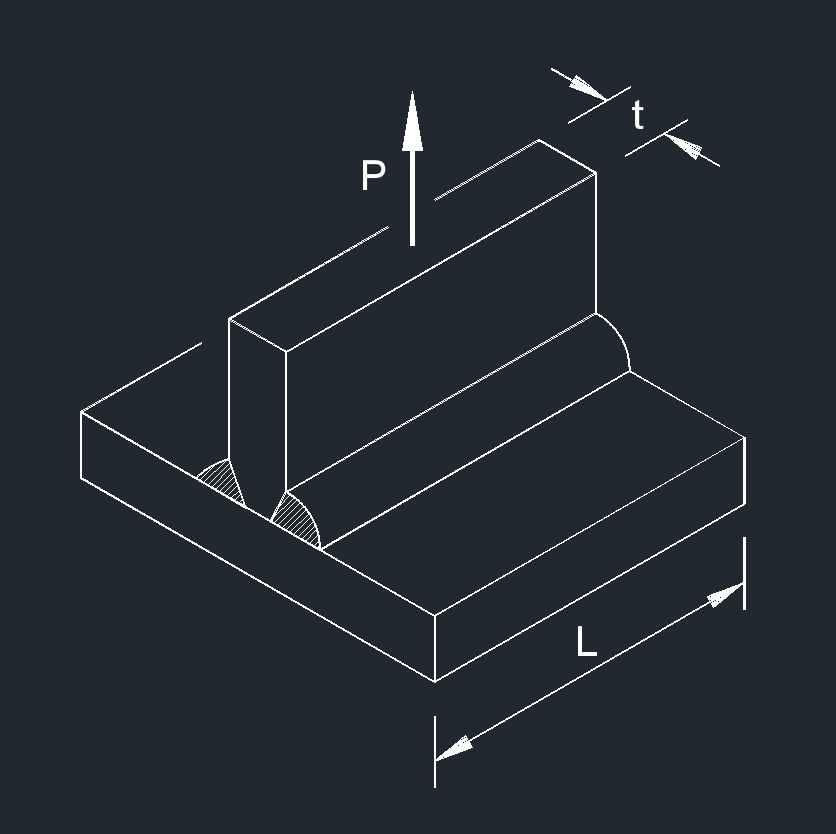
Axial Force on CJP Fillet Weld formula
|
||
| \( \sigma \;=\; \dfrac{ P }{ t \cdot L }\) | ||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
| \( t \) = Plate Thickness | \( in \) | \( mm \) |
| \( P \) = Total Axial Force | \( lbf \) | \( N \) |
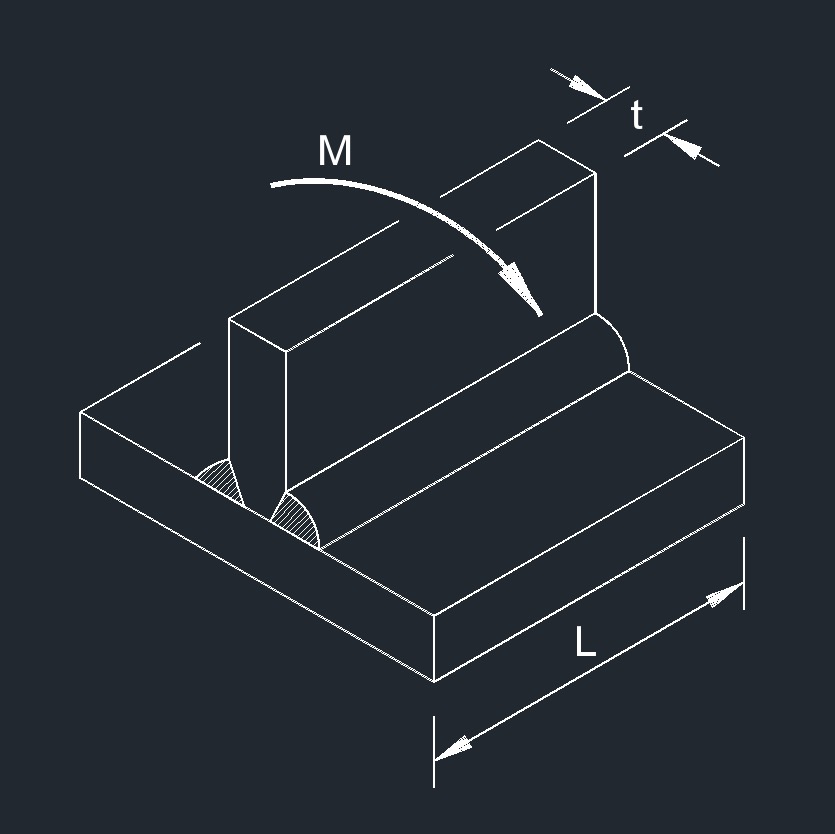
Bending Moment on CJP Fillet Weld formula
|
||
| \( \sigma \;=\; \dfrac{ 6 \cdot M }{ L \cdot t^2 }\) | ||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( M \) = Bending Moment | \(lbf\;/\;sec\) | \(kg-m\;/\;s\) |
| \( t \) = Plate Thickness | \( in \) | \( mm \) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
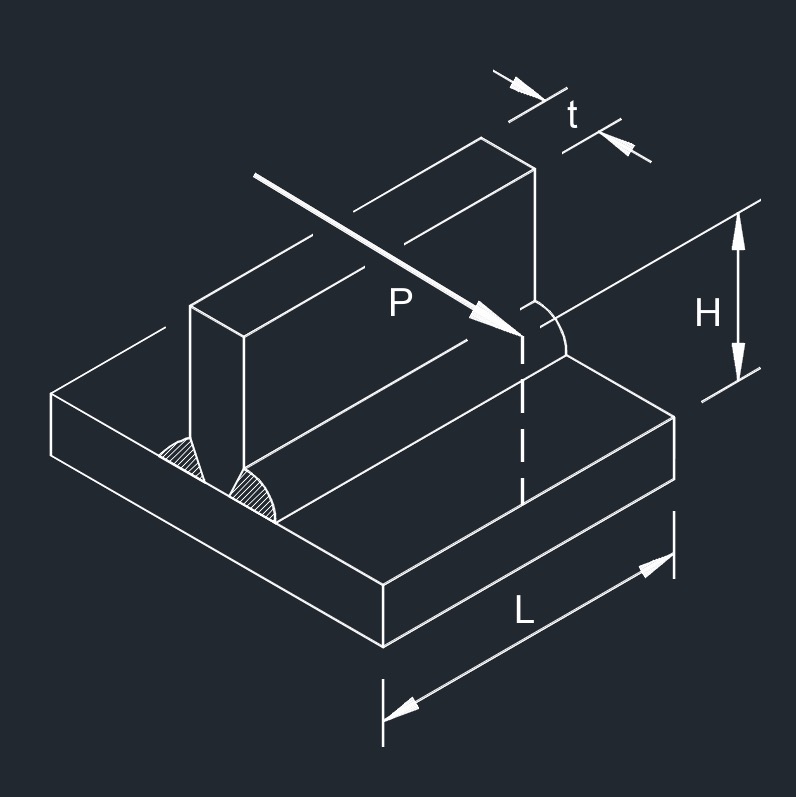
Perpendicular Force on CJP Fillet Weld formulas
|
||
|
\( \sigma \;=\; \dfrac{ 6 \cdot P \cdot H }{ L \cdot t^2 }\) \( \tau \;=\; \dfrac{ P }{ L \cdot t }\) |
||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \tau \) (Greak symbol tau) = Shear Stres | \(lbf\;/\;in^2\) | \(Pa\) |
| \( H \) = Height of Lever Arm | \( in \) | \( mm \) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
| \( t \) = Plate Thickness | \( in \) | \( mm \) |
| \( P \) = Total Applied Force | \( lbf \) | \( N \) |
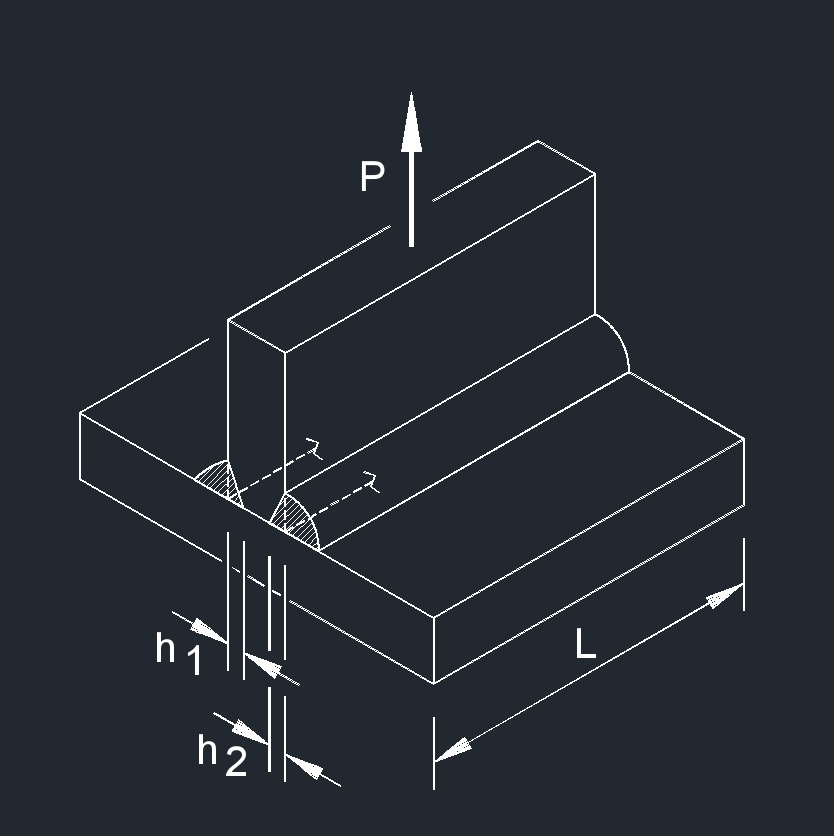
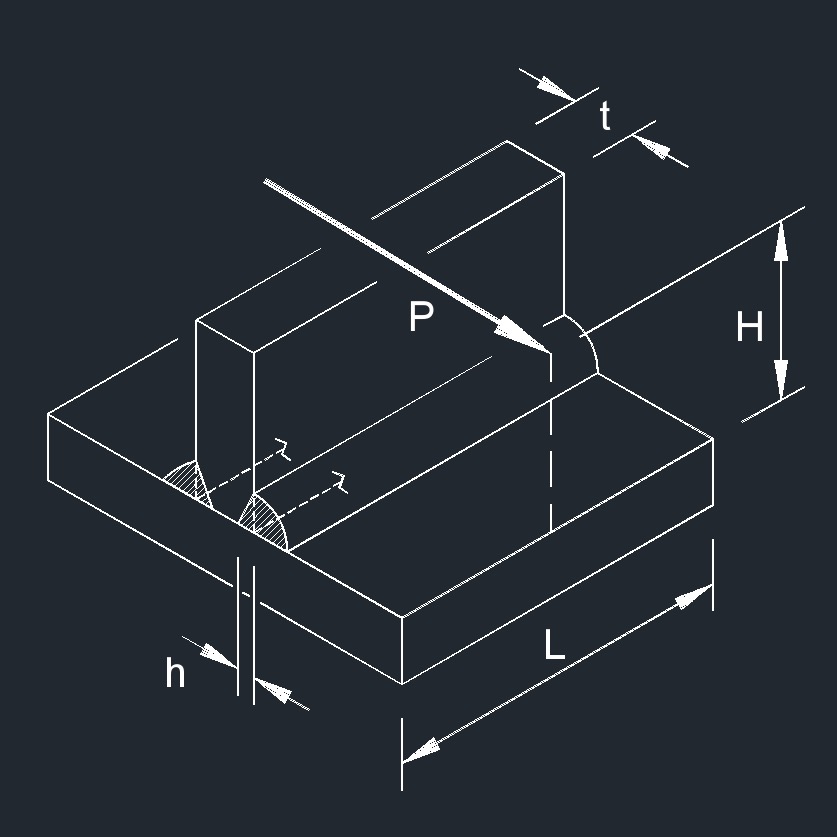
Axial Force on CJP Fillet Weld formula
|
||
| \( \sigma \;=\; \dfrac{ P }{ ( h_1 + h_2) \cdot L }\) | ||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
| \( P \) = Total Applied Force | \( lbf \) | \( N \) |
| \( h_1 \) = Weld Penetration | \( in \) | \( mm \) |
| \( h_2 \) = Weld Penetration | \( in \) | \( mm \) |
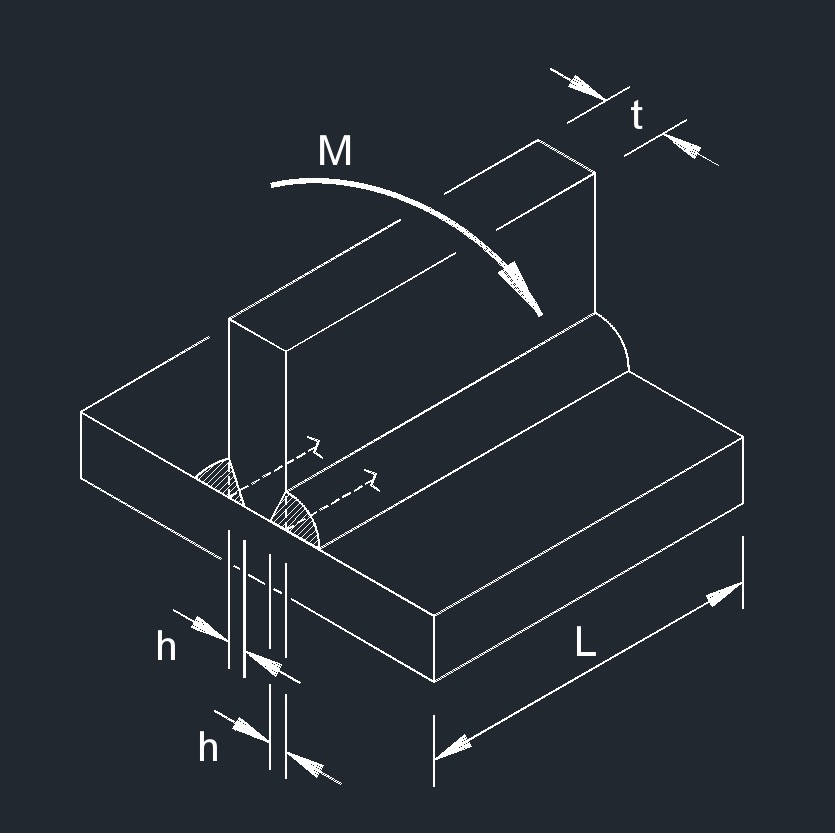
Bending Moment on CJP Fillet Weld formula
|
||
| \( \sigma \;=\; \dfrac{ 3 \cdot t \cdot M }{ L \cdot h \cdot ( 3 \cdot t^2 - 6 \cdot t \cdot h + 4 \cdot h^2 ) }\) | ||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( M \) = Bending Moment | \(lbf\;/\;sec\) | \(kg-m\;/\;s\) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
| \( t \) = Plate Thickness | \( in \) | \( mm \) |
| \( h \) = Weld Penetration | \( in \) | \( mm \) |
Perpendicular Force on CJP Fillet Weld formulas
|
||
|
\( \sigma \;=\; \dfrac{ 3 \cdot t \cdot P \cdot H }{ L \cdot h \cdot ( 3 \cdot t^2 - 6 \cdot t \cdot h + 4 \cdot h^2 ) }\) \( \tau \;=\; \dfrac{ P }{ 2 \cdot L \cdot h } \) |
||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \tau \) (Greak symbol tau) = Shear Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( H \) = Height of Lever Arm | \( in \) | \( mm \) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
| \( t \) = Plate Thickness | \( in \) | \( mm \) |
| \( P \) = Total Applied Force | \( lbf \) | \( N \) |
| \( h \) = Weld Penetration | \( in \) | \( mm \) |
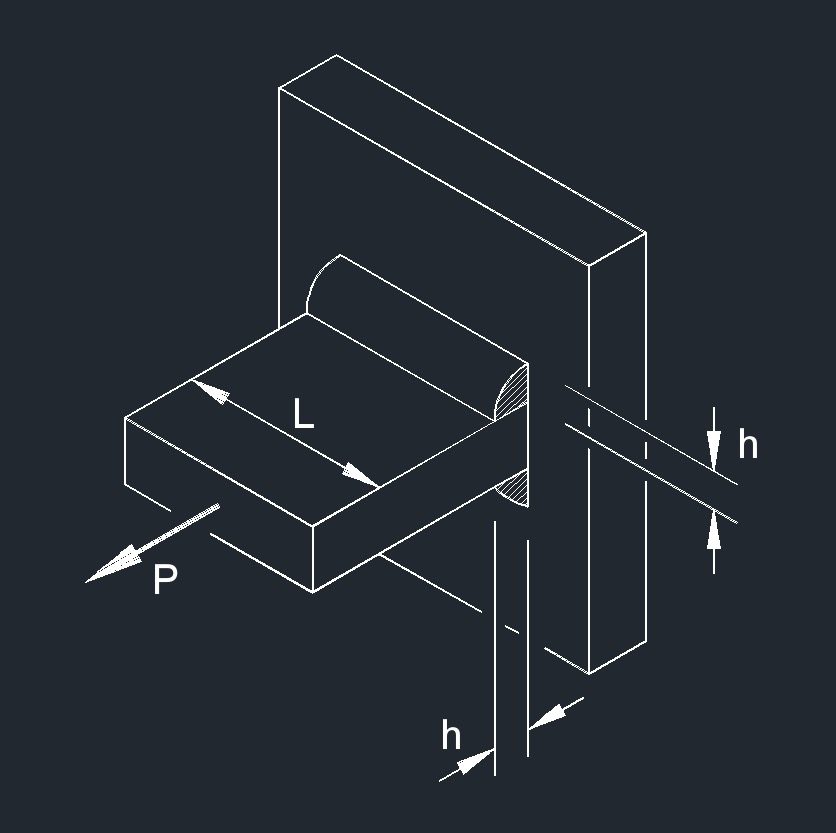
Axial Force on PJP Fillet Weld formula
|
||
| \( \sigma \;=\; \dfrac{ 0.707 \cdot P }{ h \cdot L }\) | ||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( h \) = Weld Thickness | \( in \) | \( mm \) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
| \( P \) = Total Applied Force | \( lbf \) | \( N \) |
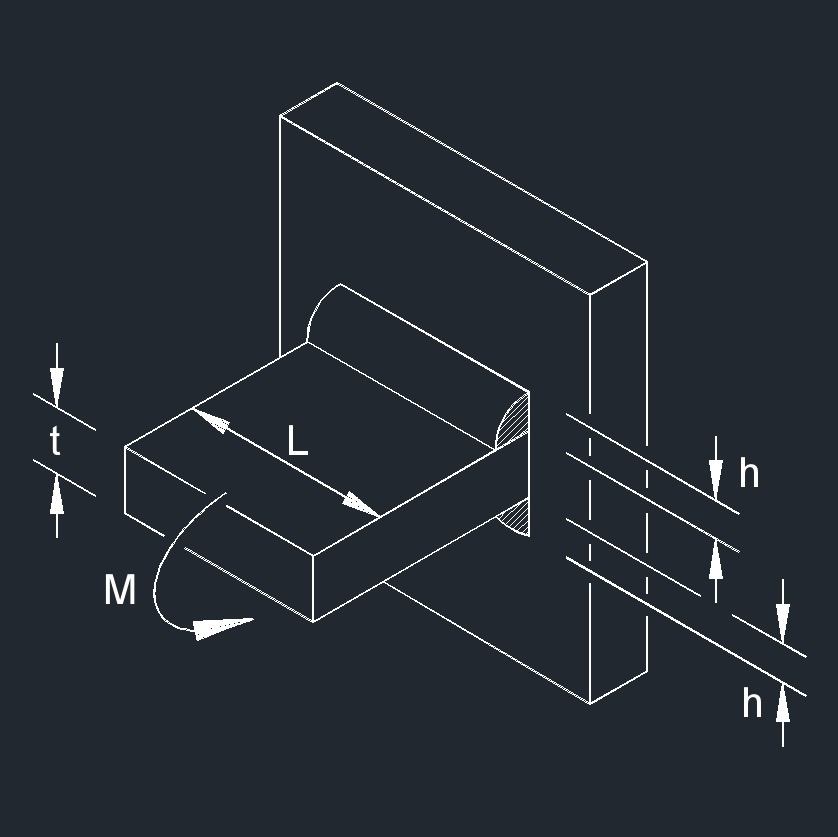
Bending Moment on PJP Fillet Weld formula
|
||
| \( \sigma \;=\; \dfrac{ 1.414 \cdot M }{ h \cdot L \cdot ( t + h ) } \) | ||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( M \) = Bending Moment | \(lbf\;/\;sec\) | \(kg-m\;/\;s\) |
| \( t \) = Plate Thickness | \( in \) | \( mm \) |
| \( h \) = Weld Thickness | \( in \) | \( mm \) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
Perpendicular Force on PJP Fillet Weld formulas
|
||
|
\( \sigma \;=\; \dfrac{ P }{ L \cdot h \cdot ( t + h ) } \cdot \sqrt{ 2 \cdot H^2 + \dfrac{ ( t + h )^2 }{ 2 } } \) \( \tau \;=\; \dfrac{ 0.707 \cdot P }{ L \cdot h } \) |
||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Weld Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \tau \) (Greak symbol tau) = Shear Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( H \) = Height of Lever Arm | \( in \) | \( mm \) |
| \( L \) = Weld Length | \( in \) | \( mm \) |
| \( t \) = Plate Thickness | \( in \) | \( mm \) |
| \( P \) = Total Applied Force | \( lbf \) | \( N \) |
| \( h \) = Weld Penetration | \( in \) | \( mm \) |