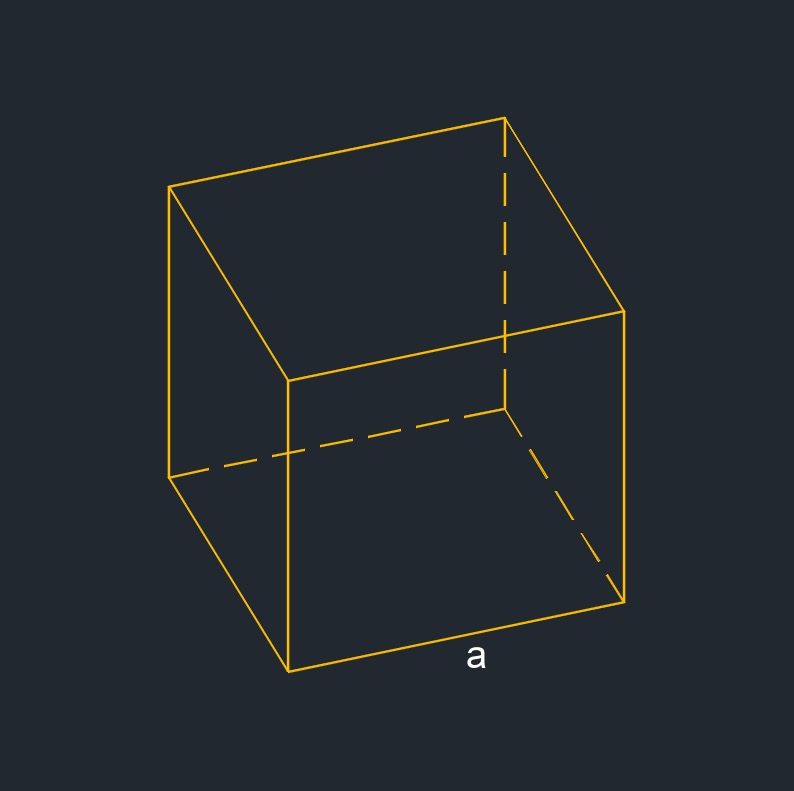
Cube
 Cube (a three-dimensional figure) is a regular polyhedron with square faces.
Cube (a three-dimensional figure) is a regular polyhedron with square faces.- All edges are the same length.
- All faces are squares
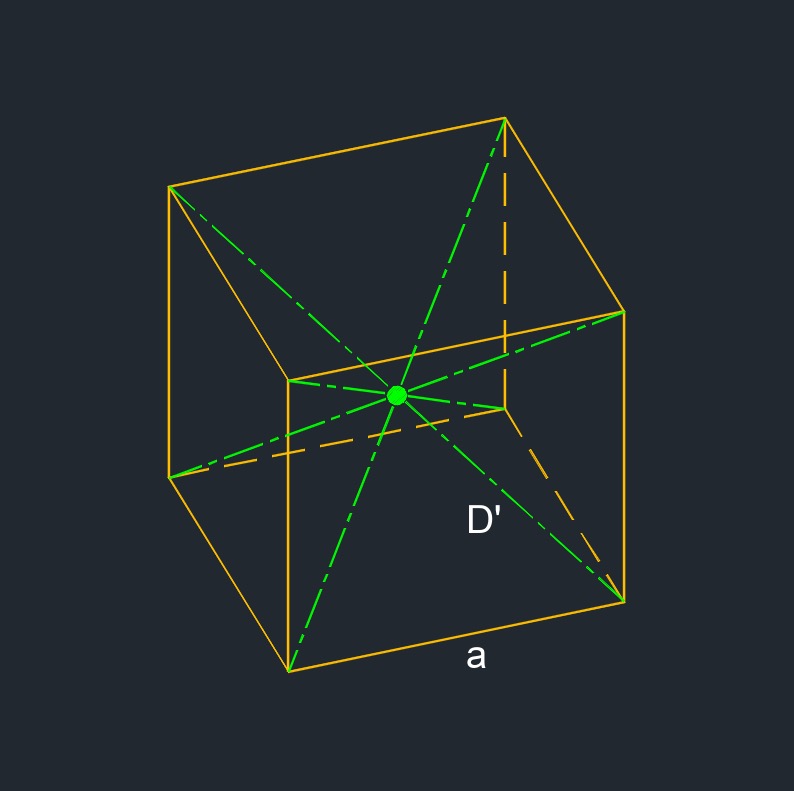
- Diagonal is a line from one vertices to another that is non adjacent.
- Circumscribed sphere is a polyhedron is a sphere that contains the polyhedron and touches each of the ployhedron's vertices.
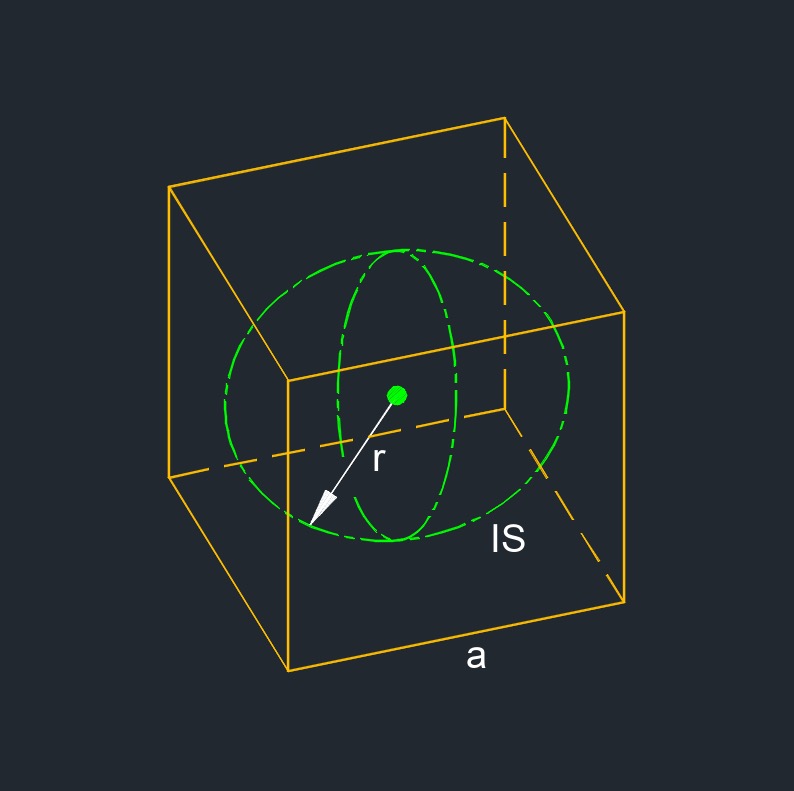
- Inscribed sphere is a convex polyhedron is a sphere that is contained within the polyhedron and tangent to each of the polyhedron's faces.
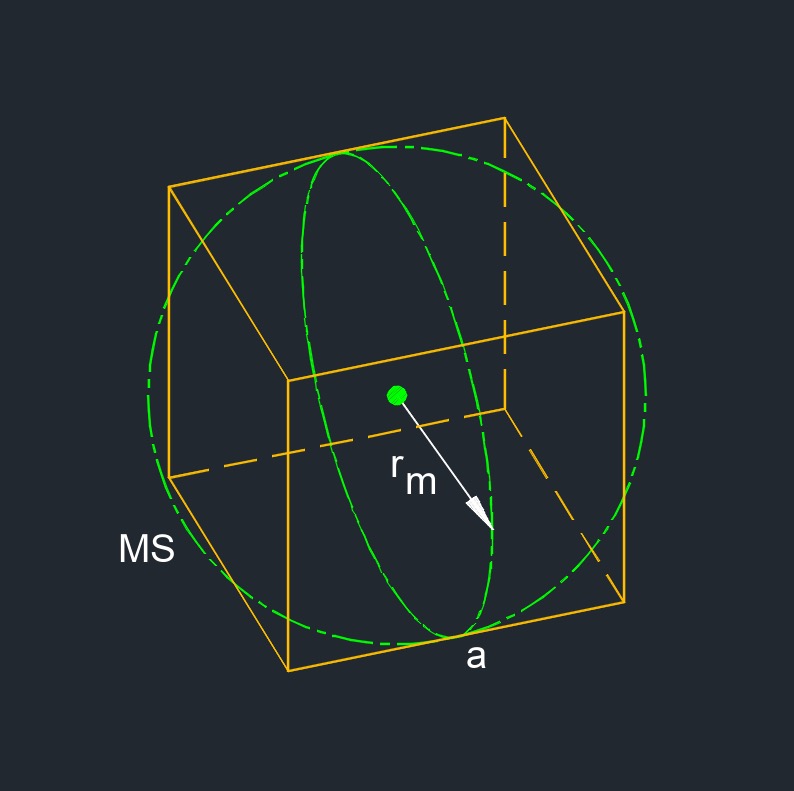
- Midsphere is a polyhedron is a sphere that is tangent to every edge of the polyhedron.
- 4 base diagonals
- 24 face diagonals
- 4 space diagonals
- 12 edges
- 6 faces
- 8 vertex
Cube Index
- Cube Circumscribed Sphere Radius
- Circumscribed Sphere Volume of a Cube
- Edge of a Cube
- Face Area of a Cube
- Inscribed Radius of a Cube
- Inscribed Sphere Volume of a Cube
- Midsphere Radius of a Cube
- Space Diagonal of a Cube
- Surface face Area of a Cube
- Volume of a Cube
- Weight of a Cube
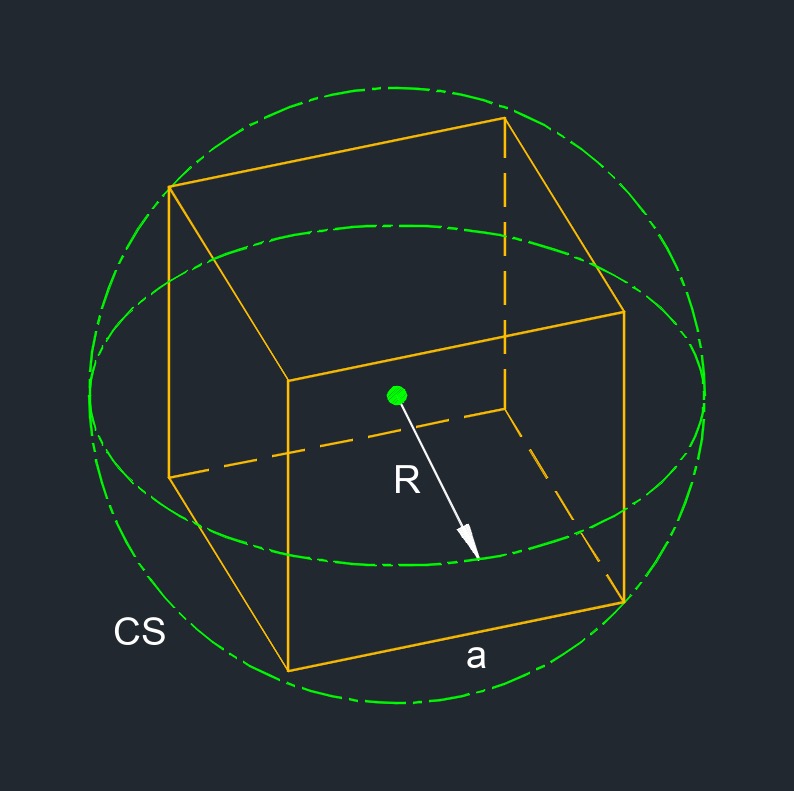
Cube Circumscribed Sphere Radius formulaCircumscribed sphere is a polyhedron is a sphere that contains the polyhedron and touches each of the ployhedron's vertices. |
||
| \( R = a \; \sqrt {3} \;/\;2 \) | ||
| Symbol | English | Metric |
| \( R \) = circumscribed sphere radius | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |

Circumscribed Sphere Volume of a Cube formulaCircumscribed sphere is a polyhedron is a sphere that contains the polyhedron and touches each of the ployhedron's vertices. |
||
| \( C_v = (3\;/\;4) \; \pi \; ( a\; \sqrt{3} \;/\;2 )^3 \) | ||
| Symbol | English | Metric |
| \( C_v \) = circumscribed sphere volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | |
Edge of a Cube formulas |
||
|
\( a = \sqrt{ A_s \;/\; 6 } \) \( a = V^{1/3} \) \( a = \sqrt{ 3 } \;\; (D' \;/\; 3) \) |
||
| Symbol | English | Metric |
| \( a \) = edge | \( in \) | \( mm \) |
| \( D' \) = space diagonal | \( in \) | \( mm \) |
| \( A_s \) = surface face area | \( in \) | \( mm \) |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
Face Area of a Cube formula |
||
| \( A_{area} = a^2 \) | ||
| Symbol | English | Metric |
| \( A_{area} \) = face area | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |
Inscribed Radius of a Cube formulaInscribed sphere is a convex polyhedron is a sphere that is contained within the polyhedron and tangent to each of the polyhedron's faces. |
||
| \( r = a\;/\;2 \) | ||
| Symbol | English | Metric |
| \( r \) = inside radius | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |
Inscribed Sphere Volume of a Cube formulaInscribed sphere is a convex polyhedron is a sphere that is contained within the polyhedron and tangent to each of the polyhedron's faces. |
||
| \( I_v = (3\;/\;4) \; \pi \; ( a \;/\;2 )^3 \) | ||
| Symbol | English | Metric |
| \( I_v \) = inscribed sphere volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | |
Midsphere Radius of a Cube formulaMidsphere is a polyhedron is a sphere that is tangent to every edge of the polyhedron. |
||
| \( r_m = (a\;/\;2)\; \sqrt {2} \) | ||
| Symbol | English | Metric |
| \( r_m \) = midsphere radius | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |
Space Diagonal of a Cube formula |
||
| \( D' = \sqrt {3} \;a \) | ||
| Symbol | English | Metric |
| \( D' \) = space diagonal | \( in \) | \( mm \) |
| \( a \) = edge | \( in \) | \( mm \) |
Surface face Area of a Cube formula |
||
| \( A_s = 6\;a^2 \) | ||
| Symbol | English | Metric |
| \( A_s \) = surface face area | \( in^2 \) | \( mm^2 \) |
| \( a \) = edge | \( in \) | \( mm \) |

Surface to volume ratio of a Cube formula |
||
| \( S_v = 6\;/\;a \) | ||
| Symbol | English | Metric |
| \( S_v \) = surface to volume ratio | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |

Volume of a Cube formula |
||
| \( V = a^3 \) | ||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = edge | \( in \) | \( mm \) |

Weight of a Cube formula |
||
| \( m = a^3 \; \rho \) | ||
| Symbol | English | Metric |
| \( m \) = mass | \( lbm \) | \( kg \) |
| \( \rho \) (Greek symbol rho) = density | \(lbm\;/\;ft^3\) | \(kg\;/\;m^3\) |
| \( a \) = edge | \( in \) | \( mm \) |

Tags: Volume Solid Prism