Rotational Stiffness

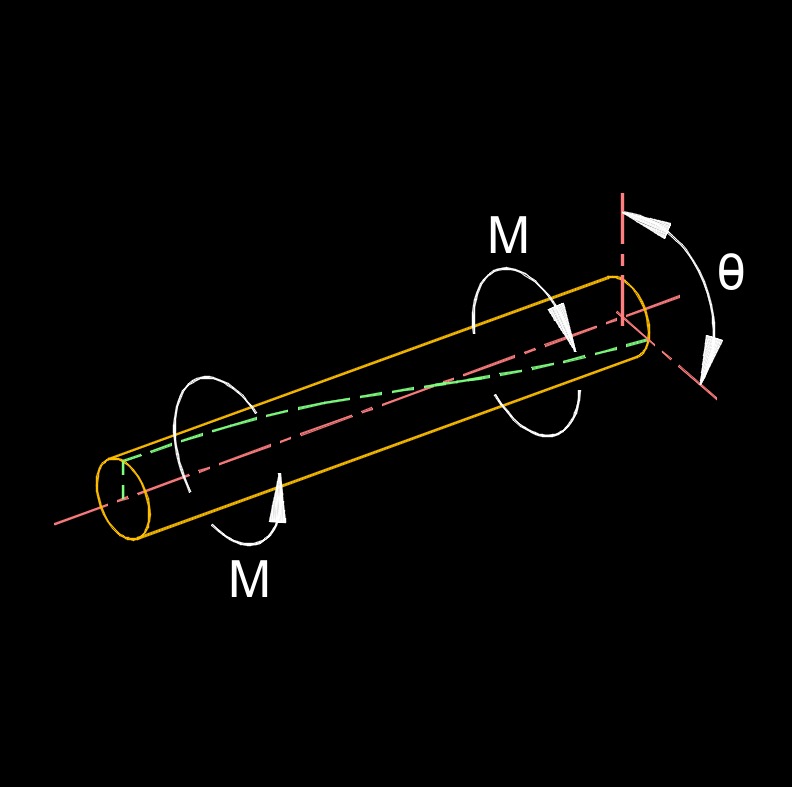Rotational stiffness, abbtrviated as k, also called rotational rigidity or torsional stiffness, is used in structural engineering and mechanics to describe the resistance of an object or structure to undergo rotational deformation when subjected to a torque or moment.  In structural systems, such as beams, columns, or shafts, rotational stiffness is crucial to understanding their behavior under applied loads.  It is analogous to linear stiffness, which describes how much an object resists linear deformation under axial loads.

For example, consider a simple beam supported at both ends.  When a moment is applied to one end of the beam, it tends to rotate about its longitudinal axis.  The rotational stiffness of the beam determines how much it will resist this rotational deformation.  A structure with higher rotational stiffness will experience less rotation under the same applied torque compared to a structure with lower rotational stiffness.

The formula for rotational stiffness can be derived from Hooke's law for torsion, and it is usually defined based on the geometry and material properties of the structure.  In more complex structural analysis, rotational stiffness is an essential parameter used to model the behavior of elements like beams, columns, and connections in finite element analysis and other numerical methods.

 

Rotational Stiffness formula
\( k \;=\; M\;/\;\theta  \)     (Rotational Stiffness) \( M \;=\; k \; \theta  \)  \( \theta \;=\; M\;/\;k \)
Symbol	English	Metric
\( k \) = Rotational Stiffness	\(lbm-ft\;/\;deg\)	\(kg-m\;/\;rad\)
\( M \) = Applied Moment	\(lbm-ft\;/\;sec\)	\(kg-m\;/\;s\)
\( \theta \)  (Greek symbol theta) = Angle of the Rotation	\(deg\)	\(rad\)