Angular Deflection Length
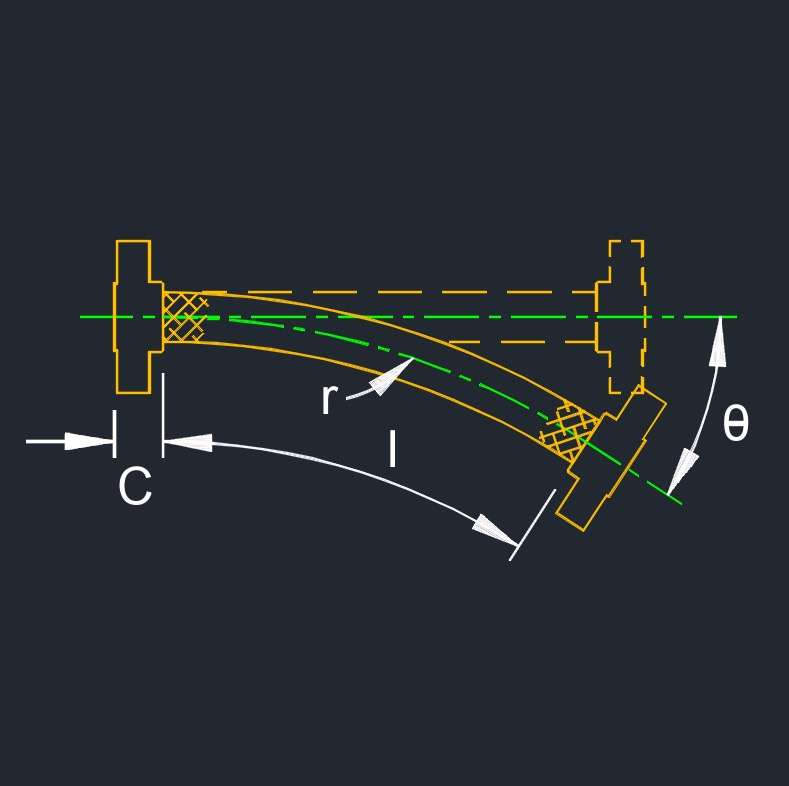 Angular deflection length is the amount of rotational movement or deflection that a structural element or connection can tolerate before it reaches a critical point of failure or instability. This concept is commonly encountered in engineering and construction, particularly in the design of structures and connections that are subjected to various loads and forces. In structural engineering, elements like beams, columns, pipe, and joints can experience angular deflection under the influence of external forces such as loads, moments, and torsion. The angular deflection length is the distance along the element at which a certain angle of rotation or deflection occurs due to these forces.
Angular deflection length is the amount of rotational movement or deflection that a structural element or connection can tolerate before it reaches a critical point of failure or instability. This concept is commonly encountered in engineering and construction, particularly in the design of structures and connections that are subjected to various loads and forces. In structural engineering, elements like beams, columns, pipe, and joints can experience angular deflection under the influence of external forces such as loads, moments, and torsion. The angular deflection length is the distance along the element at which a certain angle of rotation or deflection occurs due to these forces.
Angular deflection length is important to determine the stability and integrity of a structure. Engineers use calculations and analysis to ensure that the angular deflections experienced by structural elements remain within safe limits. Excessive angular deflection can lead to structural failure, reduced functionality, or compromised safety.
Factors that affect angular deflection length include the type of material, the geometry of the element, the magnitude and direction of applied loads, and the support conditions. Design standards and codes provide guidelines to ensure that structures are designed with acceptable levels of angular deflection to maintain stability and safety.
Angular Deflection Length Formula |
||
|
\( l \;=\; \dfrac{ \pi \cdot r \cdot \theta }{ 180 }\) (Angular Deflection Length) \( r \;=\; \dfrac{ l \cdot 180 }{ \pi \cdot \theta }\) \( \theta \;=\; \dfrac{ l \cdot 180 }{ \pi \cdot r }\) |
||
| Symbol | English | Metric |
| \( l \) = length of beam or hose | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = centerline bend radius | \( in \) | \( mm \) |
| \( \theta \) (Greek symbol theta) = angular deflection | \( in \) | \( mm \) |

