Torsion

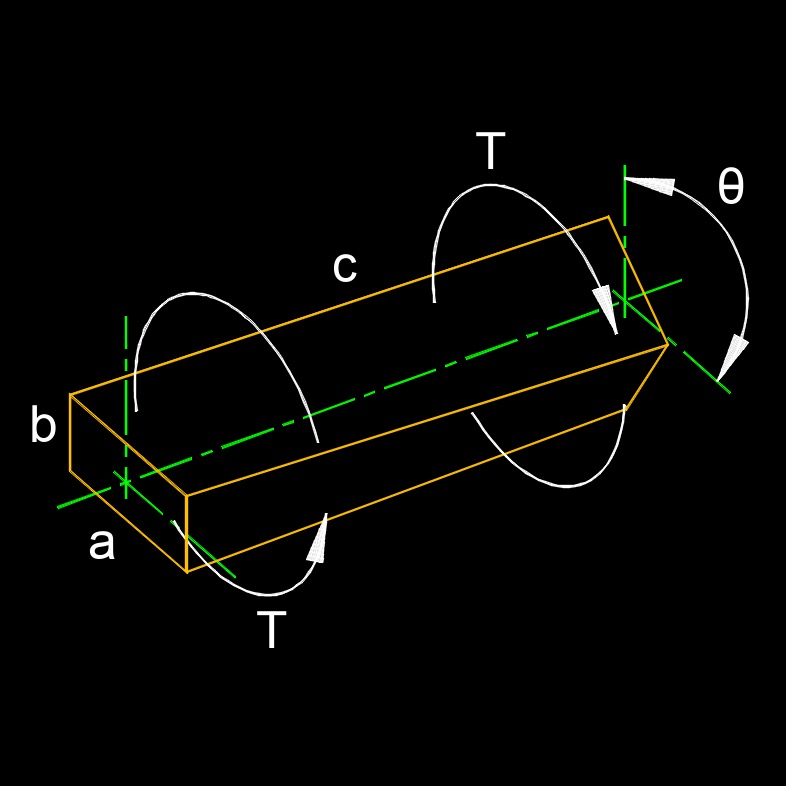
Torsion, abbreviated as T, also called torsion force or twist force, refers to the twisting or rotational deformation of an object when subjected to a torque or twisting force.  This force causes the object to twist about its longitudinal axis.  It is the stress of twisting of an object due to applied torque between both ends of an object.  In sections perpendicular to the torque axis, the shear stress in this section is perpendicular to the radius.  Torsion is a fundamental concept in mechanics and is often encountered in various engineering and physics applications.

Key Points about torsion

• Torque  -  Torsion is induced by the application of torque, which is a force that tends to rotate an object around its axis.  Torque is typically measured in units like Newton-meters (N·m) or foot-pounds (ft·lb).
• Torsional Stress  -  Torsion leads to the development of internal stresses within the material of the object.  These stresses are referred to as torsional or shear stresses and are responsible for the deformation and potential failure of the material.
• Torsional Deformation  -  When a torsional force is applied to an object, it undergoes a deformation characterized by angular displacement.  The amount of deformation depends on various factors, including the magnitude of the torque, the geometry of the object, and the material properties.
• Torsional Springs  -  Torsion is also the principle behind torsional springs or torsion bars, which are used in various mechanical systems to store and release energy through twisting deformation.  These are commonly found in applications like automotive suspensions.
• Engineering Applications  -  Torsion is a critical consideration in the design and analysis of mechanical components such as shafts, gears, and other rotating parts.  Engineers need to calculate and design for torsional stresses to ensure the safety and performance of these components.
• Torsion in Materials Testing  -  Torsion tests are often performed in material testing to determine the shear modulus or modulus of rigidity, which describes a material's resistance to shear deformation.

 

Torsion FORMULA
\( T \;=\; J \; \tau \;/\; \rho \)     (Torsion) \( J \;=\; T \; \rho \;/\; \tau \) \( \tau \;=\; T \; \rho \;/\; J \) \( \rho \;=\; J \; \tau \;/\; T \)
Symbol	English	Metric
\( T \) = Applied Torque or Moment of Torsion	\(lbf-ft\)	\(N-m\)
\( J \) = Torsion Constant (Polar Momentum of Inertia)	\(in^4\)	\(mm^4\)
\( \tau \) (Greek symbol tau) = Maximum Shear Stress at the Outer Surface	\(lbf\;/\;in^2\)	\(Pa\)
\( \rho \)  (Greek symbol rho) = Distance Between the Rotational Axis and the Farthest Point in the Section	\(in\)	\(mm\)