Angular Deflection
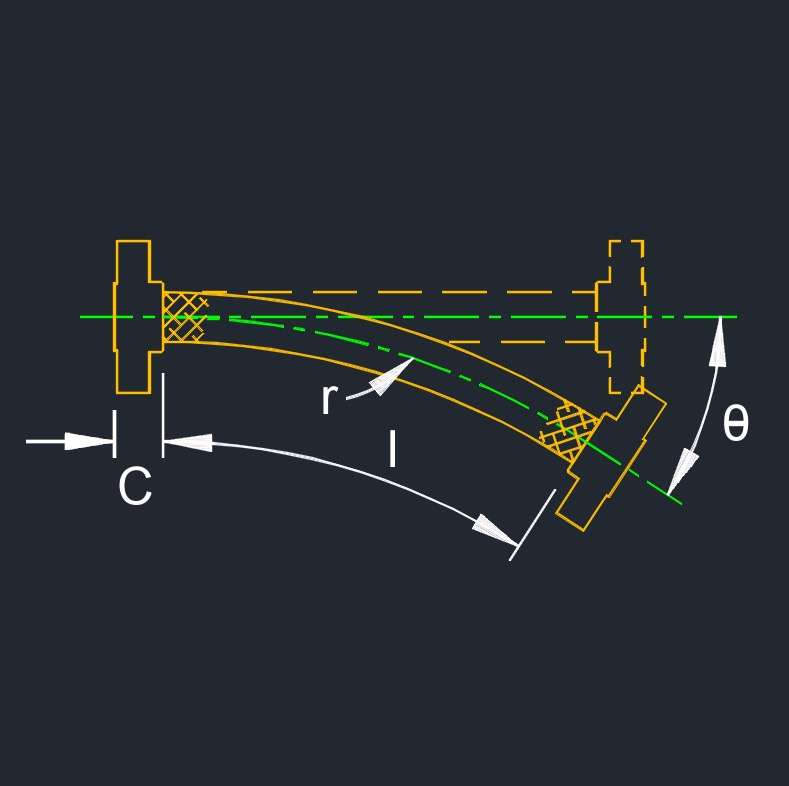Angular deflection, abbreviated as \( \theta \) (Greek symbol theta), is when a flex connector is bent on it's centerline. One end of the hose assembly is deflected or bent with the other end remaining parallel.
Angular deflection also refers to the change in the angle or displacement of an object or structure from its original position due to the application of an external force or moment. It measures the rotation or bending experienced by the object under the influence of an applied load.
Angular deflection can occur in various scenarios and structures. For example, in a beam subjected to bending, the angular deflection represents the change in the angle between two points along the beam's neutral axis. The magnitude of angular deflection depends on factors such as the applied load, the geometry of the structure, and the material properties.
Angular deflection is an important parameter in engineering and design, as it affects the performance, strength, and stability of structures. Engineers use angular deflection analysis to ensure that a structure or component remains within acceptable limits to avoid failure, excessive deformation, or unwanted movement. In some cases, angular deflection may need to be limited or controlled to meet specific design requirements or operational constraints. Various design strategies, such as adding supports, using stiffer materials, or altering the geometry, can be employed to reduce angular deflection and ensure the desired performance of the structure.
Angular Deflection formula |
||
|
\( \theta = F \;l \;/\; 2\; \lambda\; I \) (Angular Deflection) \( F = \theta \; 2 \; \lambda \; I \;/\; l \) \( l = \theta \; 2 \; \lambda \; I \;/\; F \) \( \lambda = F \; l \;/\; \theta \; 2 \; I \) \( I = F \; l \;/\; \theta \; 2 \; \lambda \) |
||
| Symbol | English | Metric |
| \( \theta \) (Greek symbol theta) = Angular Deflection | \( deg \) | \( rad \) |
| \( F \) = Force Acting on the Tip of Beam or Hose | \( lbf \) | \( N \) |
| \( l \) = Beam or Hose Length | \( in \) | \( mm \) |
| \( \lambda \) (Greek symbol lambda) = Elastic Modulus | \(lbf \;/\; in^2\) | \(Pa\) |
| \( I \) = Area Moment of Inertia | \( in^4 \) | \( mm^4 \) |
Tags: Force Deflection Flex Connector