Loss Coefficient

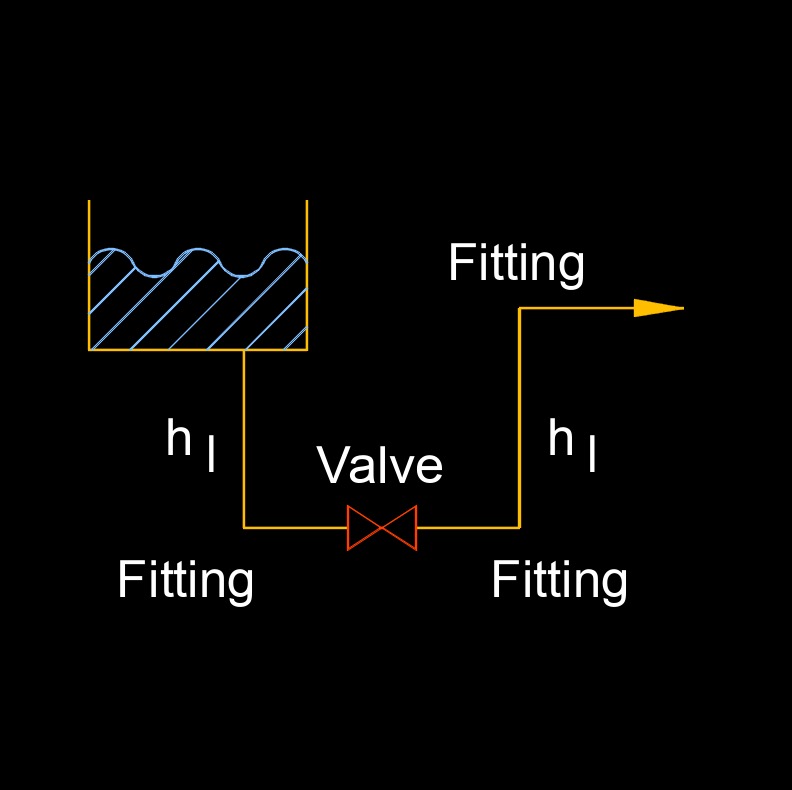Loss coefficient, abbrevated as K, a dimensionless number, also called head loss coefficient or flow resistance coefficient, measures the minor loss to the change in velocity due to friction thru pipes, fittings, and valves.  Most piping consists of more than just straight lines, these losses are termed a minor loss.  Any bend or tee, expansion or contraction, valve opening or partially closing can cause minor or even major losses.

When fluid flows through pipes, valves, fittings, or other flow elements, friction and other factors result in a loss of energy.  The loss coefficient is a measure of the efficiency or effectiveness of the component in maintaining fluid energy.  It represents the ratio of the energy loss or pressure drop across the component to the dynamic pressure of the flowing fluid.  The loss coefficient can vary depending on the geometry, roughness, and flow conditions of the component.  It is determined experimentally through tests or obtained from empirical correlations specific to different types of flow elements.

The value of the loss coefficient is influenced by various factors, including the Reynolds number, flow velocity, fluid properties, and geometric characteristics of the component.  It is important to note that the loss coefficient is often specific to a particular flow regime and needs to be carefully selected or calculated based on the specific conditions and application.

The loss coefficient is used in various equations and formulas, such as the Darcy-Weisbach equation or the Hazen-Williams equation, to estimate pressure drops, flow rates, and the overall performance of a flow system.  It allows engineers to analyze and predict the behavior of fluid flow, optimize system designs, and evaluate the efficiency of components in terms of energy loss.  The loss coefficient values for different flow elements are available in published standards, handbooks, and engineering references, providing guidance for engineers and designers in fluid flow calculations and system analysis.

 

Loss Coefficient formula
\( K \;=\; h_l \;  2 \; g \;/\; v^2   \)     (Loss Coefficient) \( h_l \;=\; K \;  v^2  \;/\; 2 \; g   \) \( v \;=\; \sqrt{ 2 \; g  \; ( K  \;/\; h_l )  }  \)
Symbol	English	Metric
\( K \) = Loss Coefficient	\( dimensionless \)	\( dimensionless \)
\( h_l \) = Head Loss	\( ft \)	\( m \)
\( g \) = Gravitational Acceleration	\(ft \;/\; sec^2\)	\(m \;/\; s^2\)
\( v \) = Flow Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)

 

Loss Coefficient
Component	Loss Coefficient \(K\)
Elbows
90 Short Elbow, flanged	0.3
90 Short Elbow, threaded	1.5
90 Long Elbow, flanged	0.2
90 Long Elbow, threaded	0.7
45 Long Elbow, flanged	0.2
45 Short Elbow, threaded	0.4
180 Return
180 Return, flanged	0.2
180 Return, threaded	1.5
Tees
Line flow, flanged	0.2
Line flow, threaded	0.9
Branch flow, flanged	1.0
Branch flow, threaded	2.0
Union, threaded	0.08
Valves
Diaphragm, fully open	2.3
Diaphragm, 1/4 closed	21
Diaphragm, 1/2 closed	4.3
Globe, fully open	10
Angle, fully open	2
Gate, fully open	0.15
Gate, 1/4 closed	0.26
Gate, 1/2 closed	2.1
Gate, 3/4 closed	17
Swing Check, forward flow	2
Swing Check, backward flow	\(\infty\)
Ball, fully open	0.05
Ball, 1/3 closed	5.5
Ball, 2/3 closed	210
Water meter	7