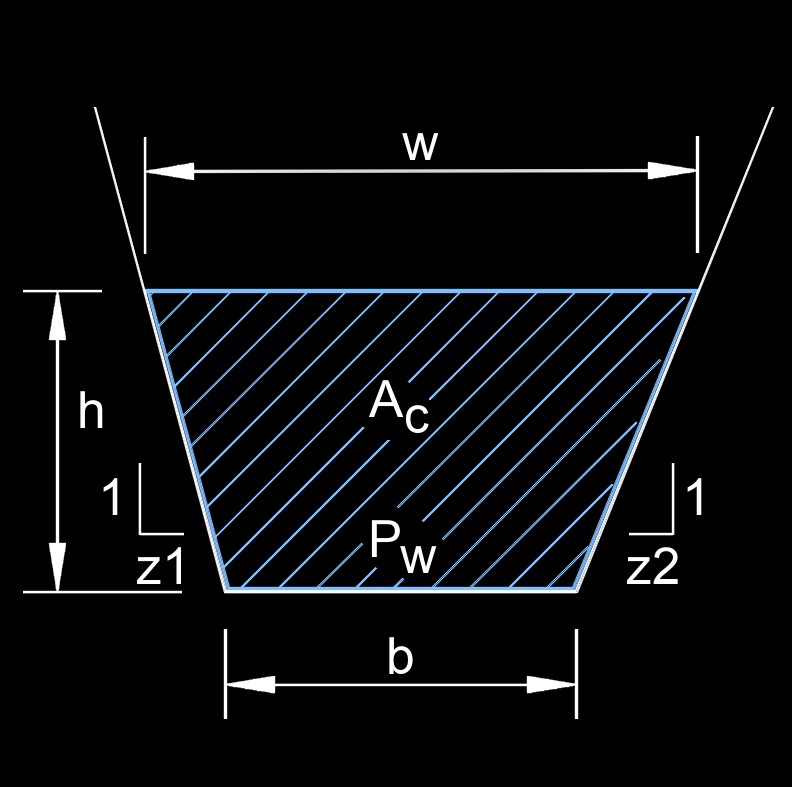
Hydraulic Radius of a Trapezoidal Channel (Unequal Side Slopes) Formula |
||
| \( r_h \;=\; \dfrac{ \dfrac{h}{2} \cdot ( b + w ) }{ b + h \cdot ( \sqrt { 1 + z_{1}{^2} } + \sqrt{ 1 + z_{2}{^2} } \;) }\) | ||
| Symbol | English | Metric |
| \( r_h \) = hydraulic radius | \(ft\) | \(m\) |
| \( A_c \) = area cross-section of flow | \(ft^2\) | \(m^2\) |
| \( b \) = bottom width of fluid | \(ft\) | \(m\) |
| \( h \) = depth of fluid | \(ft\) | \(m\) |
| \( g \) = gravitational acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
| \( w \) = top width of fluid | \(ft\) | \(m\) |
| \( P_w \) = wetting perimeter | \(ft\) | \(m\) |
| \( z_1 \) = width of channel slope | \(ft\) | \(m\) |
| \( z_2 \) = width of channel slope | \(ft\) | \(m\) |
Hydraulic radius, abbreviated as \(r_h\), is the area cross-section of water in a pipe or channel divided by the wetting perimeter.
