Centripetal Force

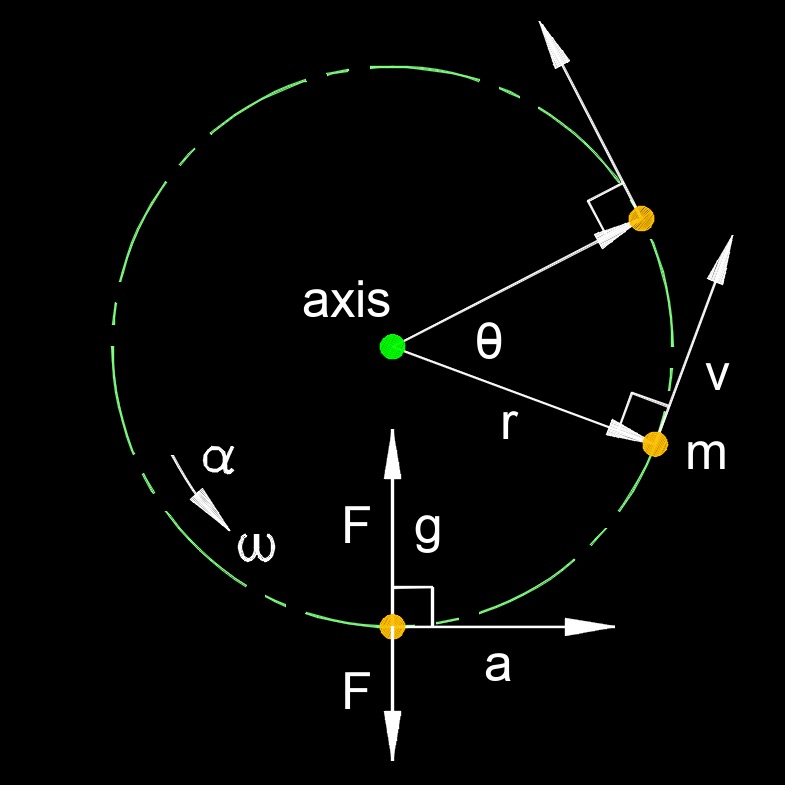Centripetal force, abbreviated as \( F_c \) or \( F_{cp} \), is the force that makes an object follow a curved path.  It is a force generated when an object keeps traveling along a axis of rotation.  An example of of centripetal force is when driving around a corner.  The centripetal force is the reactionary force equal to the centrifugal force felt.  When centripetal force is greater than the centrifugal force, the vehicle will lose traction and slide.

The most common example of centripetal force is when a body moves with uniform speed along a circular path.  The centripetal force is directed at right angles to the motion and points to the center or the curve.   The equations below and their associated calculator shows two different ways of calculating centripetal force.

 

centripetal force formula
\( F_c =  m \; a_c \)     (Centripetal Force) \( m =  F_c\;/\;a_c \)  \( a_c =  F_c\;/\;m \)
Symbol	English	Metric
\( F_c \) = Centripetal Force	\(lbf\)	\(N\)
\( a_c \) = Centripetal Acceleration	\(ft\;/\;sec^2\)	\(m\;/\;s^2\)
\( m \) = Mass	\(lbm\)	\(kg\)

 

centripetal force formula
\( F_c =  m \; v^2 \;/\; r \)
Symbol	English	Metric
\( F_c \) = Centripetal Force	\(lbf\)	\(N\)
\( m \) = Mass	\(lbm\)	\(kg\)
\( r \) = Radius of Circular Path	\(ft\)	\(m\)
\( v \) = Velocity	\(ft\;/\;sec\)	\(m\;/\;sec\)

 

centripetal force formula
\( F_c =  m \; \omega^2 \; r  \)
Symbol	English	Metric
\( F_c \) = Centripetal Force	\(lbf\)	\(N\)
\( \omega \)   (Greek symbol omega) = Angular Velocity	\(deg\;/\;sec\)	\(rad\;/\;s\)
\( m \) = Mass	\(lbm\)	\(kg\)
\( r \) = Radius of Circular Path	\(ft\)	\(m\)