Initial Velocity Formula |
||
|
\( v_i \;=\; v_f - a \cdot t \) (Initial Velocity) \( v_f \;=\; v_i + a \cdot t \) \( a \;=\; \dfrac{ v_f - v_i }{ t } \) \( t \;=\; \dfrac{ v_f - v_i }{ a } \) |
||
| Symbol | English | Metric |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( v_f \) = final velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( a \) = acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
| \( t \) = time | \( sec \) | \( s \) |
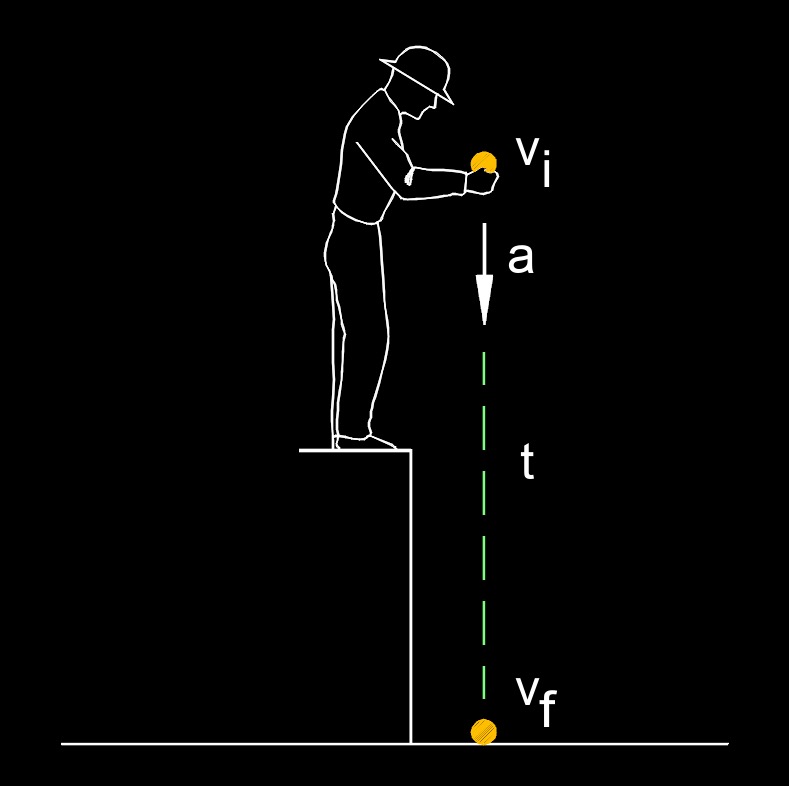Initial velocity, abbreviated as \( v_i \), is the velocity an object has at the very start of a motion or event being observed. It represents both the speed and direction of the object at time, before any forces, accelerations, or changes in motion have occurred. In physics problems, the initial velocity serves as a starting condition for calculating future position, velocity, or energy. Knowing the initial velocity allows you to determine how an object’s movement will evolve over time when combined with acceleration, forces, or external influences.
Initial Velocity Formula |
||
|
\( v_i \;=\; \dfrac{ s }{ t } - ( \dfrac{1}{2} \cdot a \cdot t )\) (Initial Velocity) \( s \;=\; t \cdot v_i + \left( \dfrac{1}{2} \cdot a \cdot t^2 \right) \) \( t \;=\; \dfrac{ - v_i \pm \sqrt{ v_i^2 + 2 \cdot a \cdot s } }{ a } \) \( a \;=\; \dfrac{ 2 \cdot s }{ t^2 } - \dfrac{ 2 \cdot v_i }{ t } \) |
||
| Symbol | English | Metric |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( s \) = displacement | \( ft \) | \( m \) |
| \( t \) = time | \( sec \) | \( s \) |
| \( a \) = acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
Initial Velocity Formula |
||
|
\( v_i \;=\; \sqrt{ v_f - ( 2 \cdot a \cdot d ) } \) (Initial Velocity) \( v_f \;=\; v_i^2 + ( 2 \cdot a \cdot d ) \) \( a \;=\; \dfrac{ v_f - v_i^2 }{ 2 \cdot d } \) \( d \;=\; \dfrac{ v_f - v_i^2 }{ 2 \cdot a } \) |
||
| Symbol | English | Metric |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( v_f \) = final velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( a \) = acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
| \( d \) = distance | \(ft\) | \(m\) |