- See Article - Beam Design Formula
Cantilever Beam - Concentrated Load at Any Point formulas |
||
|
\( R = V \;=\; P \) \( M_{max} \; (at\; fixed\; end ) \;=\; P\cdot b \) \( M_x \; (when \; x > a ) \;=\; P \cdot ( x - a ) \) \( \Delta_{max} \; (at\; fixed\; end ) \;=\; \dfrac{ P\cdot b^2 }{ 6\cdot \lambda \cdot I } \cdot ( 3\cdot L - b ) \) \( \Delta_a \; (at \;point\; of \;load ) \;=\; \dfrac{ P\cdot b^3 }{ 3 \cdot \lambda\cdot I }\) \( \Delta_x \; (when \; x < a ) \;=\; \dfrac{ P\cdot b^2 }{ 6\cdot \lambda\cdot I } \cdot ( 3\cdot L - 3\cdot x - b ) \) \( \Delta_x \; (when \; x > a ) \;=\; \dfrac{ P\cdot ( L - x )^2 }{ 6 \cdot \lambda\cdot I } \cdot ( 3\cdot b - L + x ) \) |
||
| Symbol | English | Metric |
| \( \Delta \) = deflection or deformation | \(in\) | \(mm\) |
| \( x \) = horizontal distance from reaction to point on beam | \(in\) | \(mm\) |
| \( M \) = maximum bending moment | \(lbf-in\) | \(N-mm\) |
| \( V \) = maximum shear force | \(lbf\) | \(N\) |
| \( \lambda \) (Greek symbol lambda) = modulus of elasticity | \(lbf\;/\;in^2\) | \(Pa\) |
| \( R \) = reaction load at bearing point | \(lbf\) | \(N\) |
| \( I \) = second moment of area (moment of inertia) | \(in^4\) | \(mm^4\) |
| \( L \) = span length of the bending member | \(in\) | \(mm\) |
| \( P \) = total concentrated load | \(lbf\) | \(N\) |
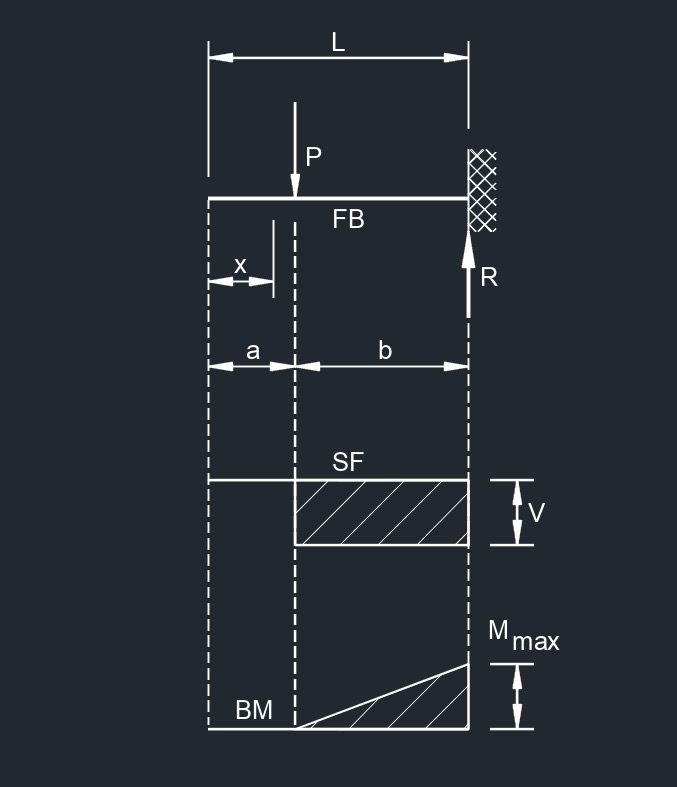
Diagram Symbols
Bending moment diagram (BMD) - Used to determine the bending moment at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Free body diagram (FBD) - Used to visualize the applied forces, moments, and resulting reactions on a structure in a given condition.
Shear force diagram (SFD) - Used to determine the shear force at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Uniformly distributed load (UDL) - A load that is distributed evenly across the entire length of the support area.
