Beam Design Formulas

Structural beam design refers to the process of determining the appropriate size and shape of beams that will be used in construction to support and distribute loads within a building or structure.  Beams are horizontal or inclined structural members that carry vertical loads.  The design of structural beams involves several important considerations to ensure the safety, stability, and efficiency of a structure.

• See Article  -  Beam Design Formulas, Frame Design Formulas, Plate Design Formulas, Geometric Properties of Structural Shapes, Welding Stress and Strain Connections, and Welding Symbols

Key Points about Design of Structural Beams

Diagram Symbols

Simple Supported Beam

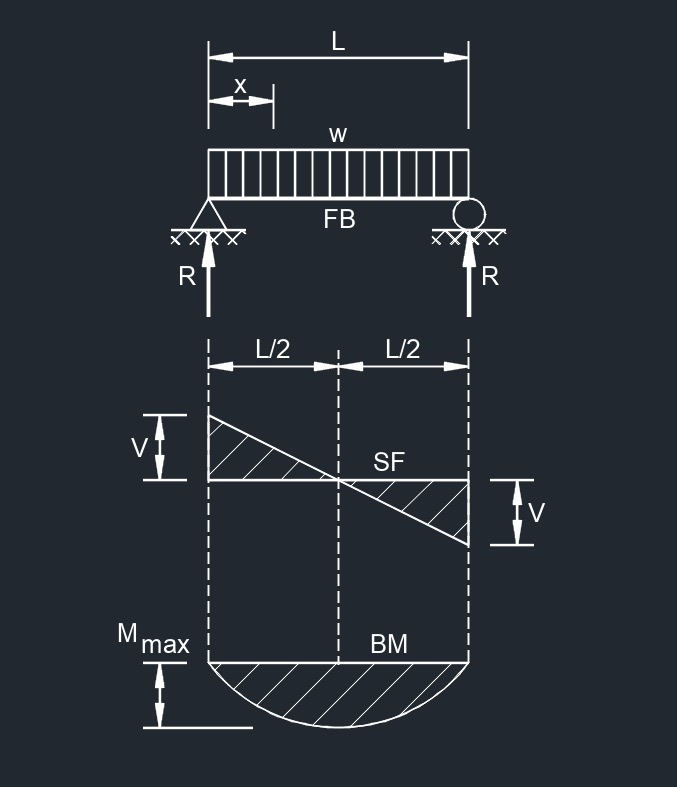Uniformly Distributed Load 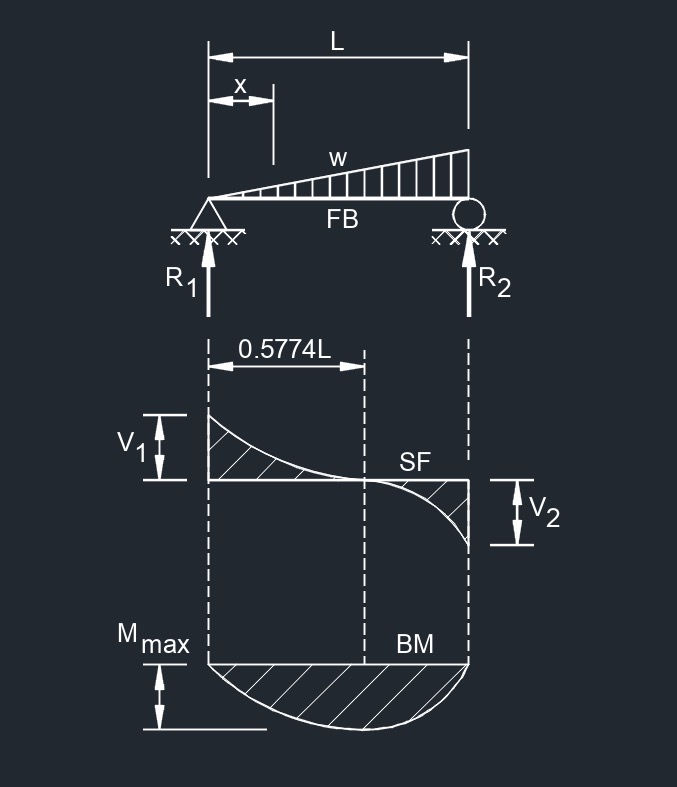Load Increasing Uniformly to One End 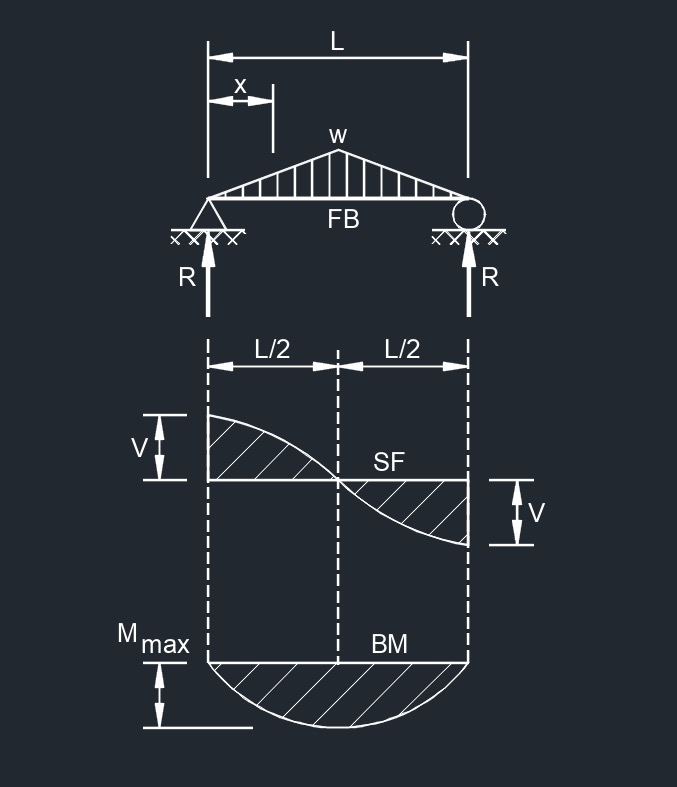Load Increasing Uniformly to Center 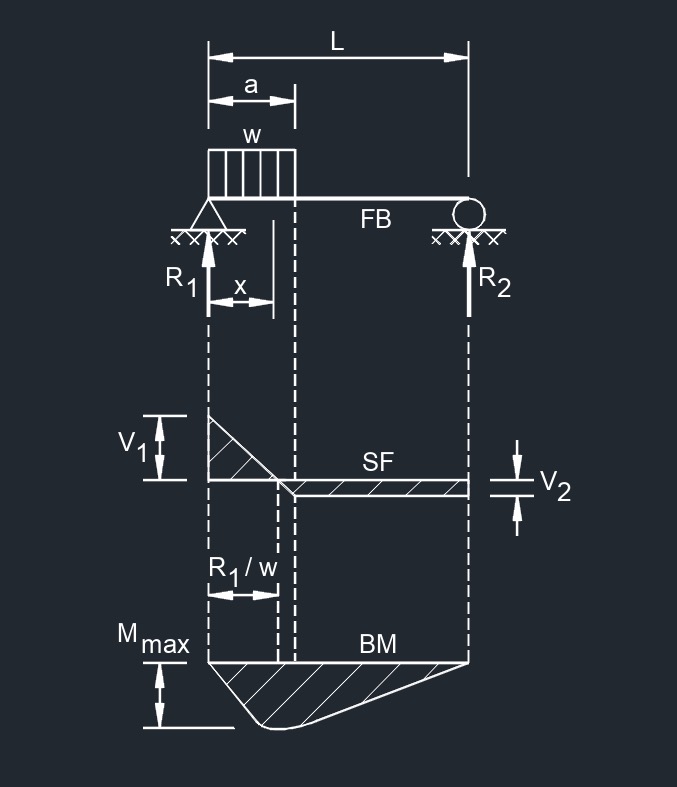Uniform Load Partially Distributed at One End

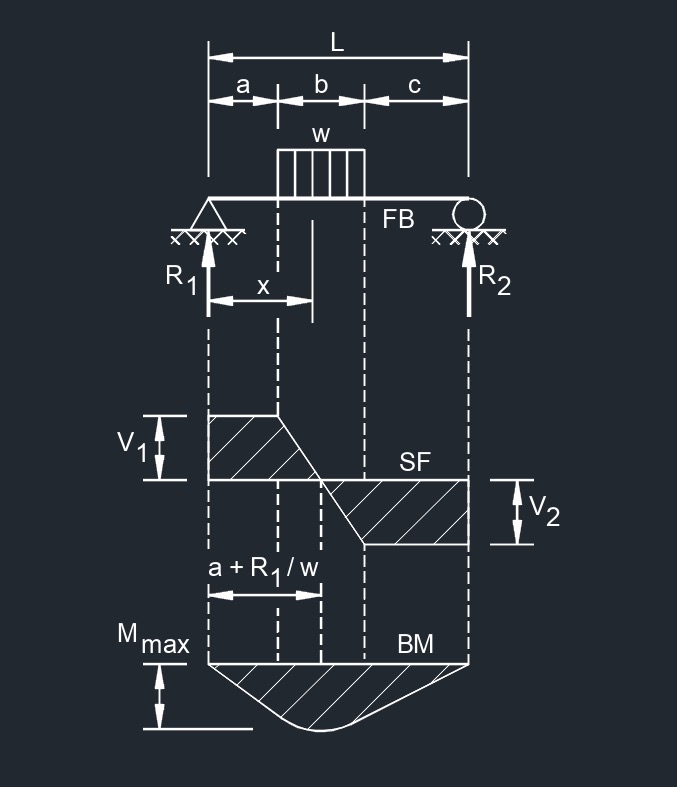Uniform Load Partially Distributed at Any Point 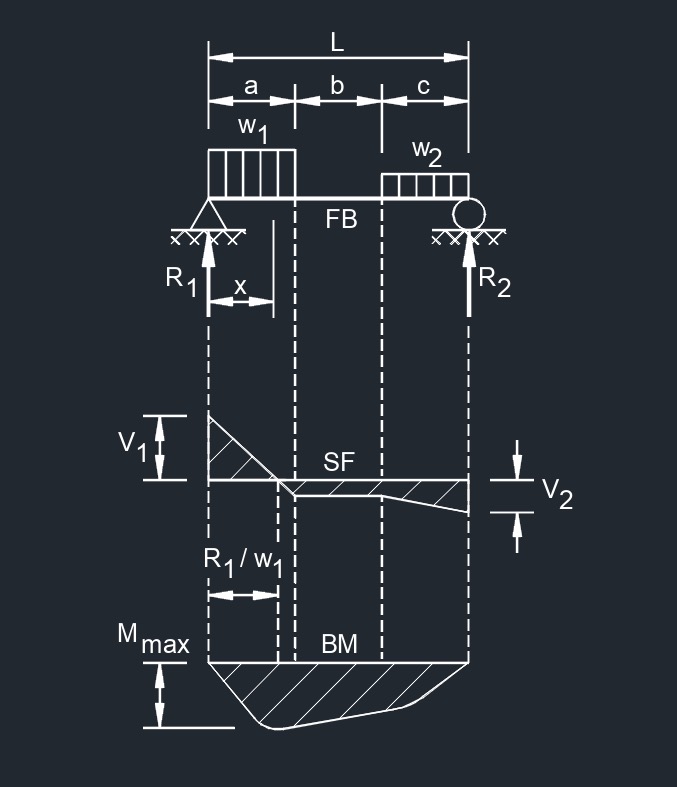Uniform Load Partially Distributed at Each End 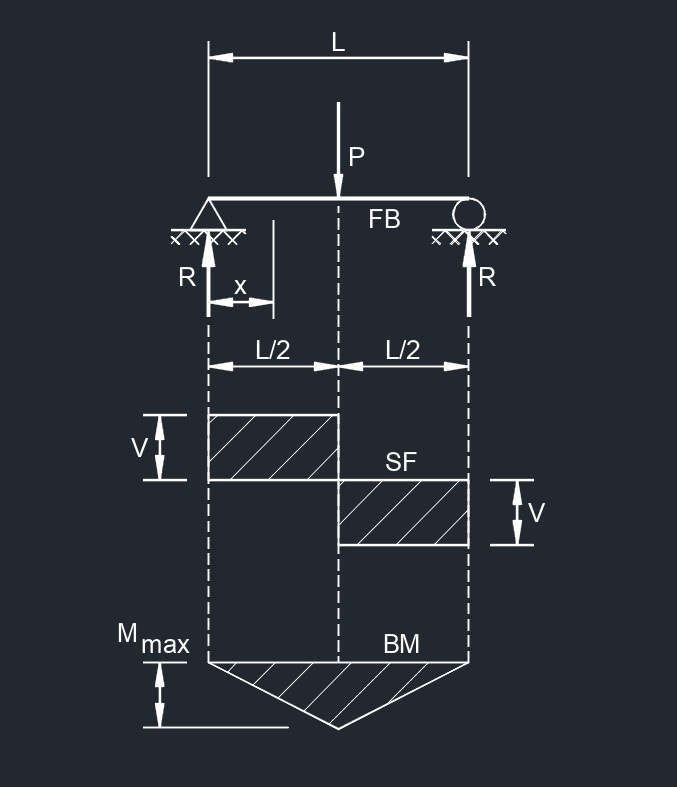Concentrated Load at Center 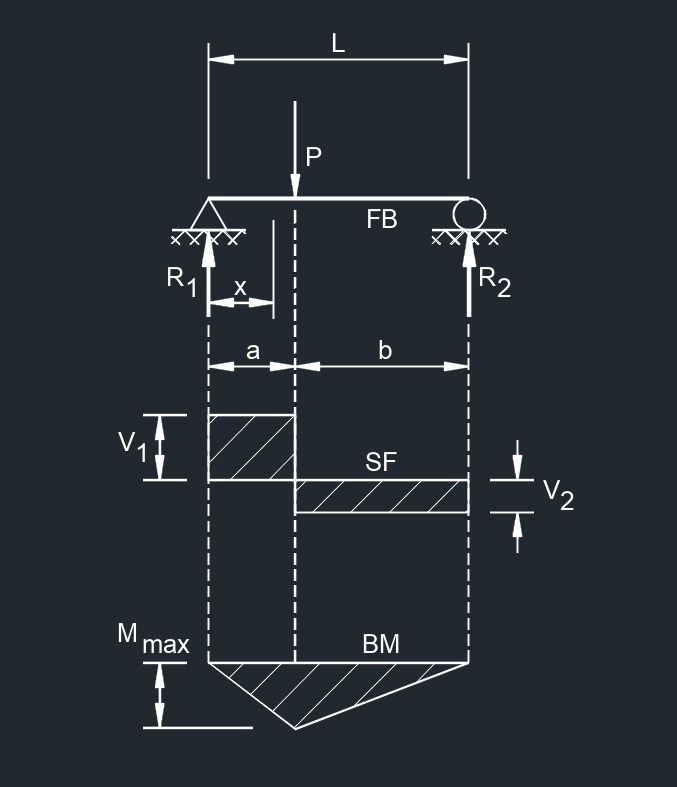Concentrated Load at Any Point

 

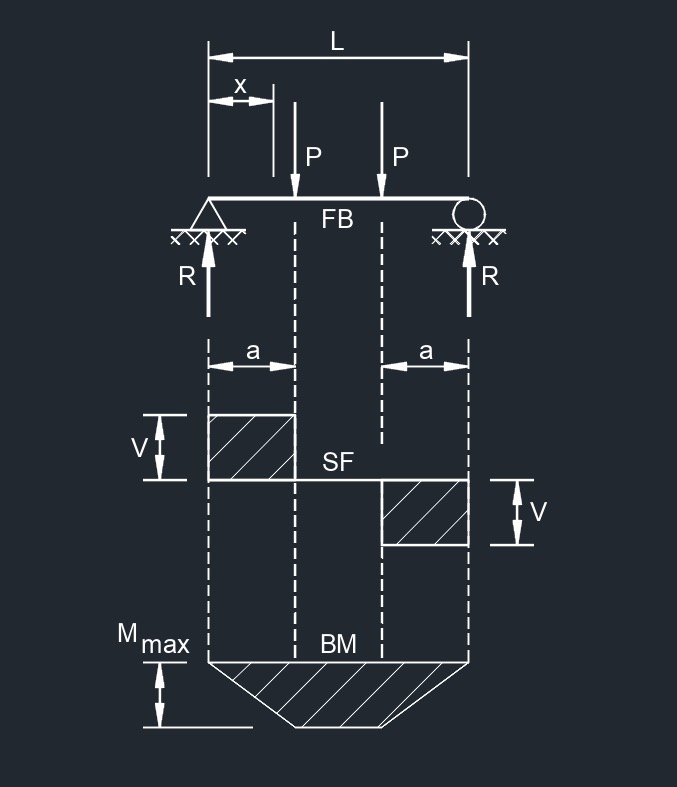Two Point Loads Equally Spaced 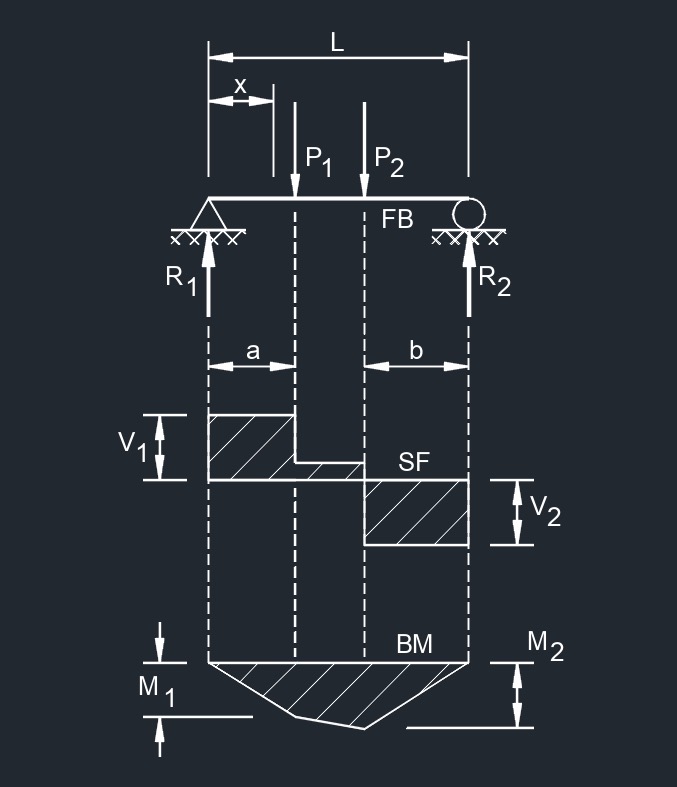Two Equal Point Loads Unequally Spaced 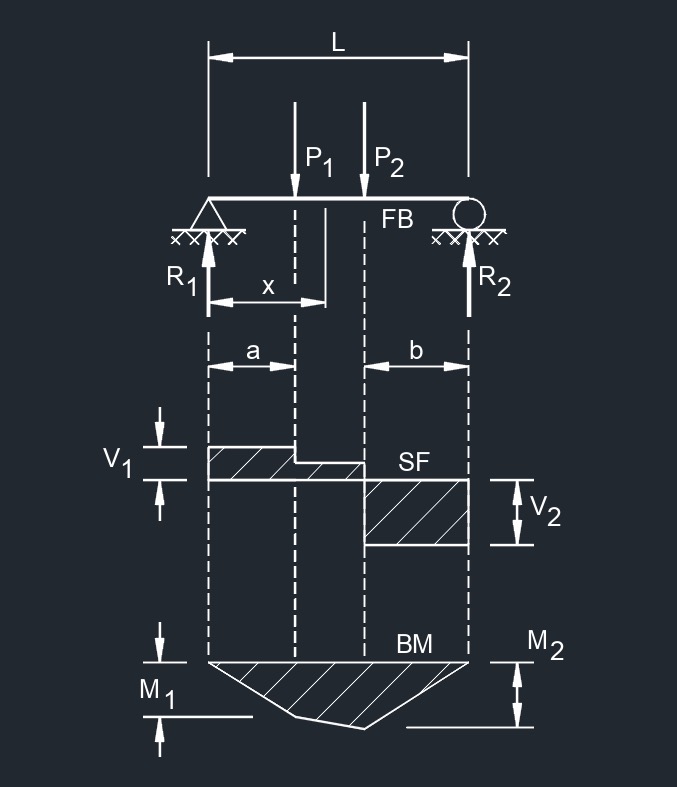Two Unequal Point Loads Unequally Spaced 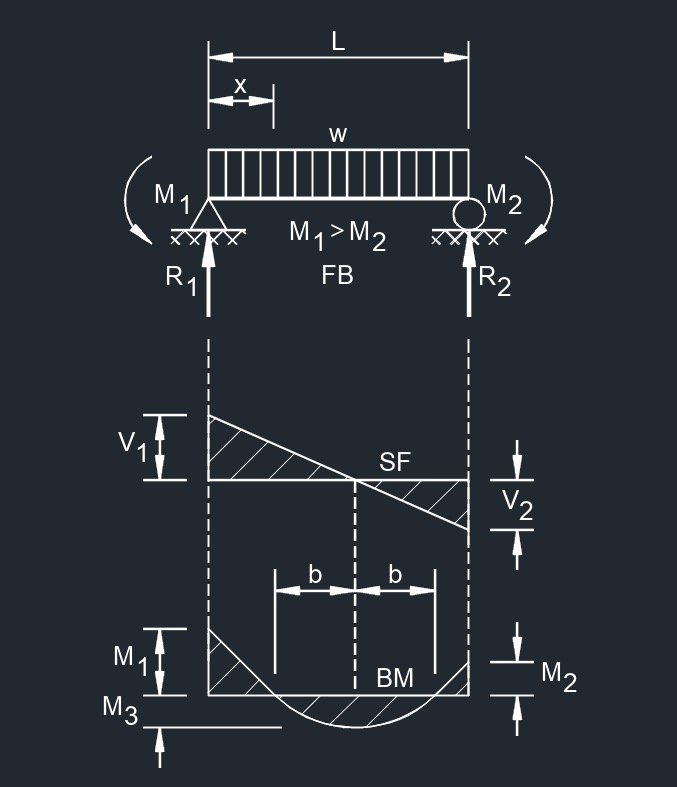Uniformly Distributed Load and Variable End Moments

 

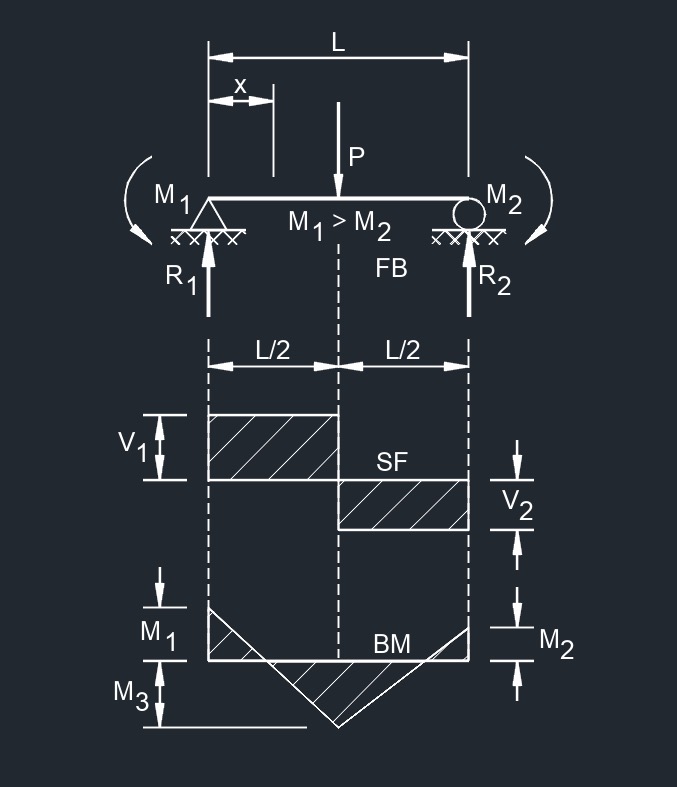Central Point Load and Variable End Moments

 

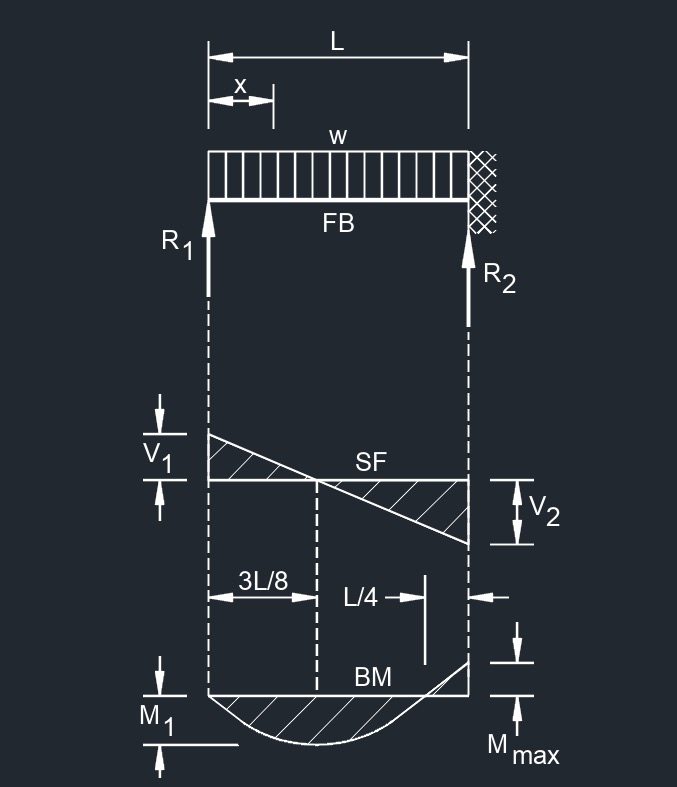
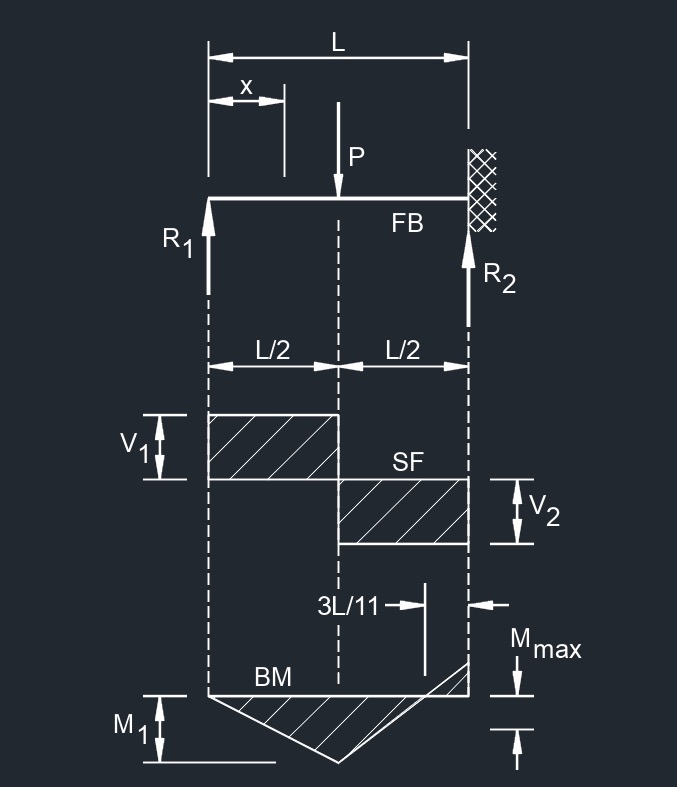
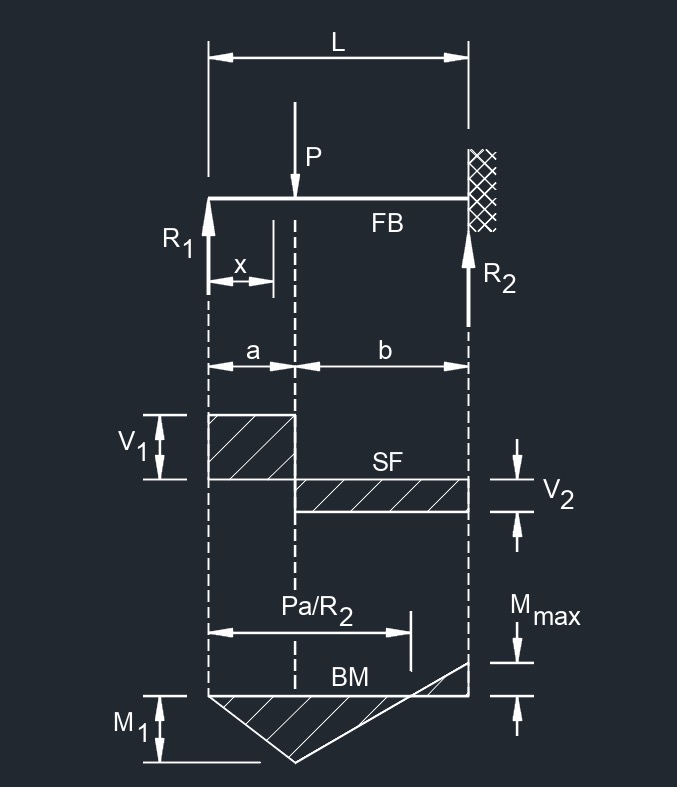
Beam Fixed at One End

Uniformaly Distributed LoadConcentrated Load at CenterConcentrated Load at Any Point

 

Beam Fixed at Both Ends

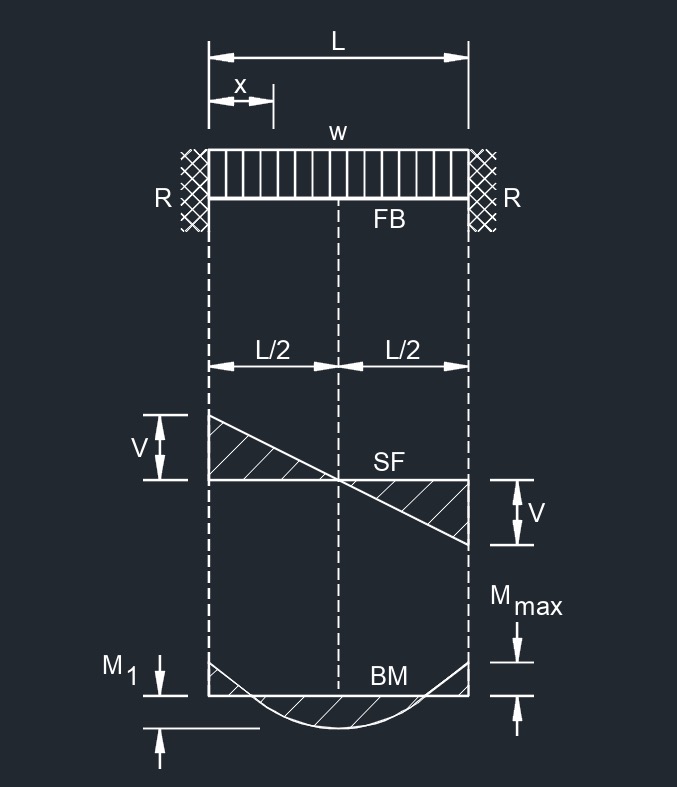Uniformaly Distributed Load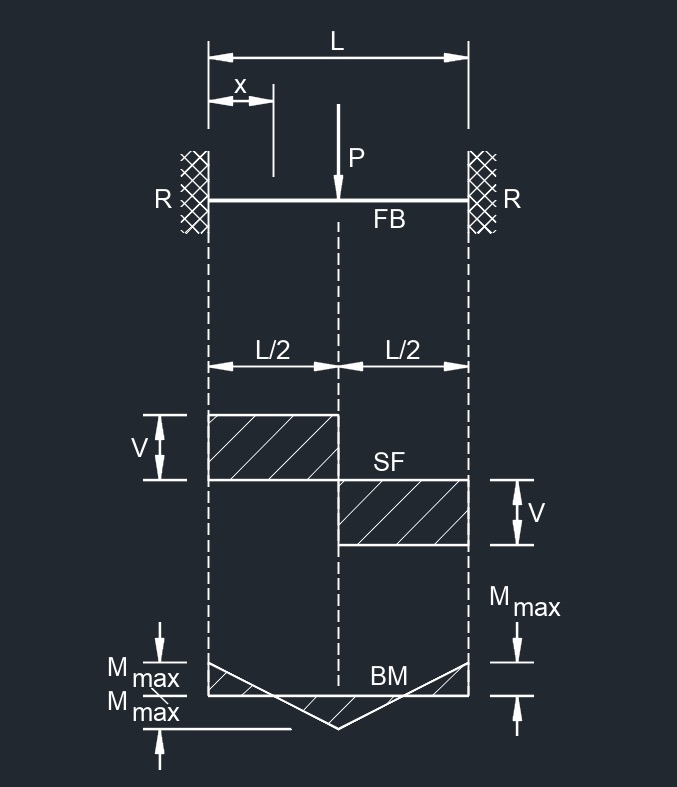Concentrated Load at Center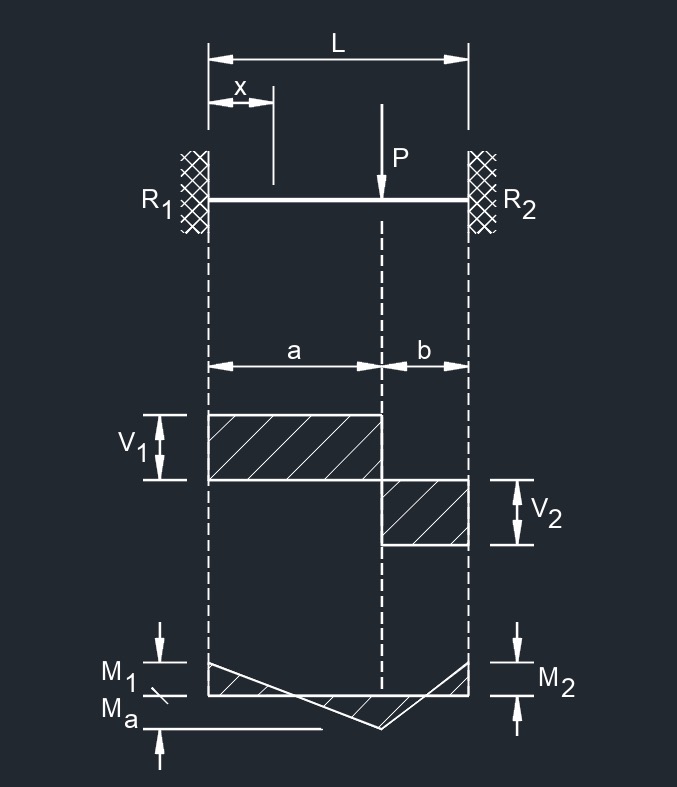Concentrated Load at Any Point

 

 

 

 

 

 

 

 

 

Cantilever Beam

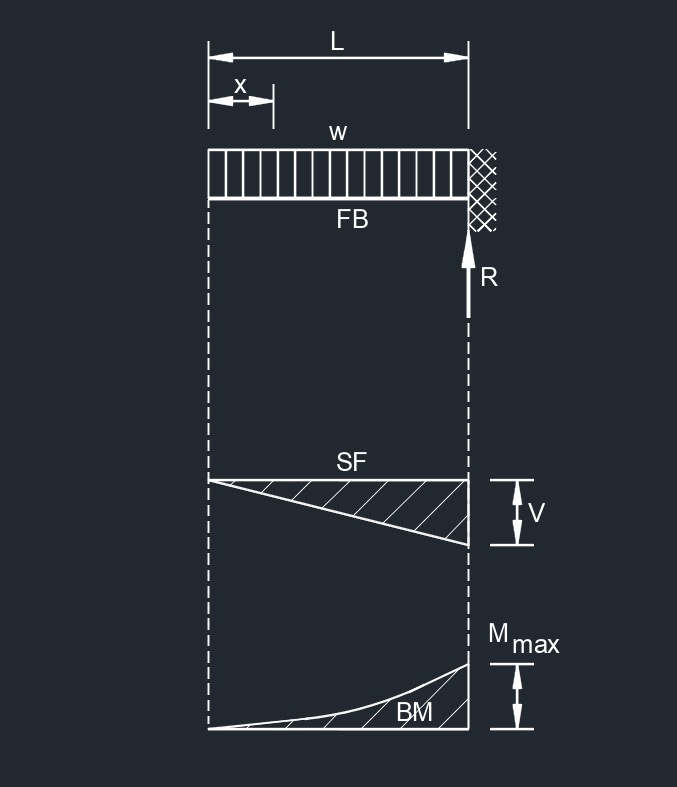Uniformaly Distributed Load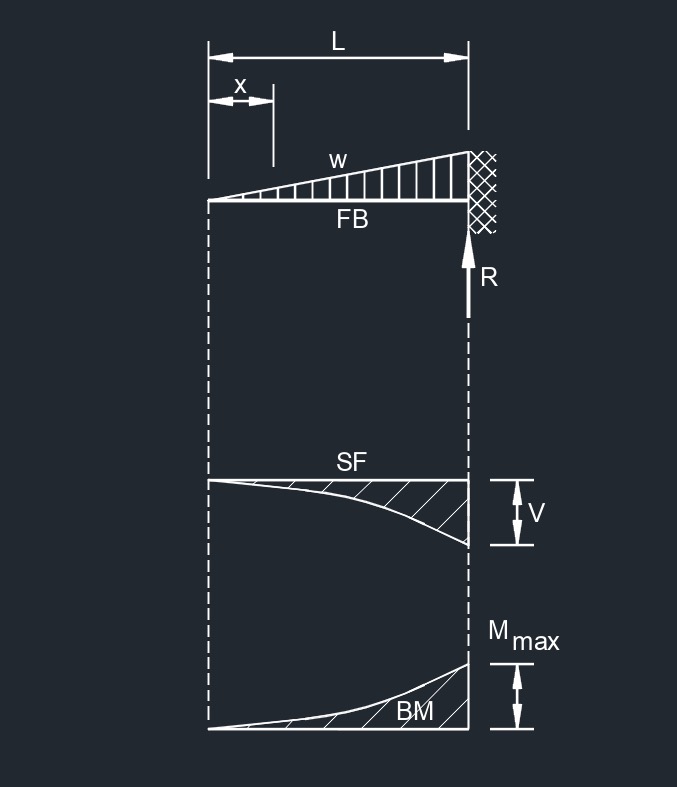Load Increasing Uniformly to One End 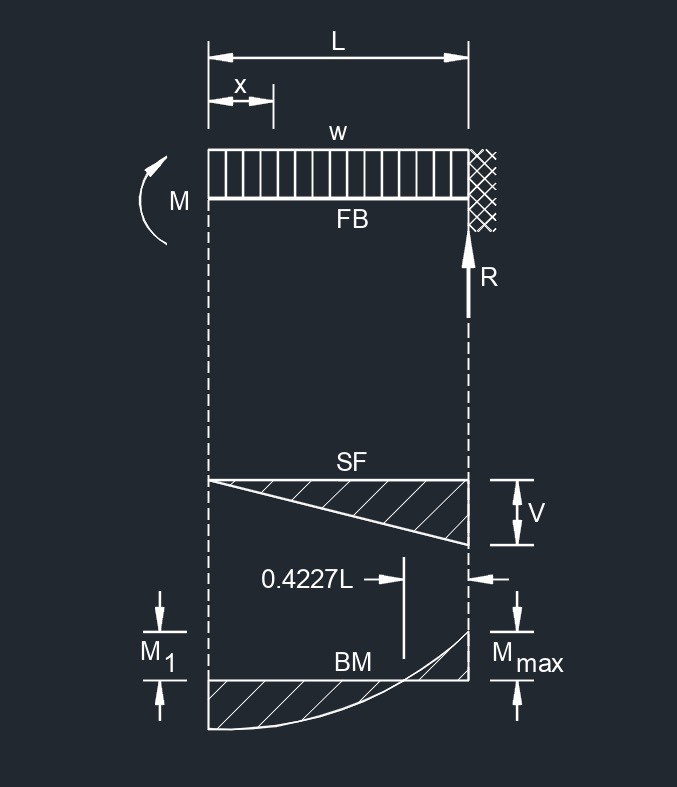Uniformly Distributed Load and Variable End Moments 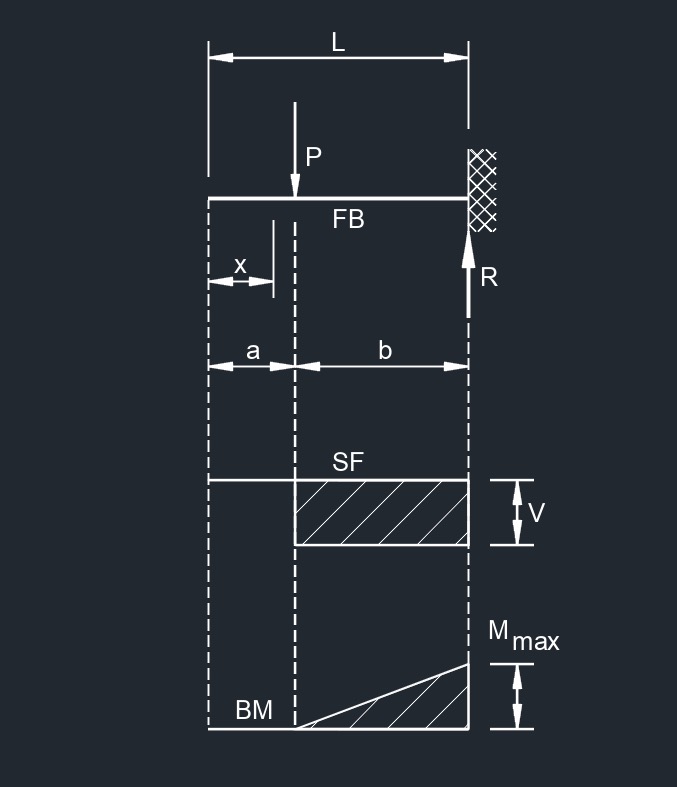Concentrated Load at Any Point

 

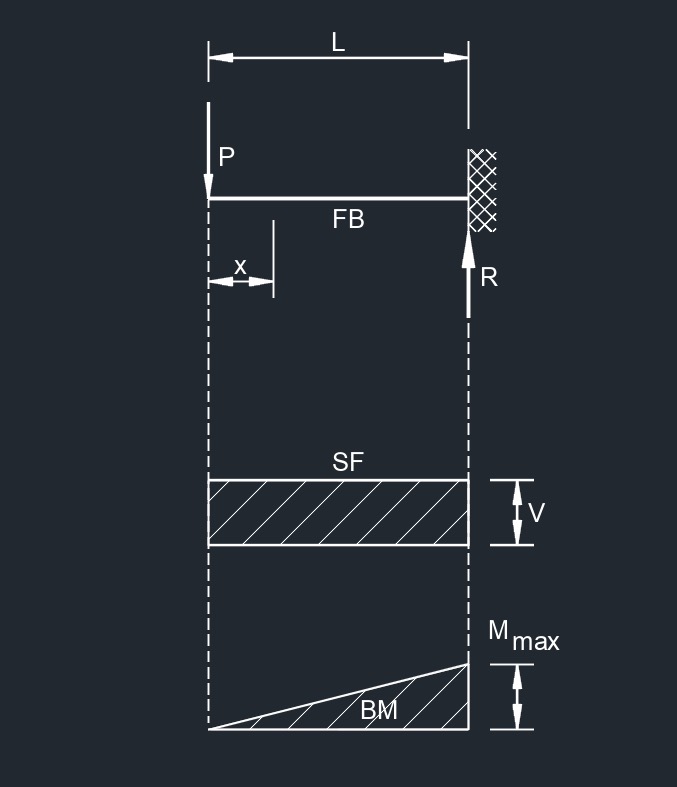Concentrated Load at Free End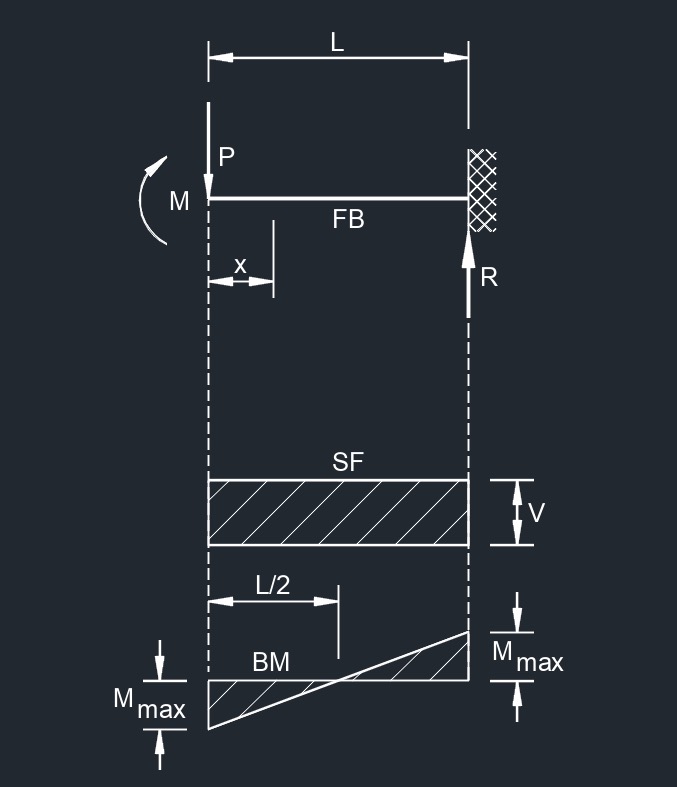Load at Free End Deflection Vertically with No Rotation

 

Overhanging Beam

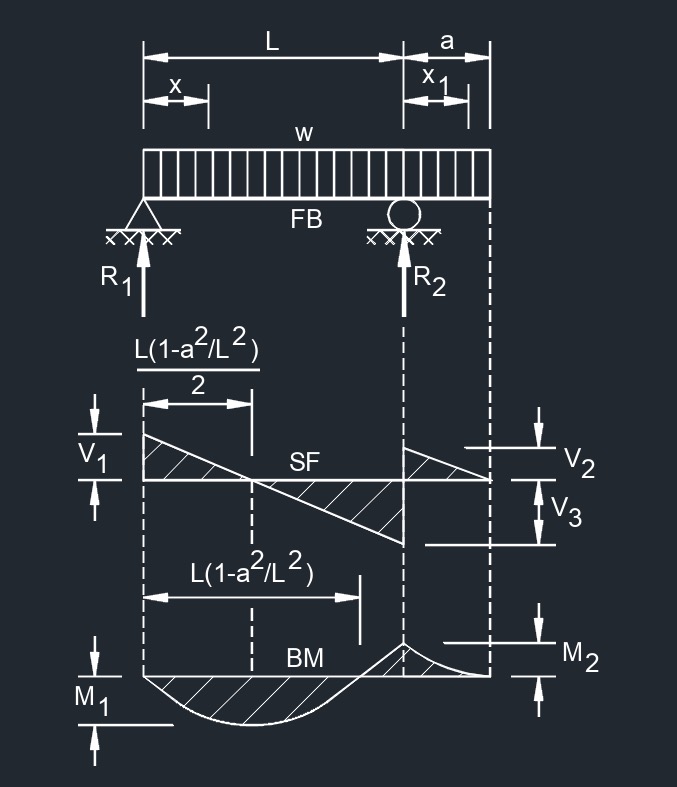Uniformly Distributed Load 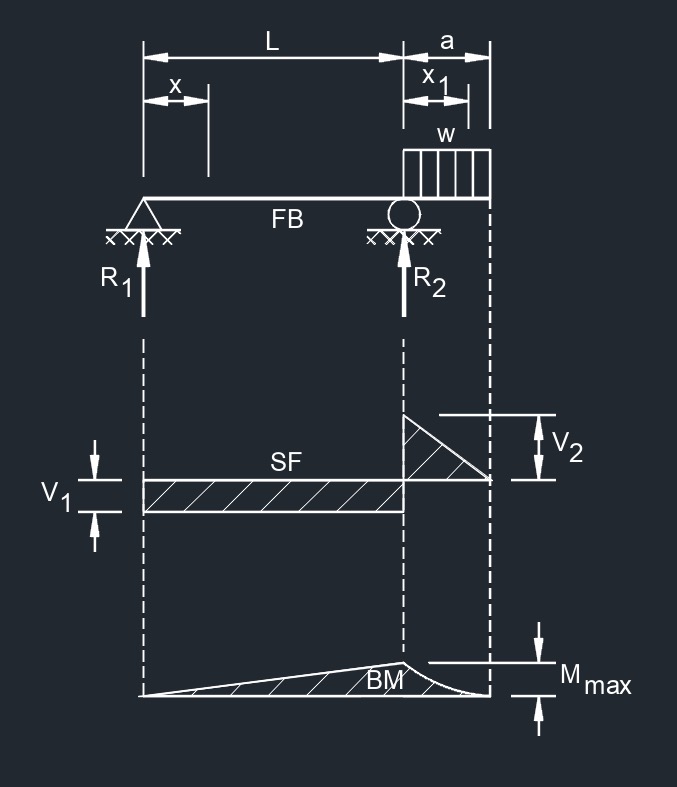Uniformly Distributed Load on Overhang 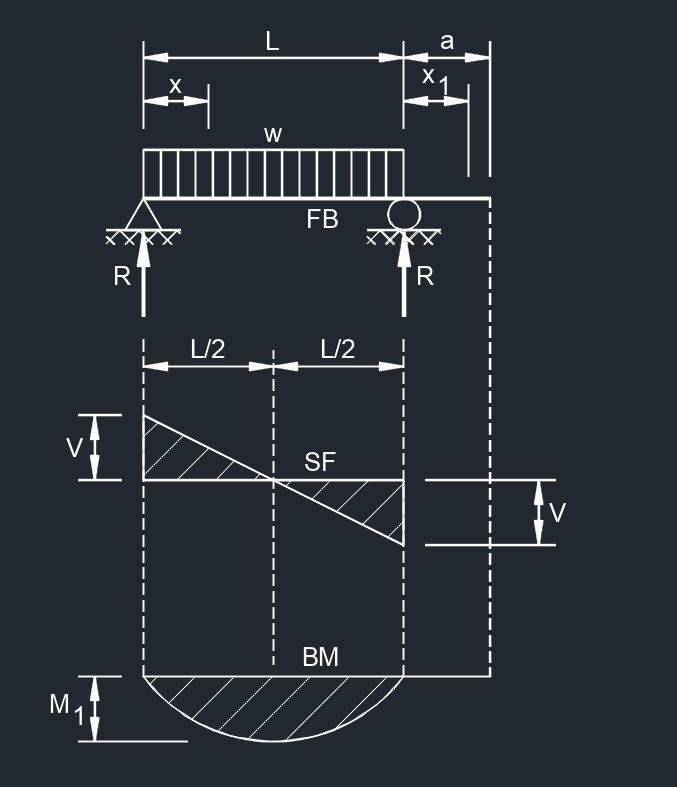Uniformly Distributed Load Over Supported Span 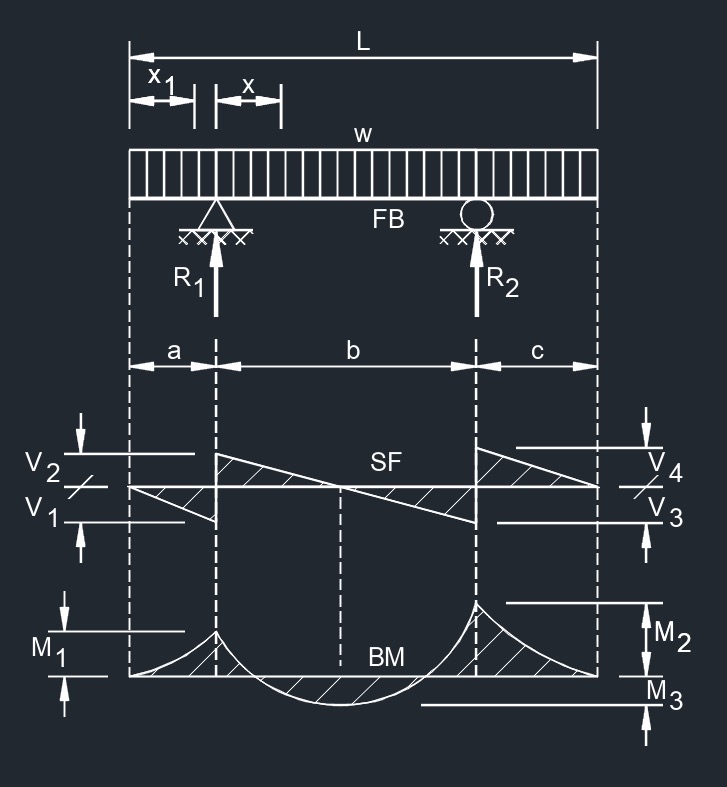Uniformly Distributed Load Overhanging Both Supports

 

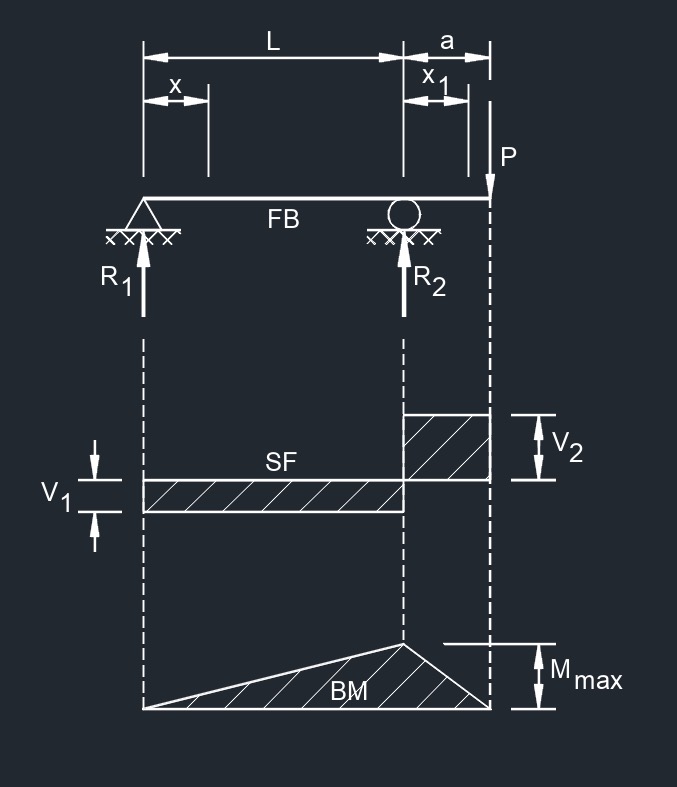Point Load on Beam End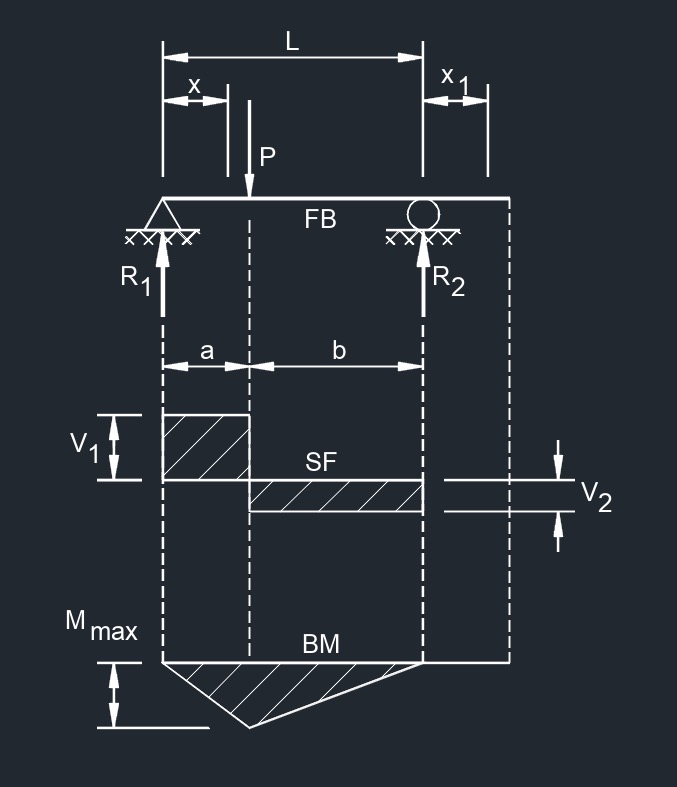Point Load Between Supports at Any Point

 

Two Span Continuous Beam

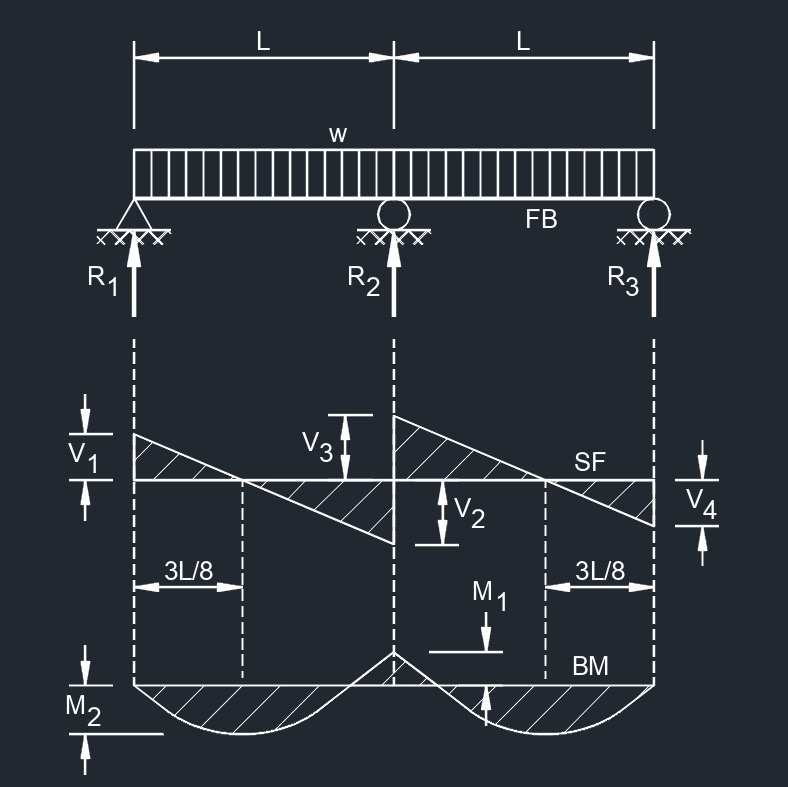Equal Spans, Uniformly Distributed Load 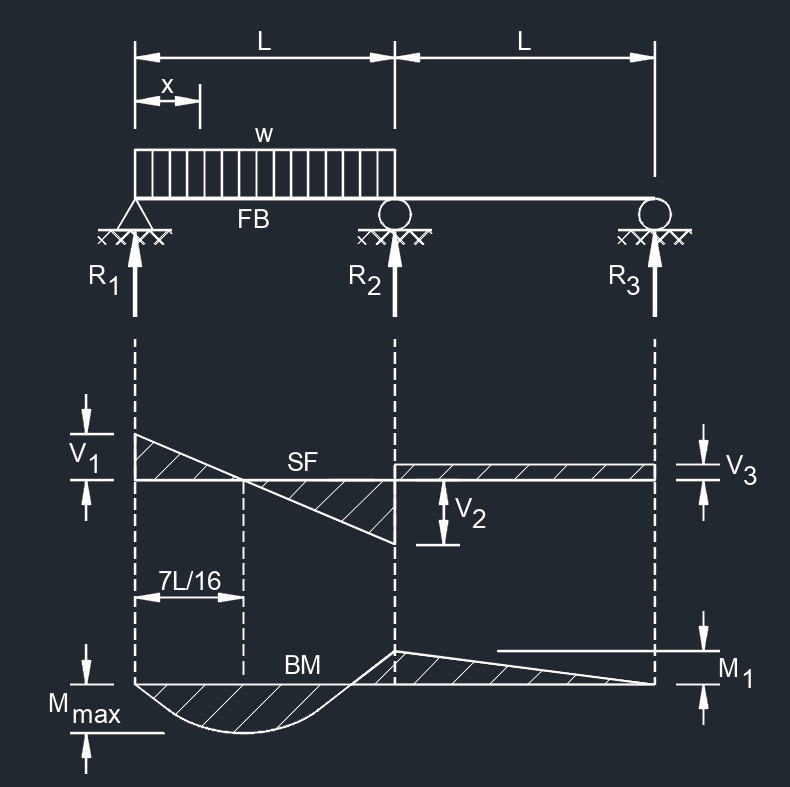Equal Spans, Uniform Load on One Span 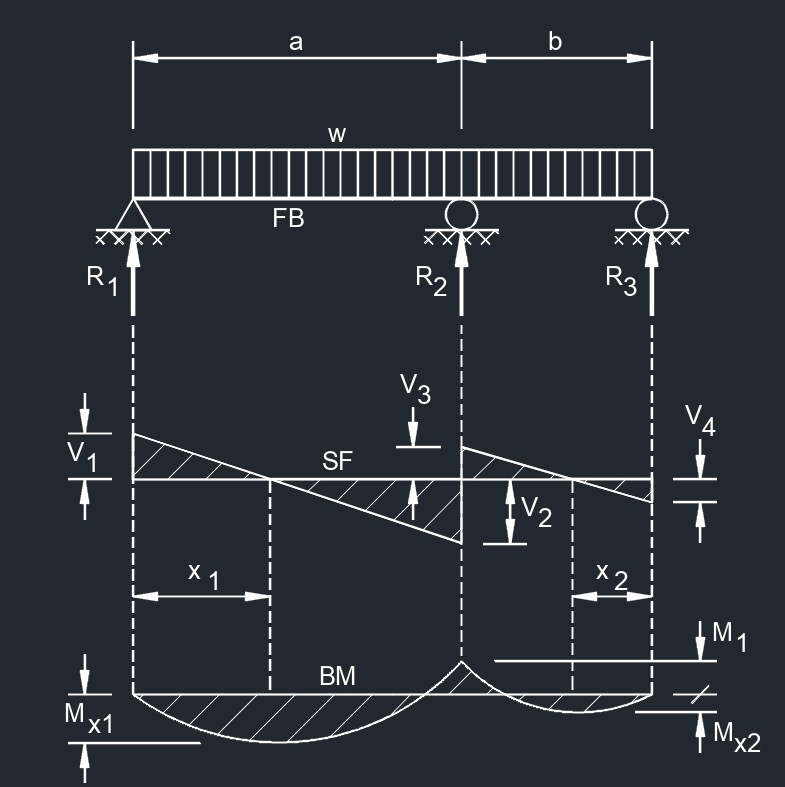Unequal Spans, Uniformly Distributed Load 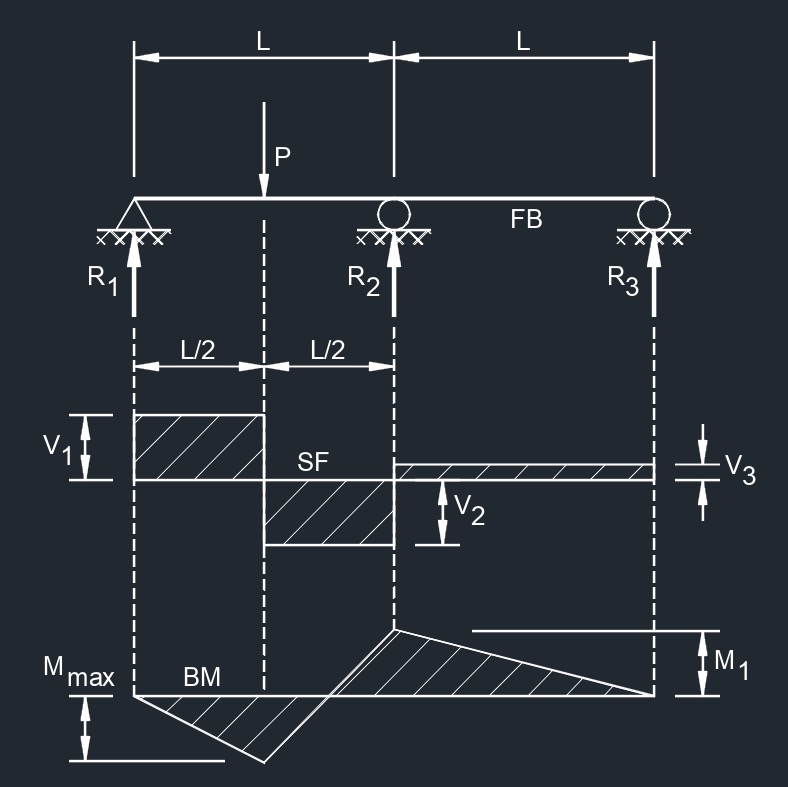Equal Spans, Concentrated Load at Center of One Span

 

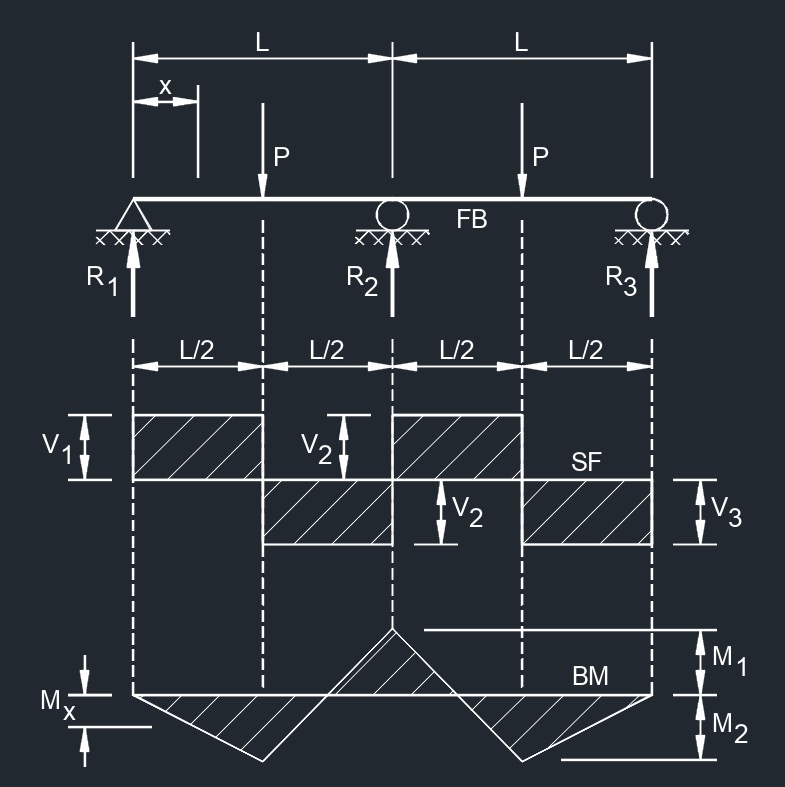Equal Spans, Two Equal Concentrated Loads Symmetrically Placed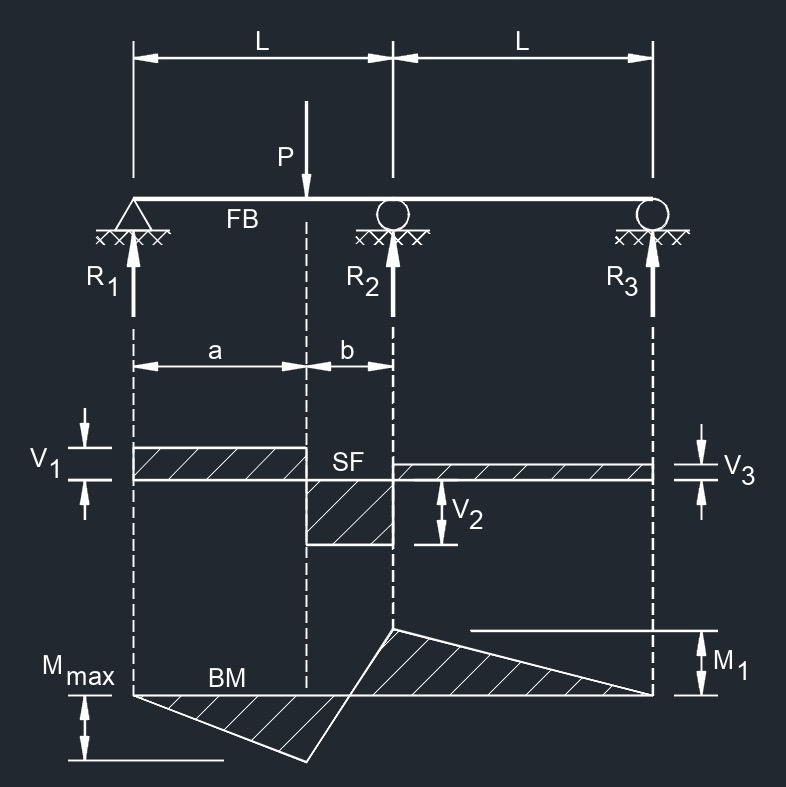Equal Spans, Concentrated Load at Any Point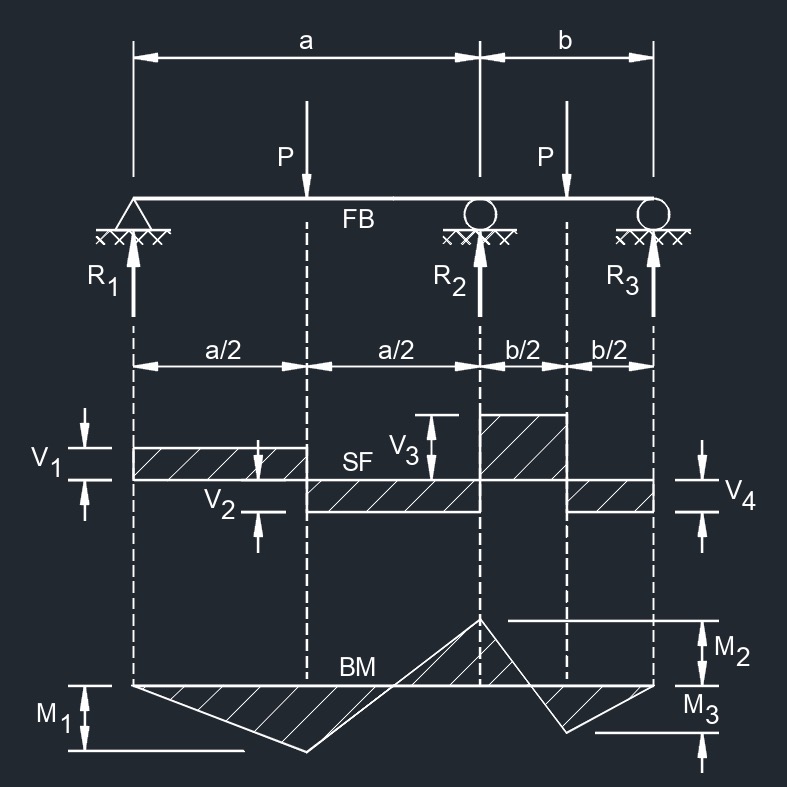Unequal Spans, Concentrated Load on Each Span Symmetrically Placed

 

Three Span Continuous Beam

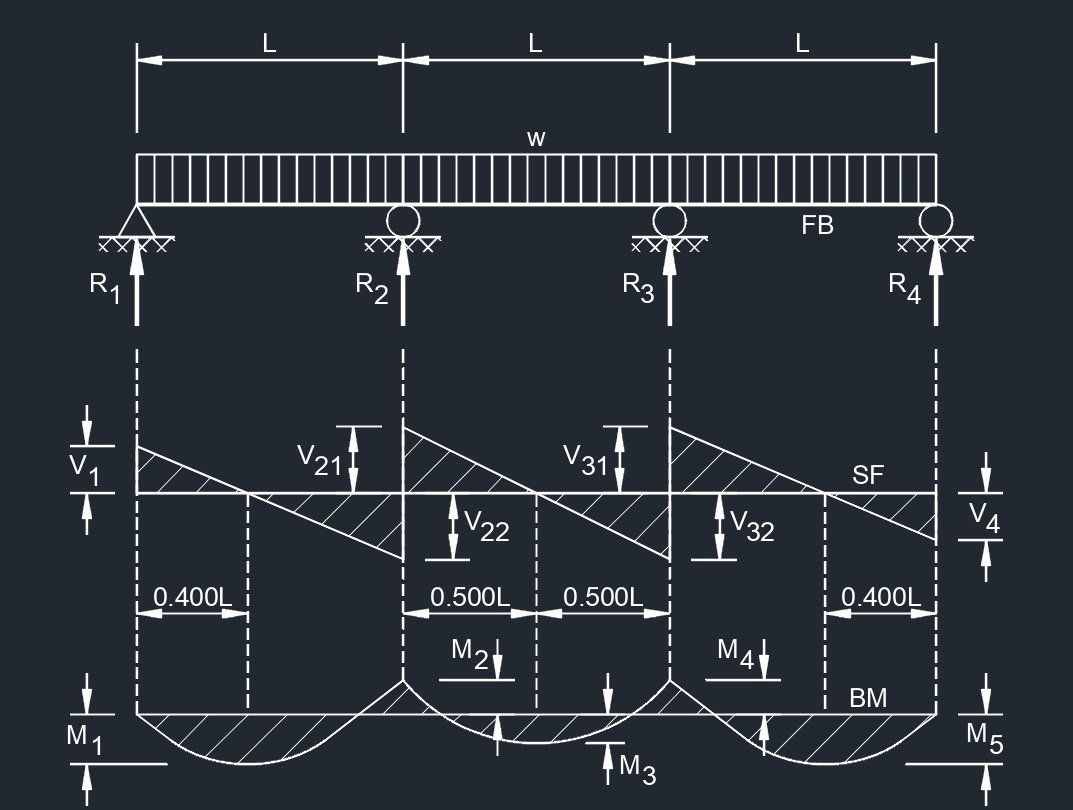Equal Spans, Uniformly Distributed Load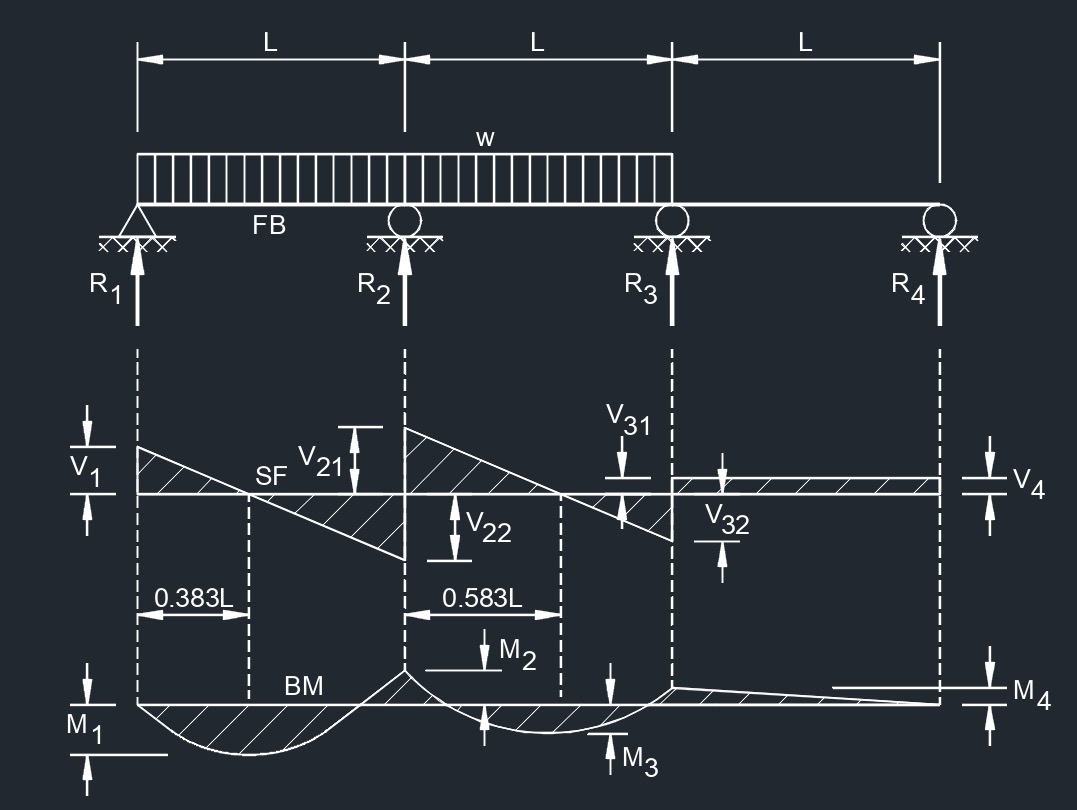Equal Spans, Uniform Load on Two Spans to One Side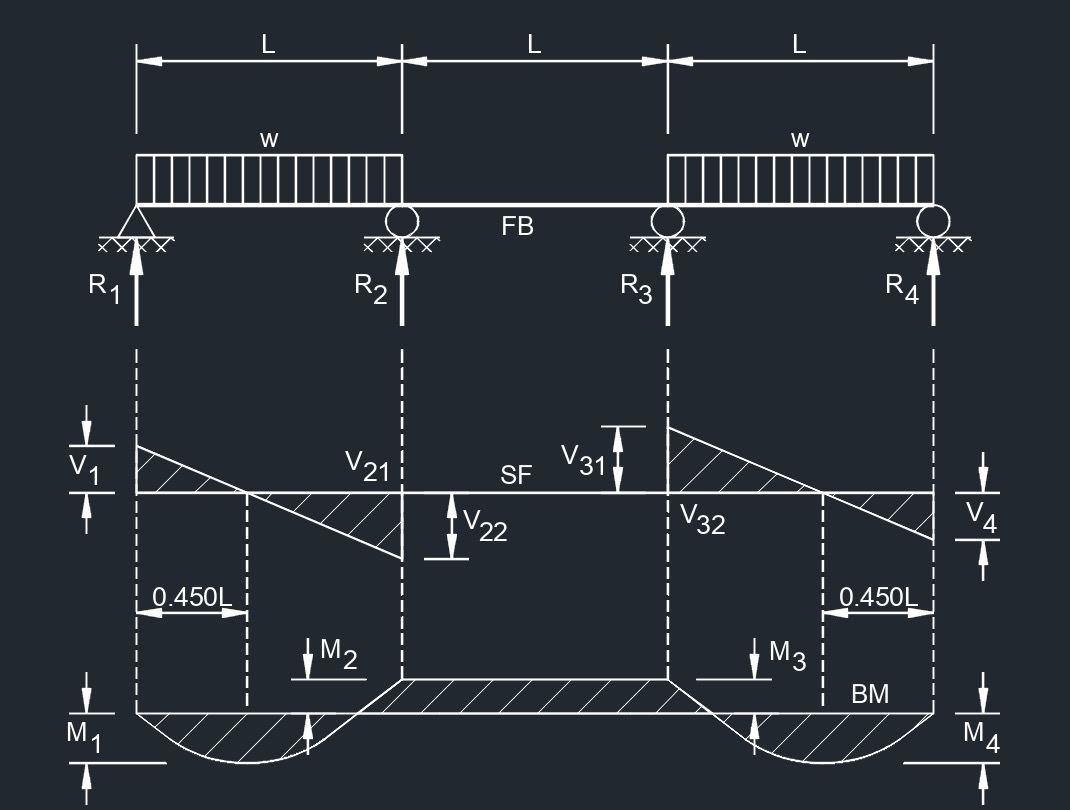Equal Spans, Uniform Load on Two Spans at Each End

 

Four Span Continuous Beam

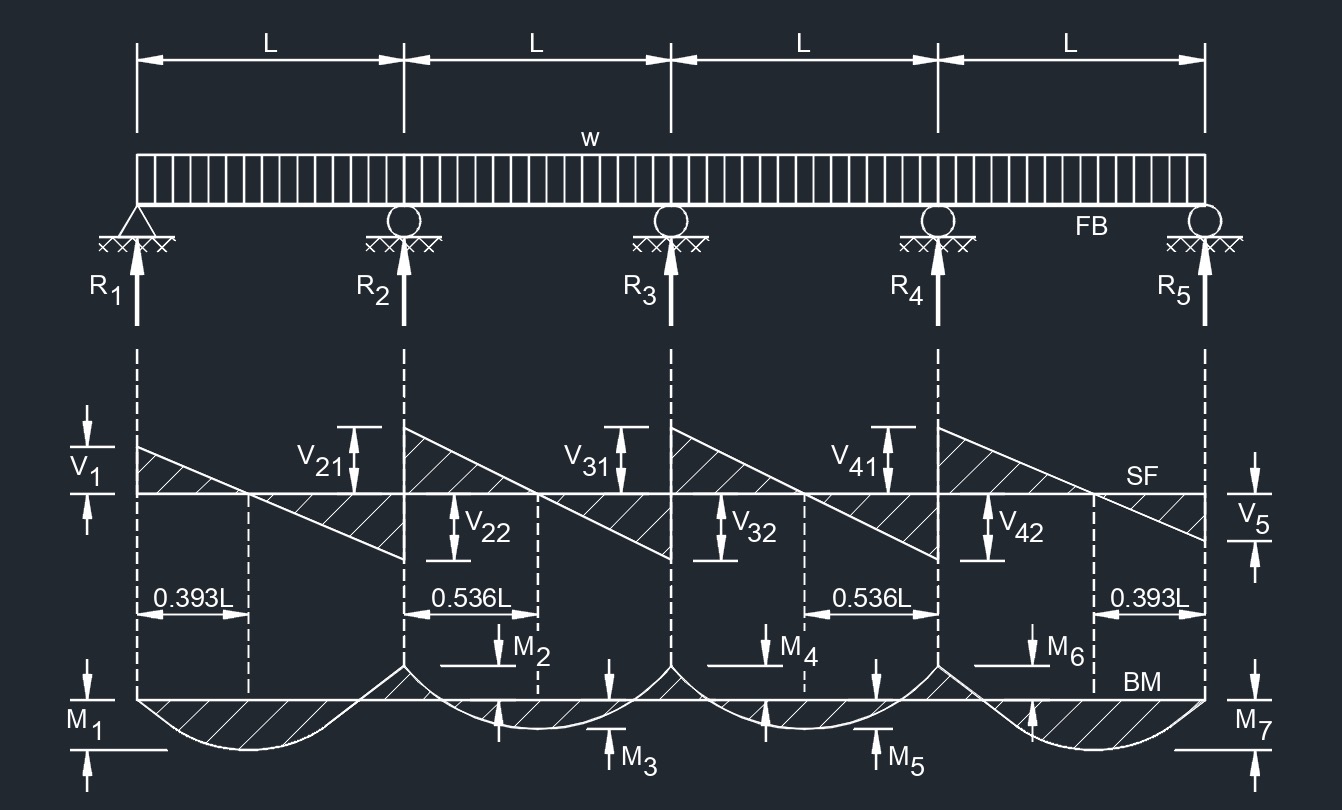Equal Spans, Uniformly Distributed Load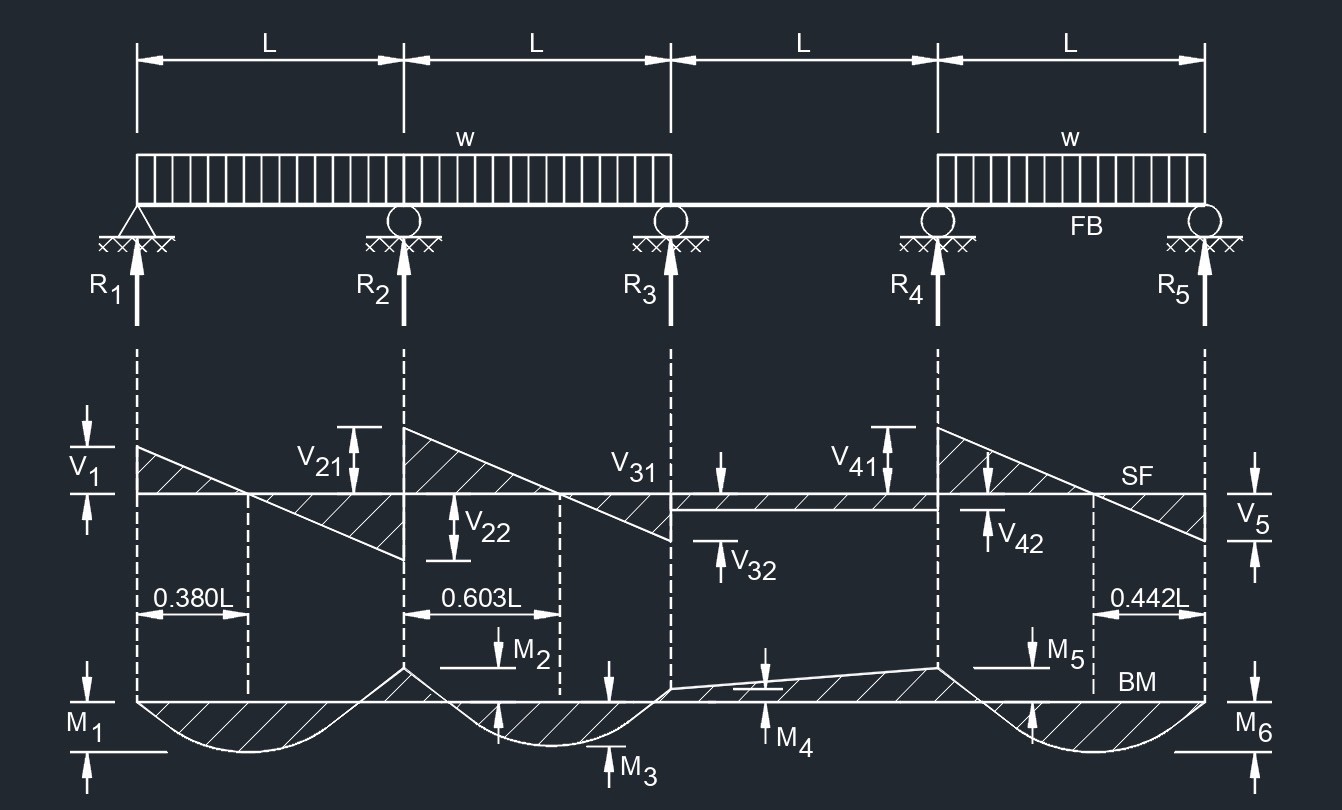Equal Spans, Uniform Load on Three Spans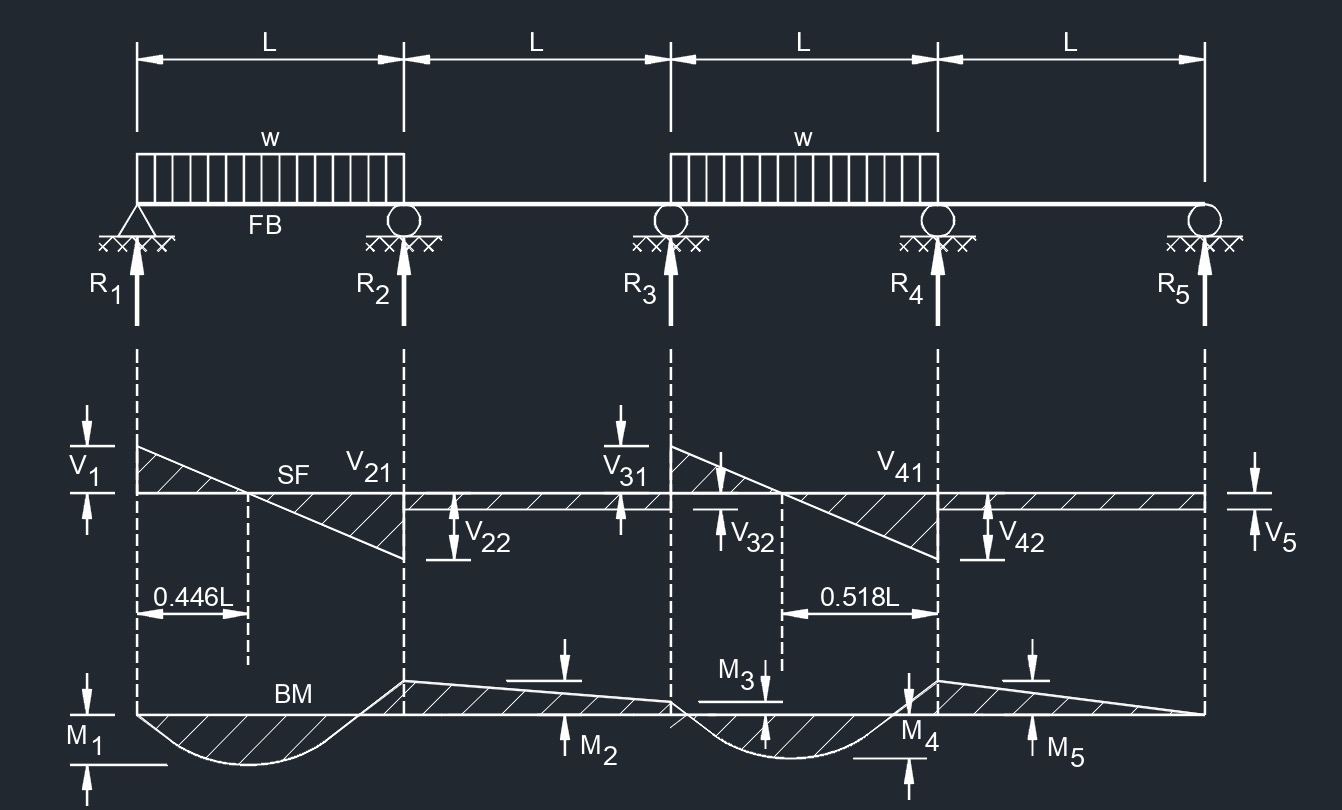Equal Spans, Uniform Load on Two Spans

 

 

Nomenclature, Symbols, and Units for Beam Supports
Symbol	Greek Symbol	Definition	English	Metric	SI	Value
\(\Delta\)	Delta	deflection or deformation	\(in\)	\(mm\)	\(mm\)	-
\(a, b\)	-	distance to point load	\(in\)	\(mm\)	\(mm\)	-
\(w\)	-	highest load per unit length	\(lbf\;/\;in\)	\(N\;/\;m\)	\(N-m^{-1}\)
\(x\)	-	horizontal distance from reaction to point on beam	\(in\)	\(mm\)	\(mm\)	-
\(w\)	-	load per unit length	\(lbf\;/\;in\)	\(N\;/\;m\)	\(N-m^{-1}\)	-
\(M\)	-	maximum bending moment	\(lbf-in\)	\(N-mm\)	\(N-mm\)	-
\(V\)	-	maximum shear force	\(lbf\)	\(N\)	\(kg-m-s^{-2}\)
\(\lambda\)	lambda	modulus of elasticity	\(lbf\;/\;in^2\)	\(MPA\)	\(N-mm^{-2}\)	-
\(R\)	-	reaction load at bearing point	\(lbf\)	\(N\)	\(kg-m-s^{-2}\)	-
\(I\)	-	second moment of area (moment of inertia)	\(in^4\)	\(mm^4\)	\(mm^4\)	-
\(L\)	-	span length of the bending member	\(in\)	\(mm\)	\(mm\)	-
\(P\)	-	total concentrated load	\(lbf\)	\(N\)	\(kg-m-s^{-2}\)	-
\(W\)	-	total load \(\left( \frac{w\;L}{2} \right)\)	\(lbf\)	\(N\)	\(kg-m-s^{-2}\)	-