Skip to main content

Frame Design Formulas

Diagram Symbols

Bending moment diagram (BMD)  -  Used to determine the bending moment at a given point of a structural element.  The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Free body diagram (FBD)  -  Used to visualize the applied forces, moments, and resulting reactions on a structure in a given condition.
Shear force diagram (SFD)  -  Used to determine the shear force at a given point of a structural element.  The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Uniformly distributed load (UDL)  -  A load that is distributed evenly across the entire length of the support area.

Two Member Frame - Fixed/Fixed

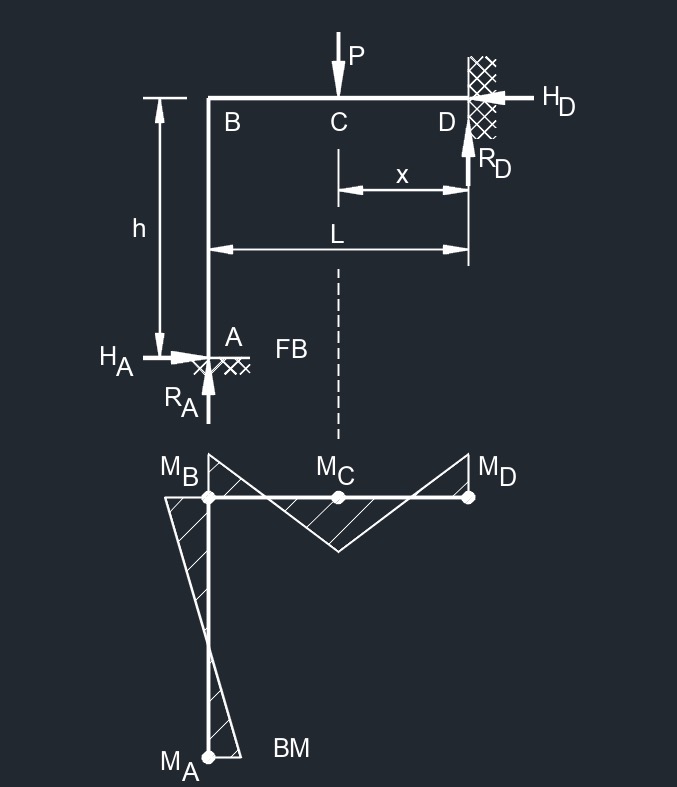2ffbe 1Top Point Load 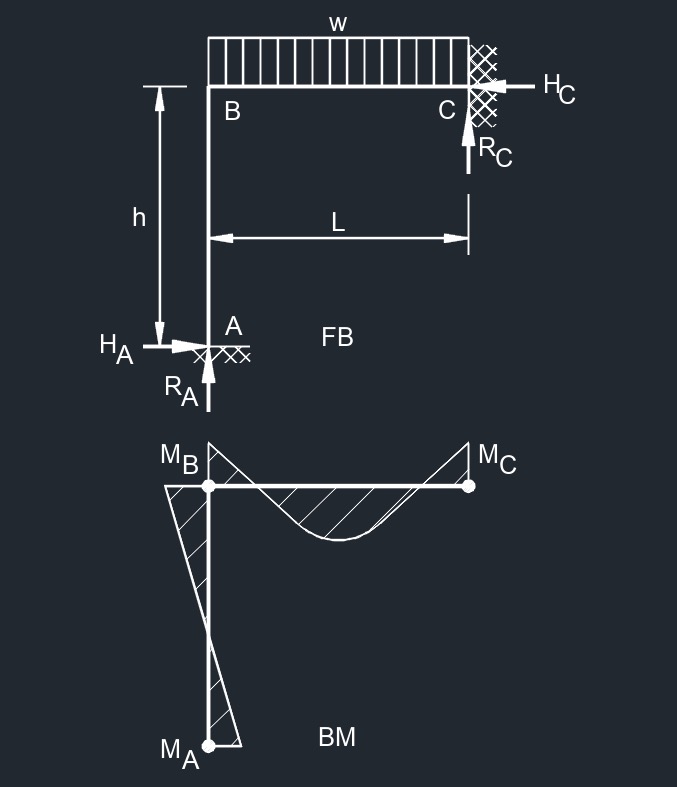2ffbe 2Top Uniformaly Distributed Load

 

 

 

 

 

Two Member Frame - Fixed/Free

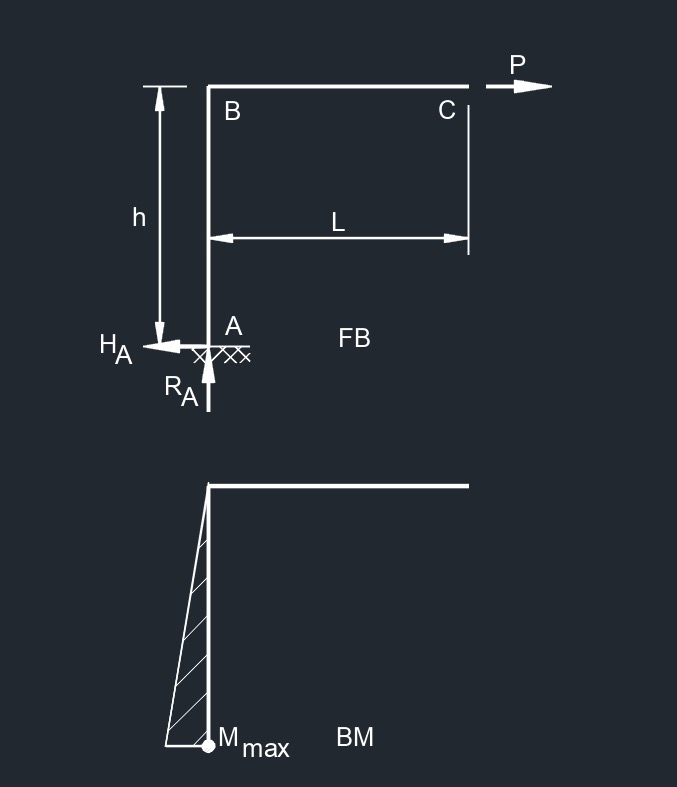2fff 2Free End Horizontal Point Load 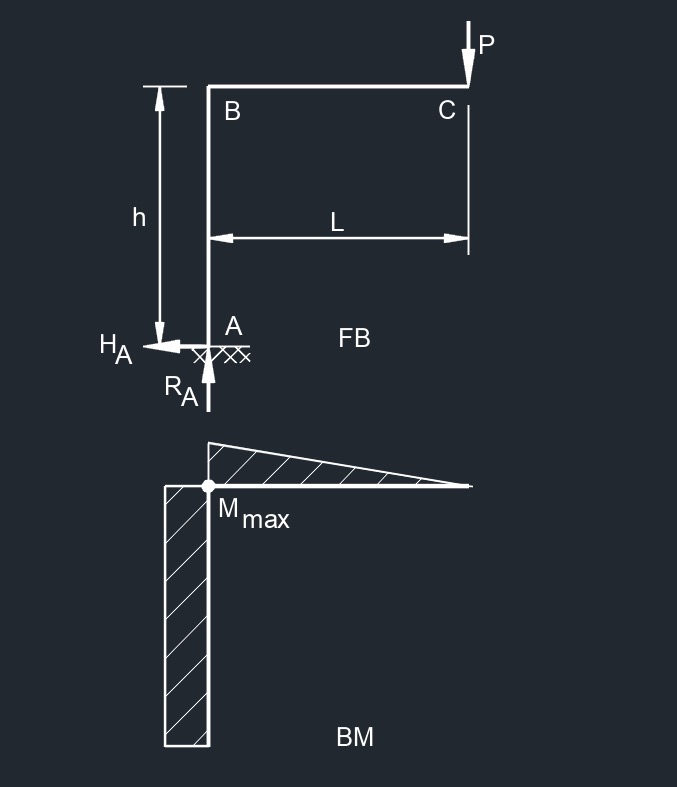2fff 1Free End Vertical Point Load 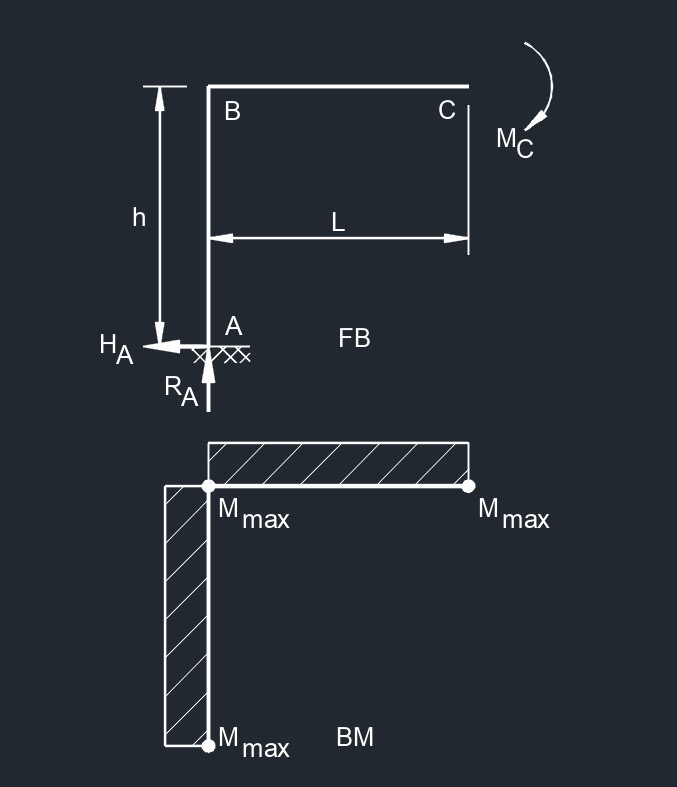2fff 3A Free End Bending Moment 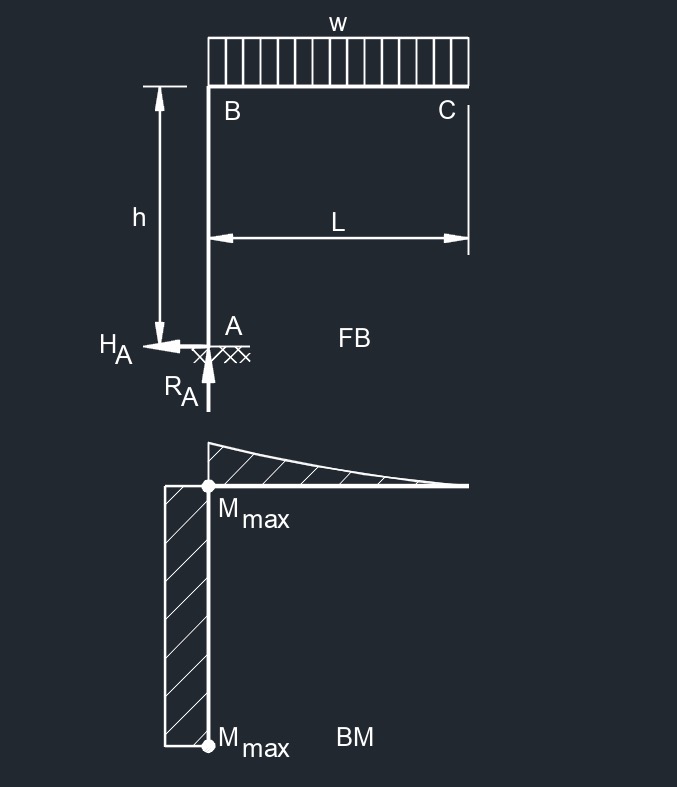2fff 4Top Uniformaly Distributed Load

 
 
 
 
 

Two Member Frame - Fixed/Pin

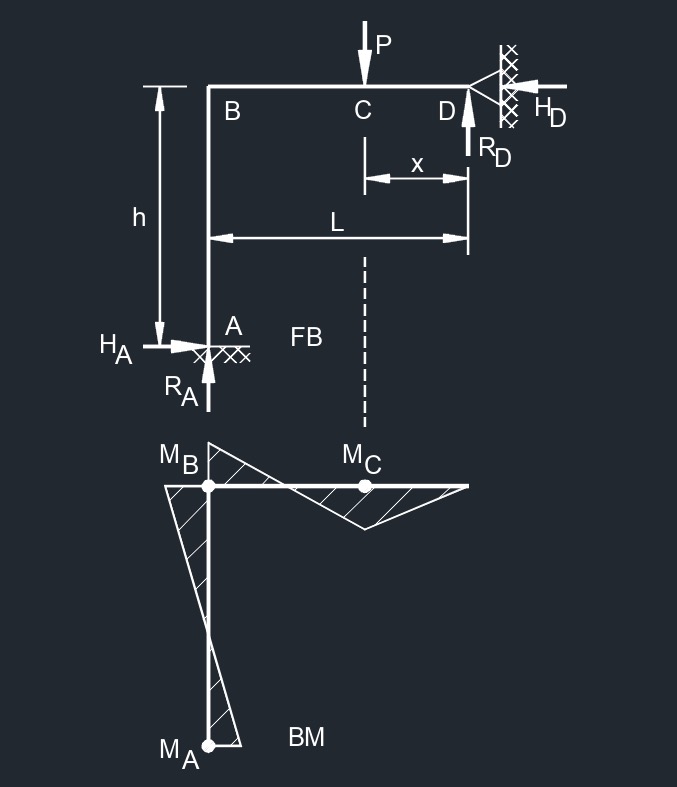2ffp 1ATop Point Load 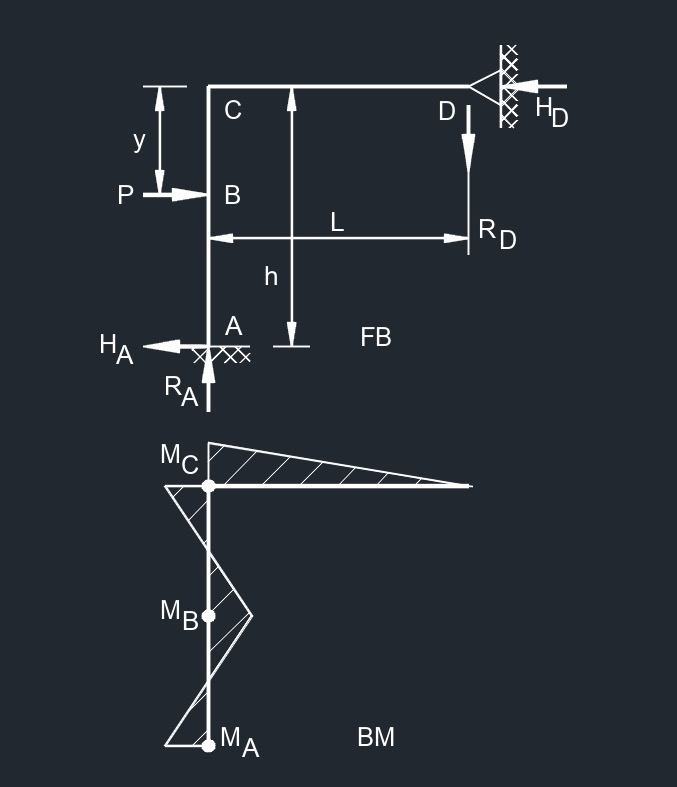2ffp 2Side Point Load 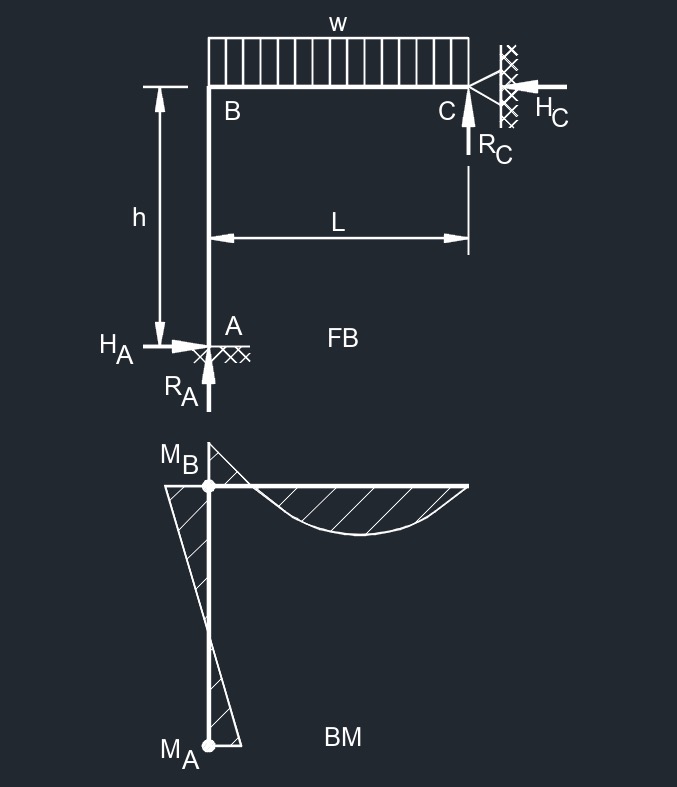2ffp 3A Top Uinformaly Distributed Load 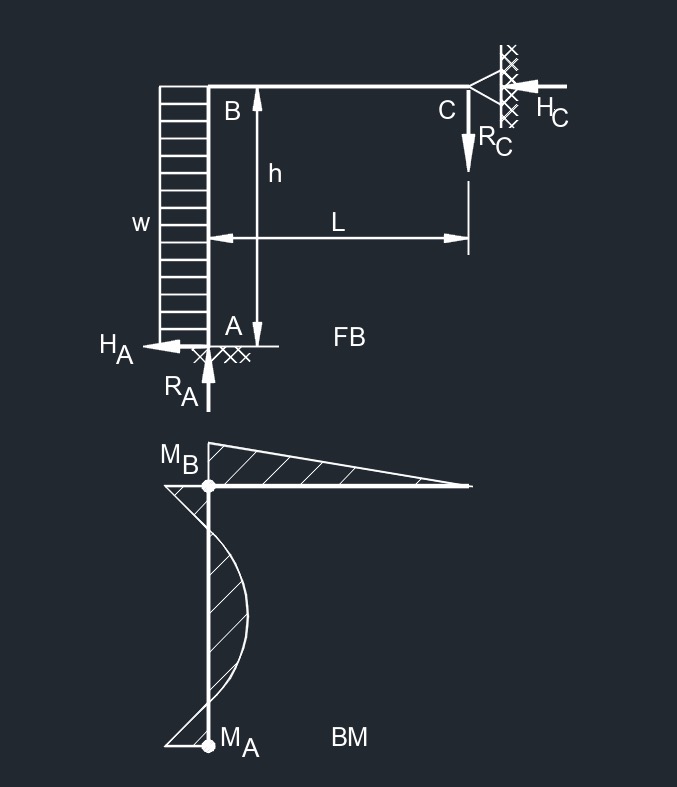2ffp 4ASide Uniformaly Distributed Load

 

 

 

 

 

 

 

 

Two Member Frame - Pin/Pin

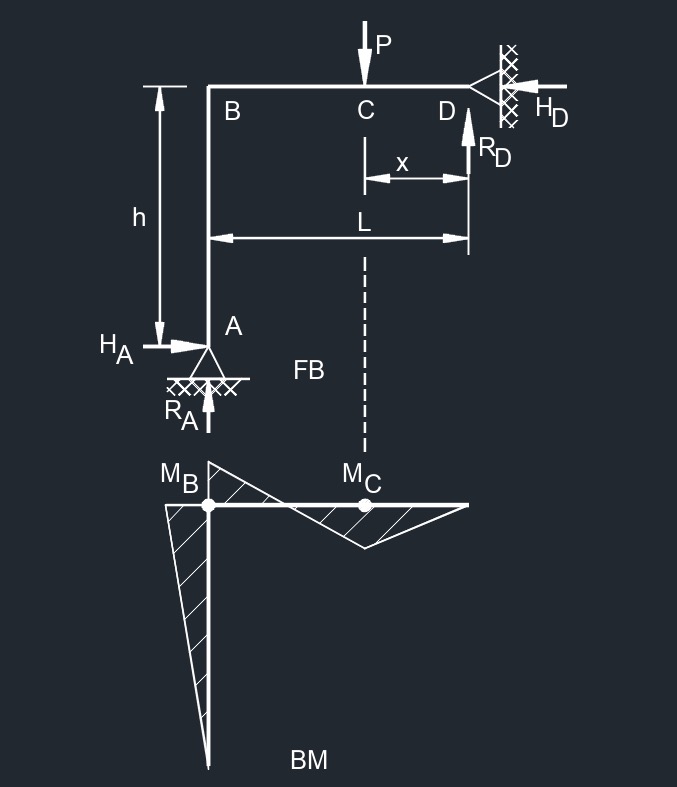dummy 200x200Top Ppint Load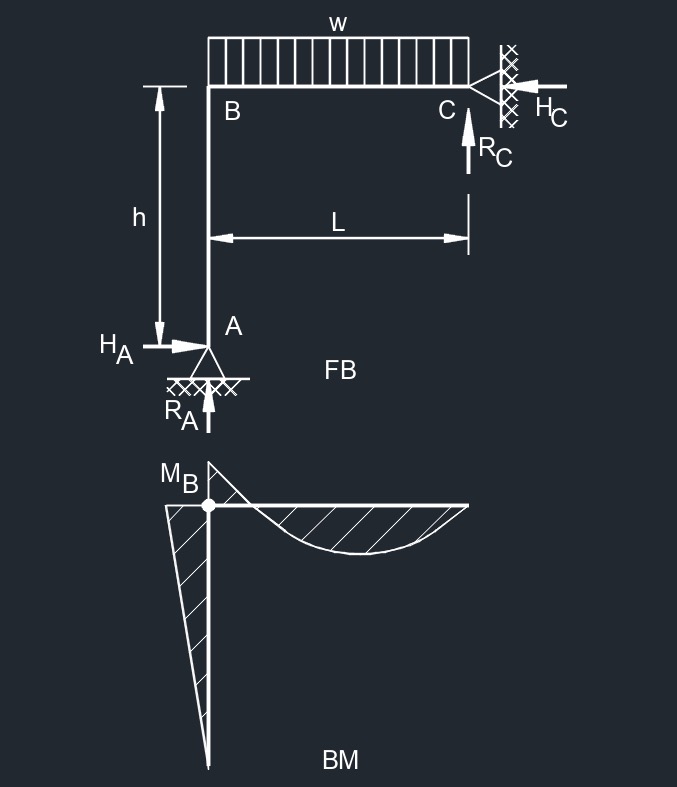dummy 200x200Top Uniformaly Distributed Load

 

 

 

 

 

 

 

 

Three Member Frame - Fixed/Fixed

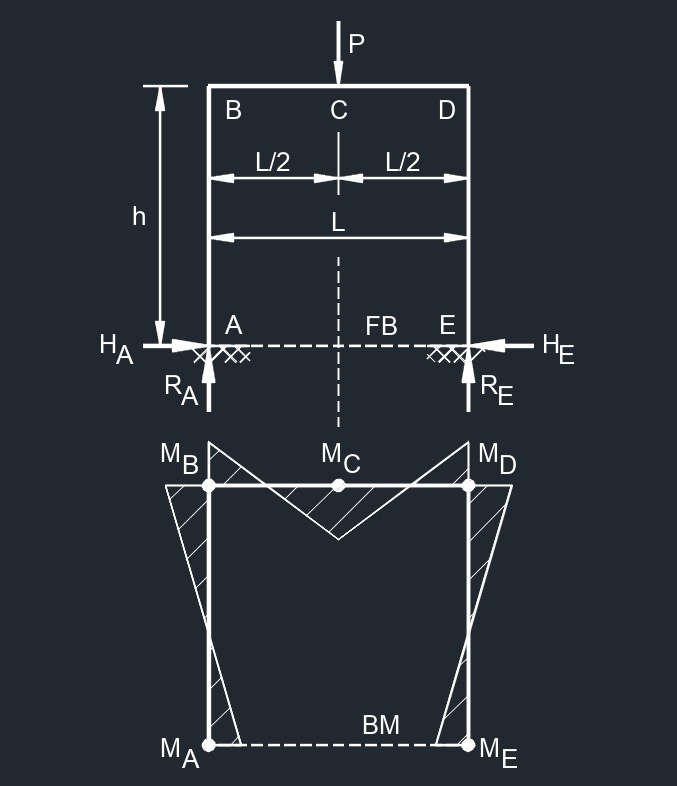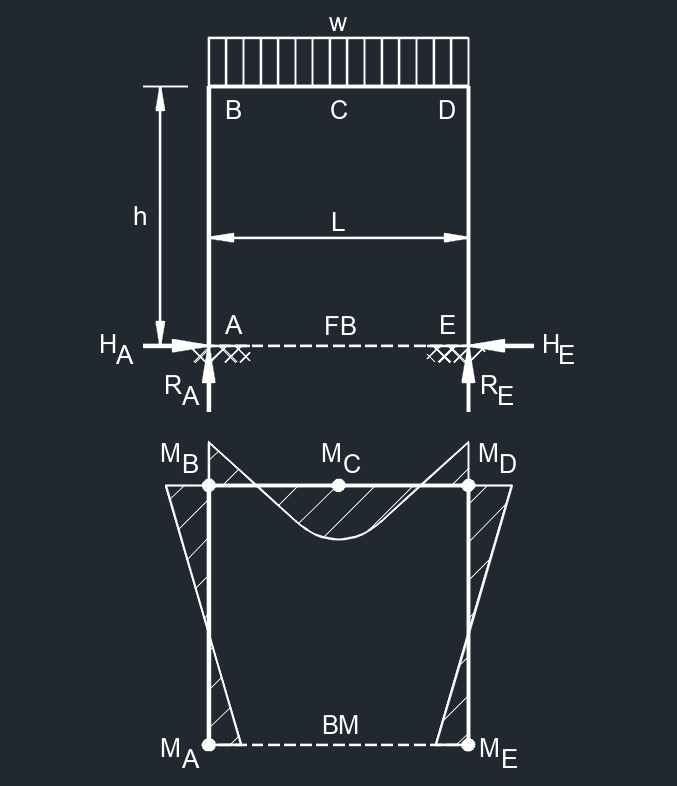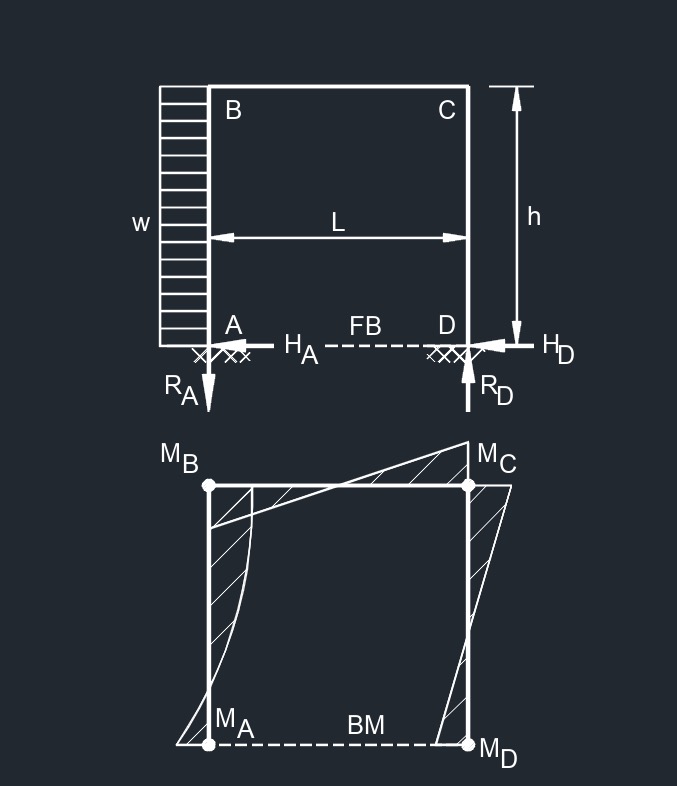3fbe 2Center Point Load 3fbe 1Top Uniformaly Distributed Load 3fbe 3Side Uniformaly Distributed Load

 

 

 

 

 

Three Member Frame - Fixed/Free

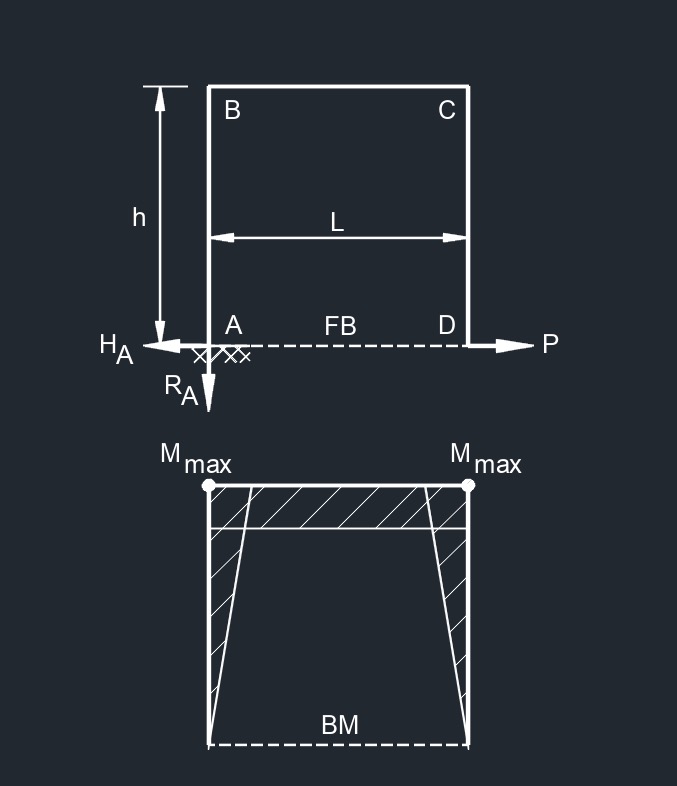3fff 1Free End Horizontal Point Load 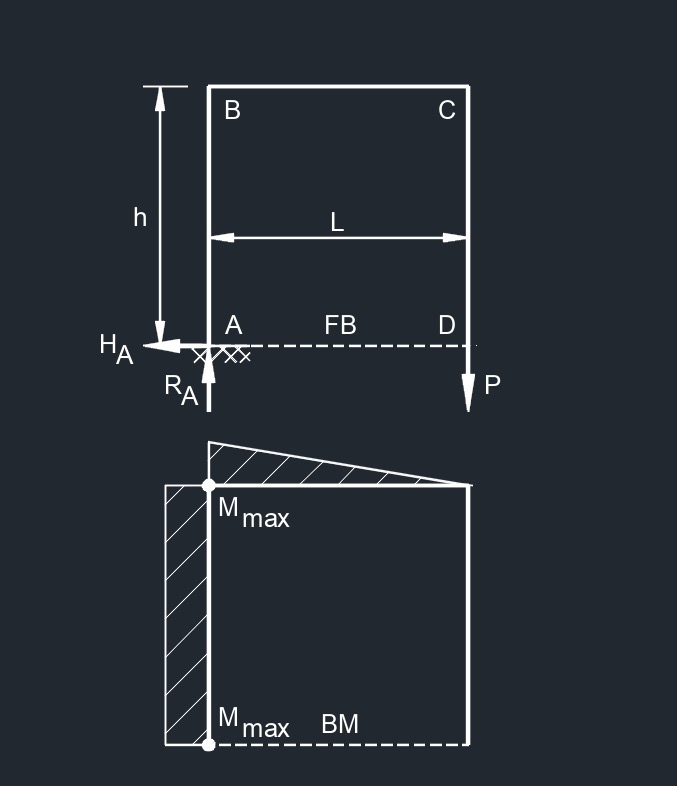3fff 2Free End Vertical Point Load 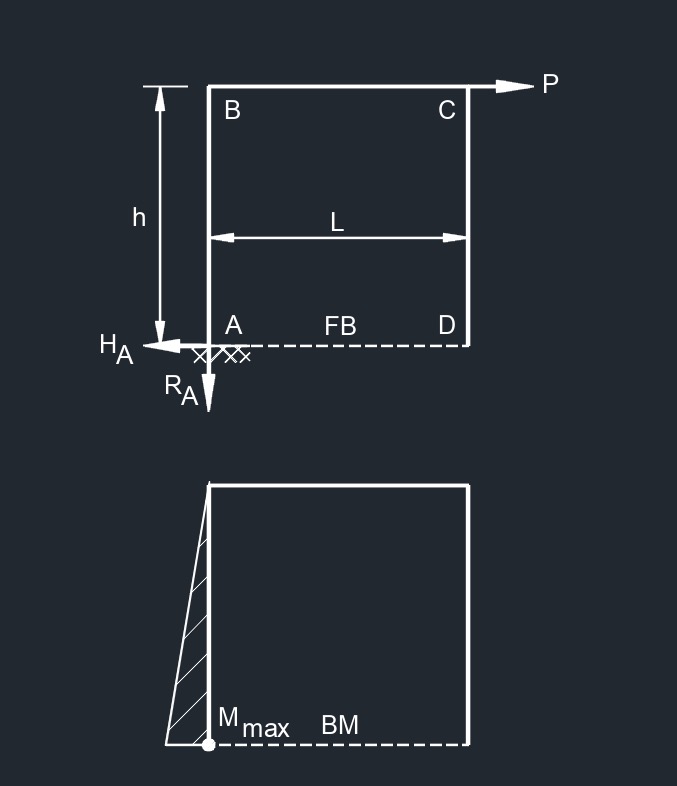3fff 3Side Top Point Load 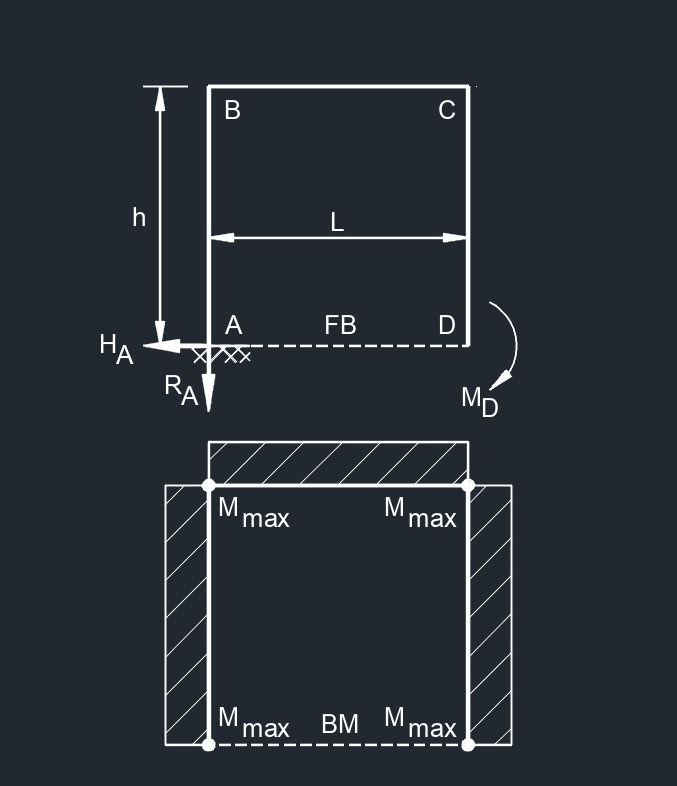3fff 4Free End Bending Moment

 

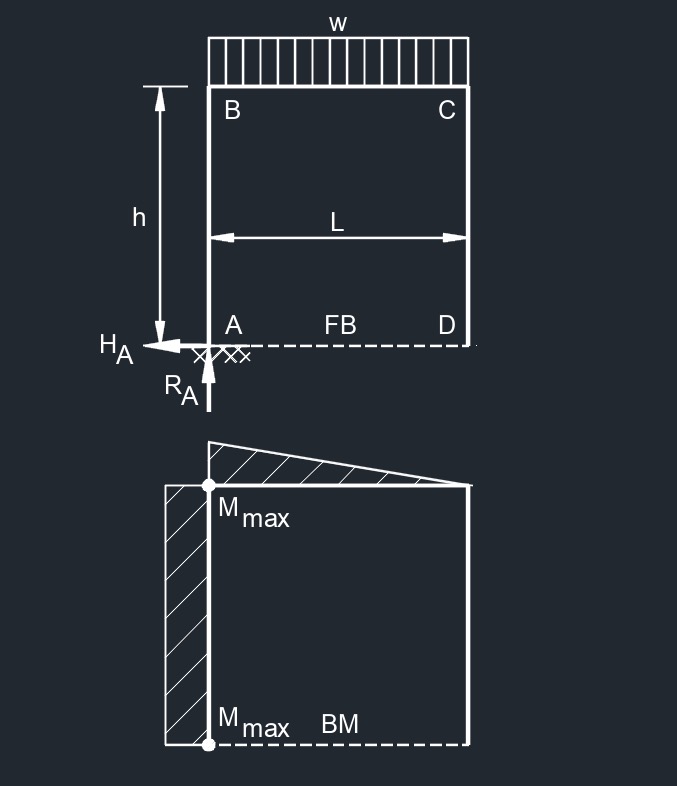3fff 5Top Uniformaly Distributed Load

 

 

 

 

 

 

 

Three Member Frame - Pin/Pin

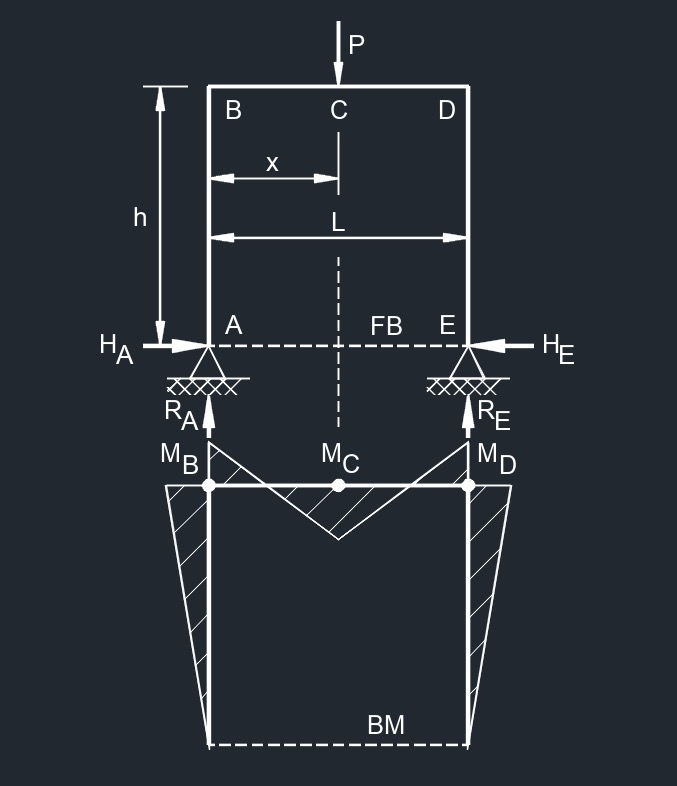3fpbe 1Top Point Load 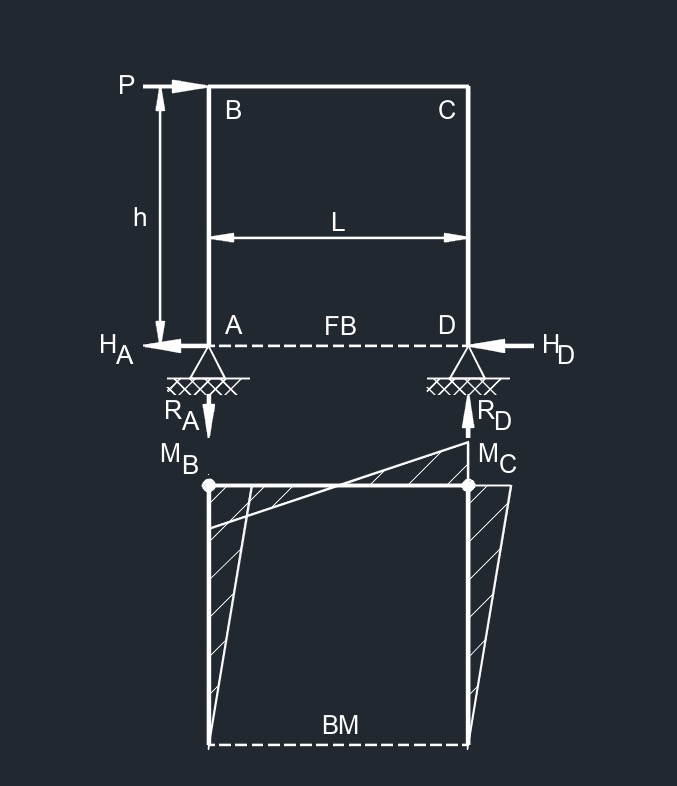3fpbe 2Top Horizontal Point Load 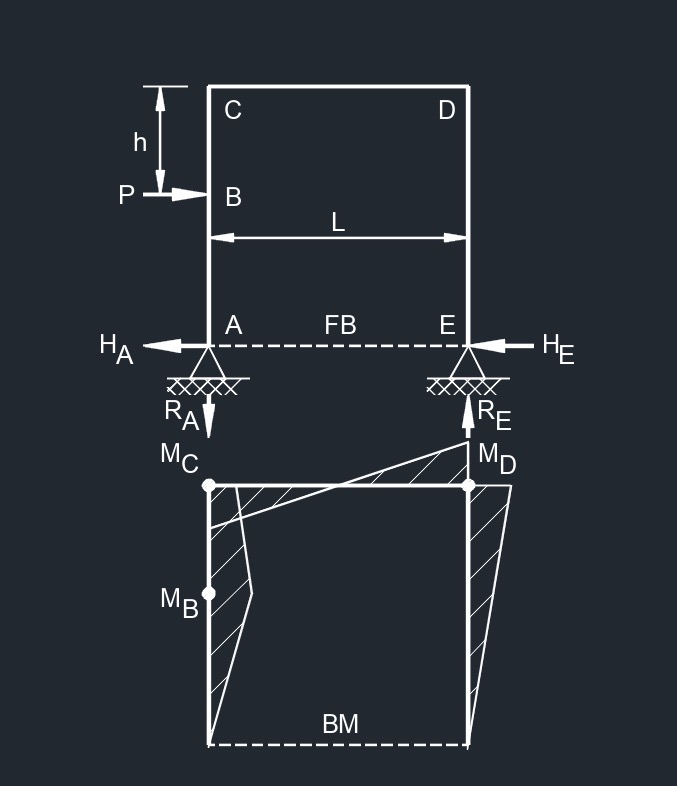3fpbe 3Side Point Load 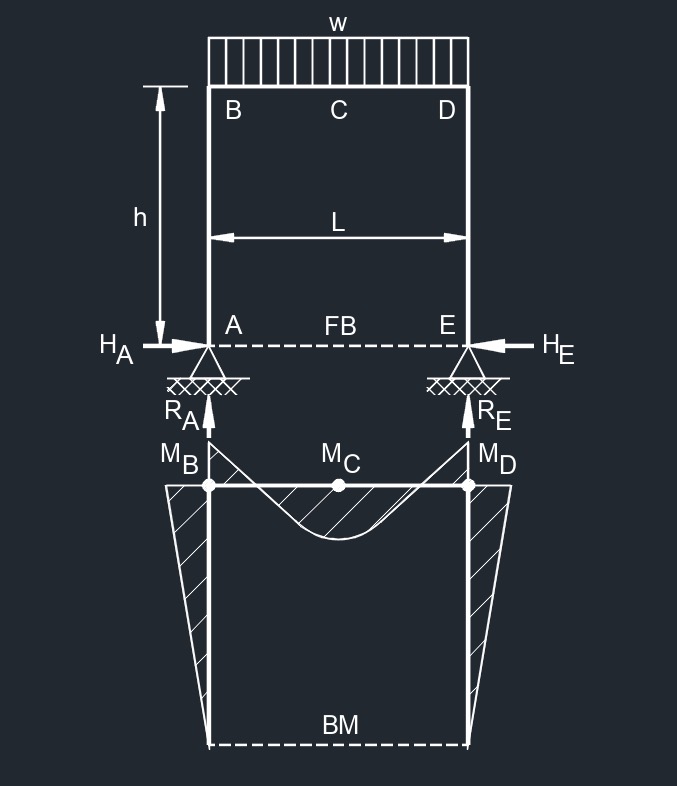3fpbe 4Top Uniformaly Distributed Load

 

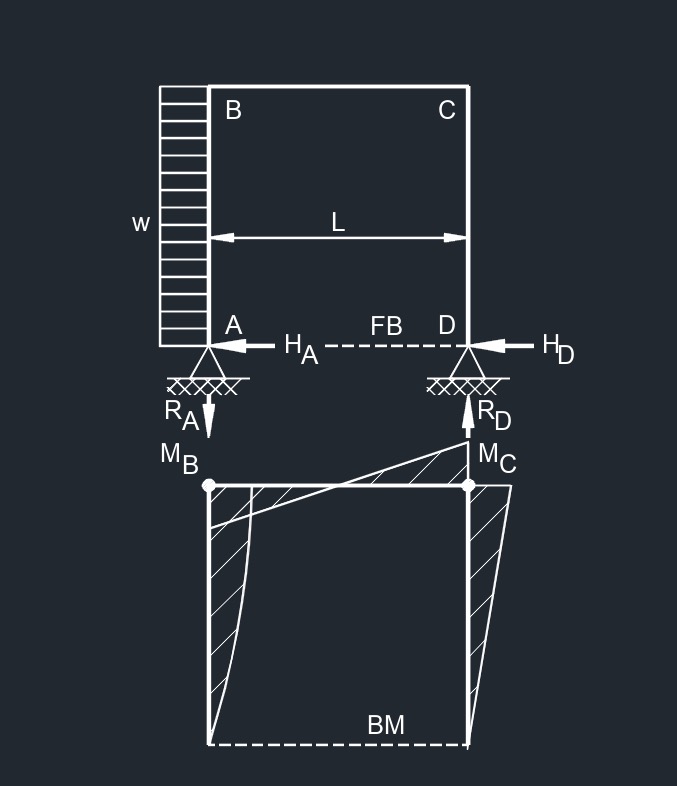3fpbe 5Side Uniformaly Distributed Load

 

 

 

 

 

 

 

Three Member Frame - Pin/Roller

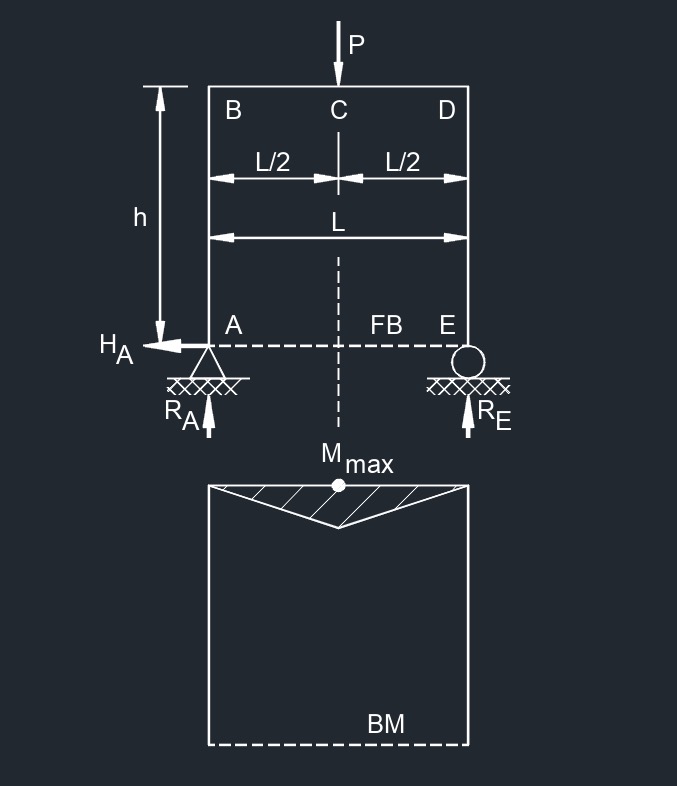3fpr 1Center Point Load 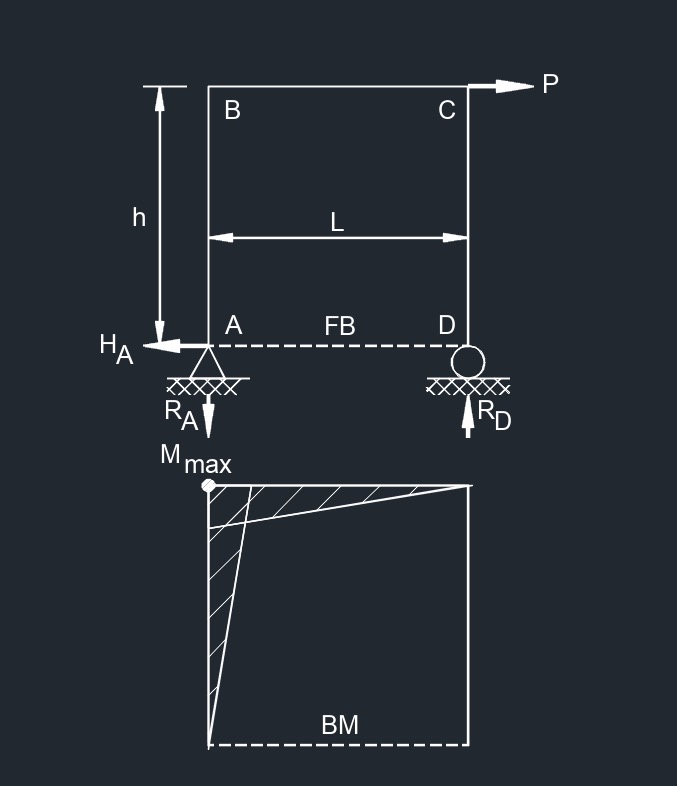3fpr 2ASide and Top Point Load 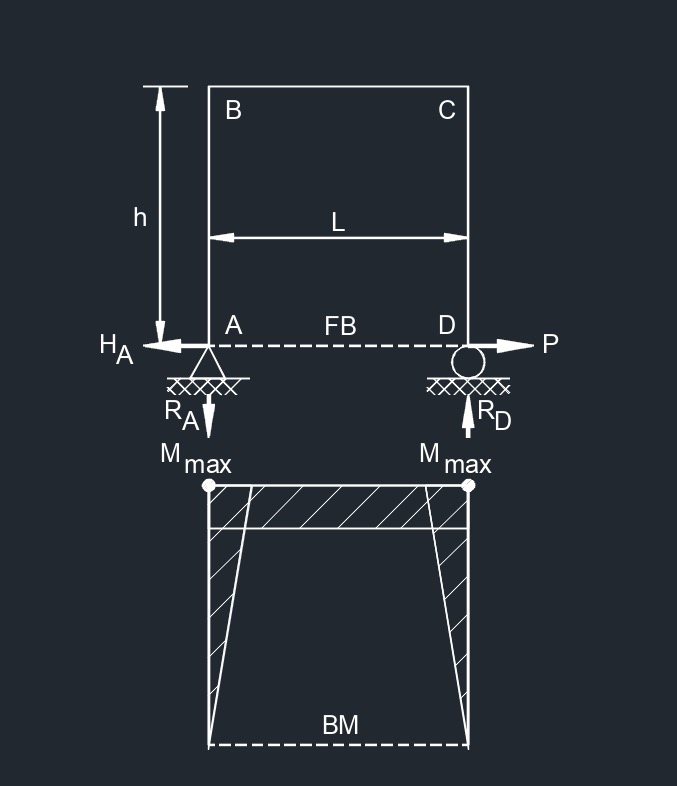3fpr 3Side and Bottom Point Load 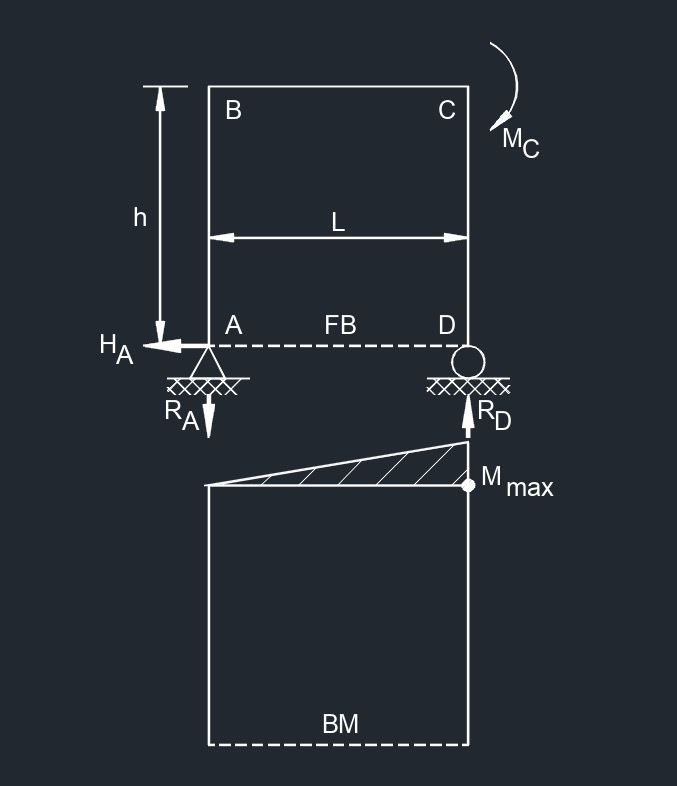3fpr 4Side and Top Bending Moment

 

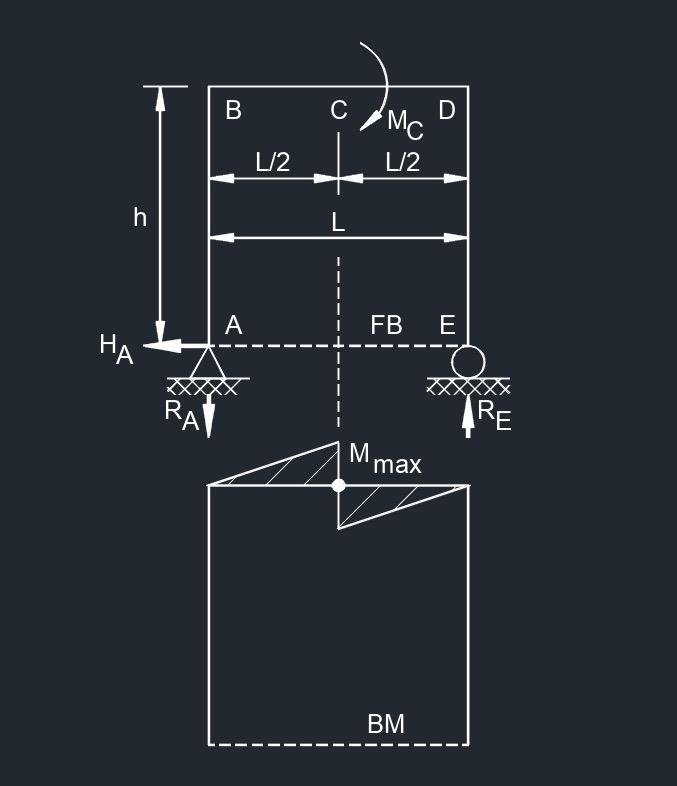3fpr 5Central Bending Moment 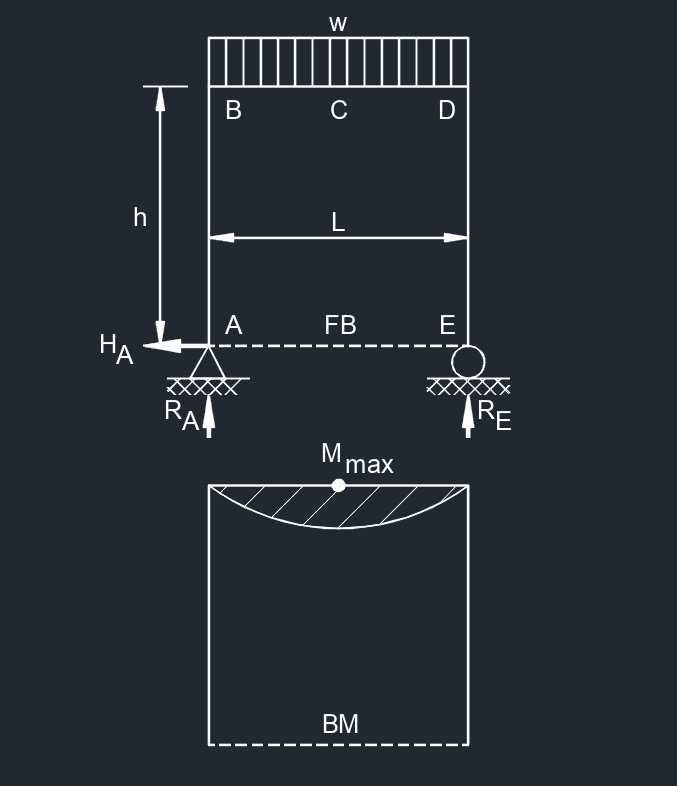3fpr 6Top Uniformaly Distributed Load 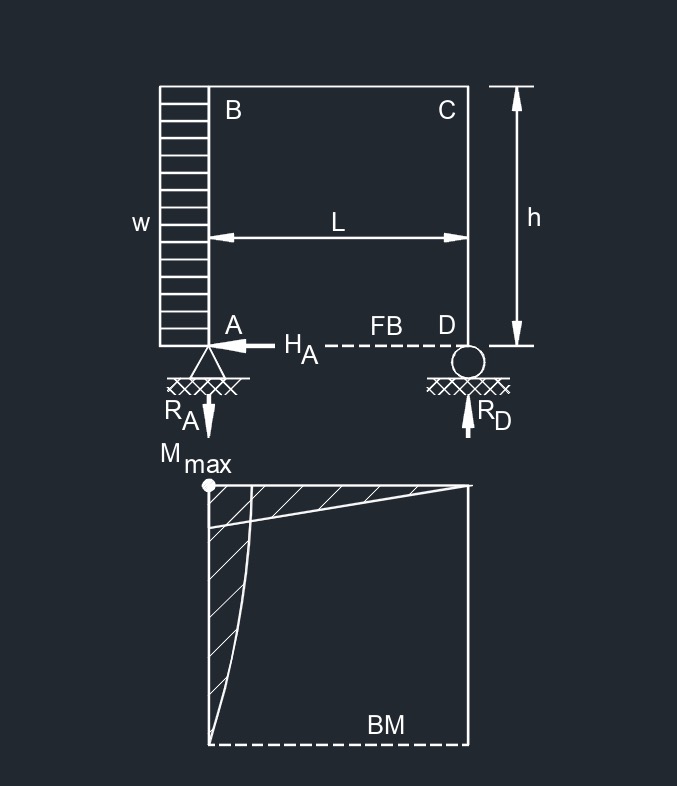3fpr 7Side Uniformaly Distributed Load 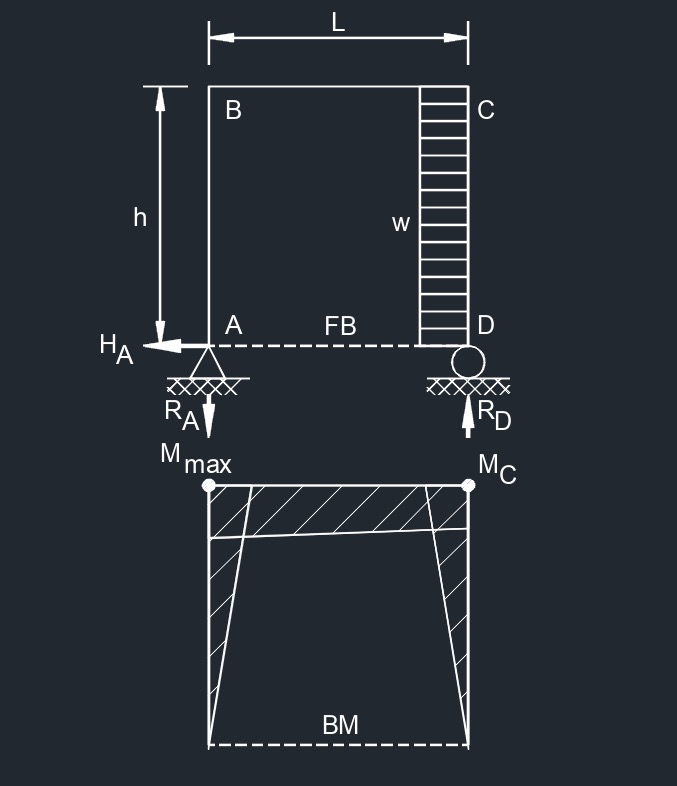3fpr 8Outer Side Uniformaly Distributed Load

 

 

 

 

 

 

 

 

Nomenclature, Symbols, and Units for Frame Supports
Symbol Greek Symbol Definition English Metric SI Value
\(\Delta\) Delta deflection or deformation \(in\) \(mm\) \(mm\) -
\(h\) - height of frame \(in\) \(mm\) \(mm\) -
\(x\) - horizontal distance from reaction point \(in\) \(mm\) \(mm\) -
\(H\) - horizontal reaction load at bearing point \(lbf\) \(N\) \(kg-m-s^{-2}\) -
\(I_h\) - horizontal member second moment of area (moment of inertia) \(in^4\) \(mm^4\) \(mm^4\) -
\(w\) - load per unit length \(\large{\frac{lbf}{in}}\) \(\large{\frac{N}{m}}\) \(N-m^{-1}\)  -
\(M\) - maximum bending moment \(lbf-in\) \(N-mm\) \(N-mm\)  -
\(\lambda\) lambda modulus of elasticity \(\large{\frac{lbf}{in^2}}\) \(MPA\) \(N-mm^{-2}\)  -
\(A, B, C, D, E\) - point of intrest on frame - - -  -
\(L\) - span length under consideration \(in\) \(mm\) \(mm\)  -
\(P\) - total concentrated load \(lbf\) \(N\) \(kg-m-s^{-2}\) -
\(I_v\) - vertical member second moment of area (moment of inertia) \(in^4\) \(mm^4\) \(mm^4\)  -
\(R\) - vertical reaction load at bearing point \(lbf\) \(N\) \(kg-m-s^{-2}\) -

 

Piping Designer Logo Slide 1