Article Links |
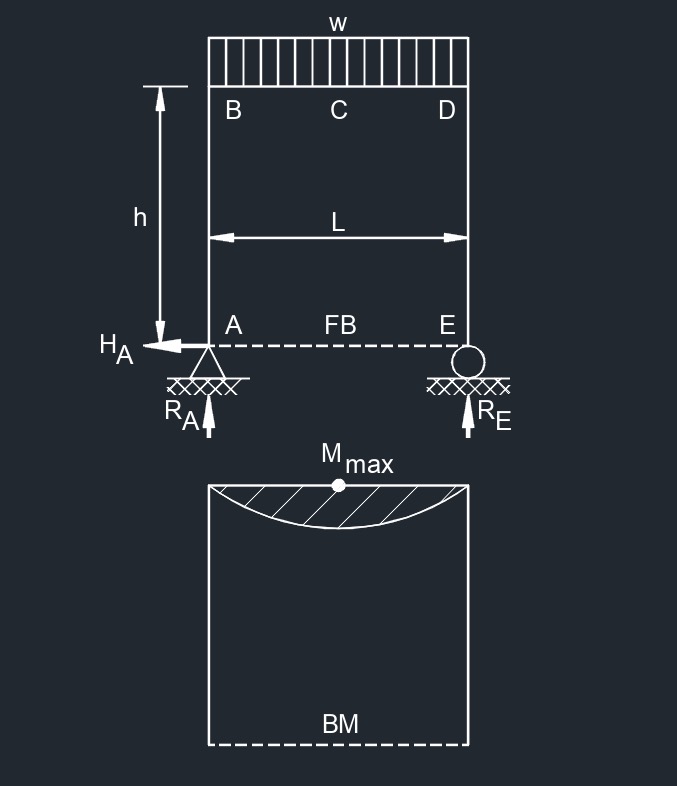
Three Member Frame - Pin/Roller Top Uniformly Distributed Load formulas
| \(\large{ R_A = R_E = \frac{w\;L}{2} }\) | |
| \(\large{ H_A = 0 }\) | |
| \(\large{ M_{max} \;(at \; C) = \frac{w\;L^2}{8} }\) | |
| \(\large{ \Delta_{Ex} = \frac{w\;h\;L^3}{12 \; \lambda \; I} }\) |
Where:
| Units | English | Metric |
| \(\large{ \Delta }\) = deflection or deformation | \(\large{in}\) | \(\large{mm}\) |
| \(\large{ h }\) = height of frame | \(\large{in}\) | \(\large{mm}\) |
| \(\large{ H }\) = horizontal reaction load at bearing point | \(\large{lbf}\) | \(\large{N}\) |
| \(\large{ I_h }\) = horizontal member second moment of area (moment of inertia) | \(\large{in^4}\) | \(\large{mm^4}\) |
| \(\large{ I_v }\) = vertical member second moment of area (moment of inertia) | \(\large{in^4}\) | \(\large{mm^4}\) |
| \(\large{ w }\) = load per unit length | \(\large{\frac{lbf}{in}}\) | \(\large{\frac{N}{m}}\) |
| \(\large{ M }\) = maximum bending moment | \(\large{lbf-in}\) | \(\large{N-mm}\) |
| \(\large{ \lambda }\) (Greek symbol lambda) = modulus of elasticity | \(\large{\frac{lbf}{in^2}}\) | \(\large{PA}\) |
| \(\large{ A, B, C, D, E }\) = point of intrest on frame | - | - |
| \(\large{ L }\) = span length under consideration | \(\large{in}\) | \(\large{mm}\) |
| \(\large{ R }\) = vertical reaction load at bearing point | \(\large{lbf}\) | \(\large{N}\) |
diagrams
- Bending moment diagram (BMD) - Used to determine the bending moment at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
- Free body diagram (FBD) - Used to visualize the applied forces, moments, and resulting reactions on a structure in a given condition.
- Shear force diagram (SFD) - Used to determine the shear force at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
- Uniformly distributed load (UDL) - A load that is distributed evenly across the entire length of the support area.
